L'acétone ou propanone $(CH_{3}-CO-CH_{3})$, liquide à température ordinaire, est un solvant très utilisé dans l'industrie et en laboratoire.

 

On l'utilise en particulier comme dissolvant de colles ou pour le dégraissage industriel. 

 

L'acétone permet également de fabriquer des matières plastiques et des médicaments.

 

Un laborantin met au point un protocole expérimental permettant de synthétiser la propanone et de suivre l'évolution de la réaction de synthèse au cours du temps.

 

1.1 Il réalise la synthèse de la propanone par oxydation du propan-$2$-ol par l'ion dichromate $\left(Cr_{2}O_{7}^{2^{+}}\right)$ en milieu acide.

 

1.1.1 Écrire le groupement fonctionnel de la propanone et dire à quelle famille elle appartient. $(0.5\;pt)$

 

1.1.2 Montrer à partir des demi-équations des couples mis en jeu que l'équation-bilan de la réaction chimique s'écrit : 

 

$3C_{3}H_{8}O+Cr_{2}O_{7}^{2^{-}}+8H^{+}\quad\rightarrow\quad 3C_{3}H_{6}O+2Cr^{3^{+}}+7H_{2}O$ $(0.75\;pt)$

 

Couples oxydants/réducteurs mis en jeu :

 

$\bullet$ couple ion dichromate/ion chrome (III) $\left(Cr_{2}O_{7}^{2^{-}}/Cr^{3^{+}}\right)$

 

$\bullet$ couple propanone/propan-$2$-ol $\left(C_{3}H_{6}O/C_{3}H_{8}O\right)$

 

1.2 Pour suivre l'évolution, au cours du temps, de la quantité de matière $(n)$ de propanone formée, le laborantin introduit dans un erlenmeyer un volume $V_{1}=50\;mL$ de solution de dichromate de potassium de concentration molaire $C_{1}=2\cdot 10^{-1}mol\cdot L^{-1}$, un volume $V_{a}=49\;mL$ d'une solution d'acide sulfurique concentrée et un volume $V=1\;mL$ de propan-$2$-ol. 

 

Le mélange est ensuite immédiatement réparti équitablement dans $10$ tubes à essais.

 

1.2.1 Calculer les quantités de matière initiales $n_{01}$ d'ions dichromate et $n_{02}$ de propan-$2$-ol présents dans un tube à essais. 

 

En déduire le réactif limitant. $(0.75\;pt)$

 

Données : 

 

masse volumique du propan-$2$-ol $\rho=0.785\;g/mL$ ; 

 

masse molaire $M=60.0\;g/mol.$

 

1.2.2 Une méthode appropriée de dosage a permis de déterminer la quantité de matière $n_{r}$ d'ions dichromate restant dans un tube à l'instant $t.$

 

Montrer que la quantité de matière, $n$, de propanone formée à l'instant $t$ s'exprime par :

 

$n(mmol)=3(1-n_{r})$ avec $n_{r}$ en mmol. $(0.5\;pt)$

 

1.2.3 Reproduire le tableau ci-dessous sur la copie et le compléter. $(0.25\;pt)$

$$\begin{array}{|c|c|c|c|c|c|c|c|c|c|c|} \hline t(min)&0&1&2&3&4&6&10&15&20&25\\ \hline n_{r}(mmol)&1.00&0.92&0.87&0.83&0.81&0.78&0.74&0.72&0.71&0.71\\ \hline n(mmol)& & & & & & & & & & \\ \hline  \end{array}$$

 

1.2.4 Tracer le graphe $n=f(t).$

 

Échelle : $1\;cm\rightarrow 2\;min$ ; $1\;cm\rightarrow 0.1\;mmol$ $(0.50\;pt)$

 

1.2.5 Déterminer les vitesses instantanées de formation aux dates $t_{1}=3\;min$ et $t_{2}=15\;min.$

 

Justifier brièvement l'évolution de cette vitesse. $(0.75\;pt)$

Plus on est âgé, moins les protéines sont assimilées et moins bien utilisées par le corps.

 

En ajoutant de la leucine à l'alimentation et aux protéines, le corps retrouve sa capacité d'assimilation et d'utilisation des protéines. 

 

On peut trouver la leucine en quantité notable dans les arachides, le riz, le thon, le filet de bœuf...

 

Dans ce qui suit, on se propose d'étudier la structure de la leucine et quelques-unes de ses propriétés.

 

2.1 La leucine est un acide $a$-aminé de formule semi-développée :

 

 

 

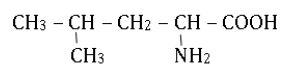
2.1.1 Donner le nom de la leucine dans la nomenclature officielle. 

 

La molécule de leucine est-elle chirale ? 

 

Justifier la réponse. $(0.75\;pt)$

 

2.1.2 La $D$-leucine présente des propriétés antalgiques utilisées en médecine dans le traitement de la douleur. 

 

La $L$-leucine a une saveur sucrée et elle est utilisée comme additif alimentaire.

 

Écrire les représentations de Fischer de la $L$-leucine et de la $D$-Leucine. $(0.5\;pt)$

 

2.2 Dans la solution aqueuse de la leucine il existe, entre autres espèces chimiques, un ion dipolaire appelé amphion ou zwittérion.

 

2.2.1 Écrire la formule semi-développée de cet amphion. $(0.25\;pt)$

 

2.2.2 L'amphion intervient dans deux couples acide/base. 

 

Écrire ces couples acide/base. $(0.5\;pt)$

 

2.3 On fait réagir la leucine avec un acide $\alpha$-aminé $A$ de formule $R-CH(NH_{2})-COOH$ où $R$ est un radical alkyle. 

 

On obtient un dipeptide de masse molaire $202\;g\cdot mol^{-1}.$

 

2.3.1 Déterminer la formule semi-développée de l'acide $\alpha$-aminé $A$ puis le nommer. $(0.5\;pt)$

 

2.3.2 Écrire les formules semi-développées des dipeptides que l'on peut obtenir en faisant réagir une molécule de leucine et une molécule de l'acide $\alpha$-aminé $A.$ $(0.5\;pt)$

 

2.3.3 On veut synthétiser le dipeptide pour lequel la leucine est l'acide $\alpha$-aminé $N$-terminal. 

 

Préciser les différentes étapes de cette synthèse (il n'est pas demandé d'écrire les équations de réaction de ces étapes). $(01\;pt)$

 

$M(C)=12\;g\cdot mol^{-1}$ ; 

 

$M(O)=16\;g\cdot mol^{-1}$ ; 

 

$M(H)=1\;g\cdot mol^{-1}$ ; 

 

$M(N)=14\;g\cdot mol^{-1}.$

La sonde spatiale $SOHO$ (Solar and Heliospheric Observatory) est un satellite qui a été mis en orbite par la fusée ATLAS II. 

 

Elle a pour mission d'étudier la structure interne du soleil, la chaleur de son atmosphère et les origines du vent solaire.

 

Dans ce qui suit, on étudie le mouvement de la sonde.

 

3.1 Au décollage, le mouvement de la fusée ATLAS II est étudié dans le référentiel terrestre supposé galiléen. 

 

La fusée et son équipement (y compris la sonde) ont une masse $M=850$ tonnes supposée constante durant le décollage. 

 

La force de poussée $\overrightarrow{F}$ générée par les propulseurs de la fusée a une intensité égale à $16\cdot10^{6}N$ durant la phase de décollage.

 

3.1.1 Déterminer la valeur algébrique de l'accélération du centre d'inertie de la fusée durant le décollage sachant que le repère d'espace choisi est l'axe vertical $(OZ)$ orienté vers le haut et que le centre d'inertie de la fusée est initialement confondu avec l'origine $O.$ $(0.5\;pt)$

 

3.1.2 Établir la loi horaire de son altitude $z(t)$ durant cette phase.

 

Calculer l'altitude à la date $t=15\;s.$ $(0.5\;pt)$

 

3.2 Le Soleil, de centre $S$ et de masse $M_{S}$ et la Terre de centre $T$ et de masse $M_{T}$, sont considérés comme des astres présentant une répartition de masse à symétrie sphérique.

 

 

 

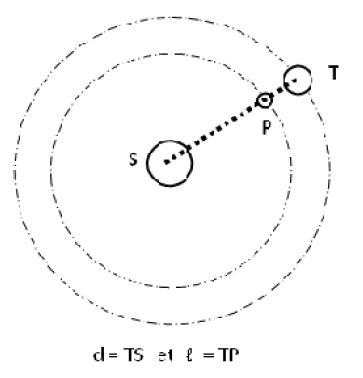
On admet que la Terre décrit autour du Soleil, d'un mouvement uniforme, une orbite circulaire de centre $S$ et de rayon $d.$

 

Sa période de révolution est de $365.25$ jours.

 

3.2.1 On suppose que la Terre ne subit que l'action du Soleil

 

Exprimer la vitesse angulaire de la Terre sur son orbite en fonction de $G$, $M_{s}$ et $d.$ $(0.5\;pt)$

 

3.2.2 En déduire la valeur de la masse $M_{s}$ du Soleil. $(0.25\;pt)$

 

3.2.3 Le satellite $SOHO$, assimilé à un point matériel $P$ de masse $m$, est placé à un endroit très particulier du système solaire, le point de Lagrange $L_{1}$, situé à la distance $\ell$ du centre de la Terre. 

 

Il décrit autour du Soleil, d'un mouvement uniforme, une orbite circulaire de rayon $b=d-\ell.$

 

Les centres de $S$, $P$ et $T$ sont constamment alignés.

 

3.2.3.1. A quelle vitesse angulaire $SOHO$ tourne-t-il autour du Soleil ?

 

Justifier la réponse. $(0.25\;pt)$

 

3.2.3.2. Faire l'inventaire des forces qui agissent sur le satellite $P.$ 

 

Les représenter sur un schéma. $(0.5\;pt)$

 

3.2.3.3 En appliquant le théorème du centre d'inertie au satellite et en tenant compte du résultat obtenu à la question 3.2.1, établir la relation entre $d$, $\ell$ et le rapport des masses $\dfrac{M_{T}}{M_{S}}$ $(0\;5\;pt)$

 

3.2.3.4. Tenant compte du fait que le point de Lagrange $L_{1}$ est situé beaucoup plus près du centre de la Terre que de celui du Soleil, on peut faire l'approximation

$\dfrac{\ell}{d}<<1.$

 

Établir alors la relation :$$\left(\dfrac{\ell}{d}\right)^{3}=\dfrac{M_{T}}{3M_{S}}$$

 

Calculer la distance $\ell$ situant le point de Lagrange à la Terre. $(0.5\;pt)$

 

3.3 Quel est l'avantage d'un satellite comme $SOHO$ par rapport à des observatoires terrestres ? $(0.25\;pt)$

 

3.4 D'après un article extrait d'un hebdomadaire de vulgarisation scientifique « SOHO est le premier observatoire spatial à être placé à un endroit très particulier du système solaire le point de Lagrange $L_{1}$ du nom d'un mathématicien français qui en a découvert l'existence... 

 

A cet endroit précis où l'attraction du Soleil équilibre très exactement l'attraction de la Terre, le satellite spatial peut observer le Soleil $24h$ sur $24$ ».

 

L'information fournie par cet article selon laquelle SOHO est situé à un endroit précis où l'attraction du Soleil équilibre très exactement l'attraction de la Terre est-elle compatible avec le mouvement circulaire uniforme de SOHO autour du Soleil ? 

 

Justifier la réponse. $(0.25\;pt)$

masse de la Terre $M_{T}=5.98\cdot10^{24}kg$ ; 

 

distance Terre-Soleil $d=1.50\csc10^{8}km$ ;

 

Constante de gravitation $G=6.67\;10^{-11}N\cdot m^{2}\cdot kg^{-2}$ ;

 

intensité du champ de gravitation terrestre au sol, $g_{0}=9.80\;m\cdot s^{-2}.$

Il n'est pas demandé de rendre les documents $1$,$2$ et $3$ de la page $4$ avec la feuille de copie.

 

Toutefois on expliquera succinctement l'exploitation faite de ces documents pour répondre aux questions.

 

Pour étudier le phénomène de résonance au laboratoire, un groupe d'élèves réalise un circuit $(R\;,\ L\;,\ C)$ série. 

 

Pour cela, ils disposent d'un $GBF$ qui fournit une tension alternative sinusoïdale de fréquence $N$ réglable, un conducteur ohmique de résistance $R=50\omega$, un condensateur de capacité $C=5\mu F$, une bobine de résistance $r$ et d'inductance $L.$

 

4.1 Les élèves visualisent sur la voie $Y_{1}$ de l'oscilloscope la variation au cours du temps de la tension $u_{G}(t)$ aux bornes du générateur et sur la voie $Y_{2}$ la variation au cours du temps de la tension $u_{G}(t)$ aux bornes du résistor.

 

4.1.1 Faire le schéma du montage qu'ils ont réalisé en y indiquant clairement les connexions à faire à l'oscilloscope pour visualiser $u_{G}(t)$ et $u_{R}(t).$ $(0.5\;pt)$

 

4.1.2 Expliquer pourquoi la variation de la tension $u_{R}(t)$ leur donne en même temps l'allure de la variation de l'intensité $i(t)$ du courant dans le circuit. $(0.25\;pt)$

 

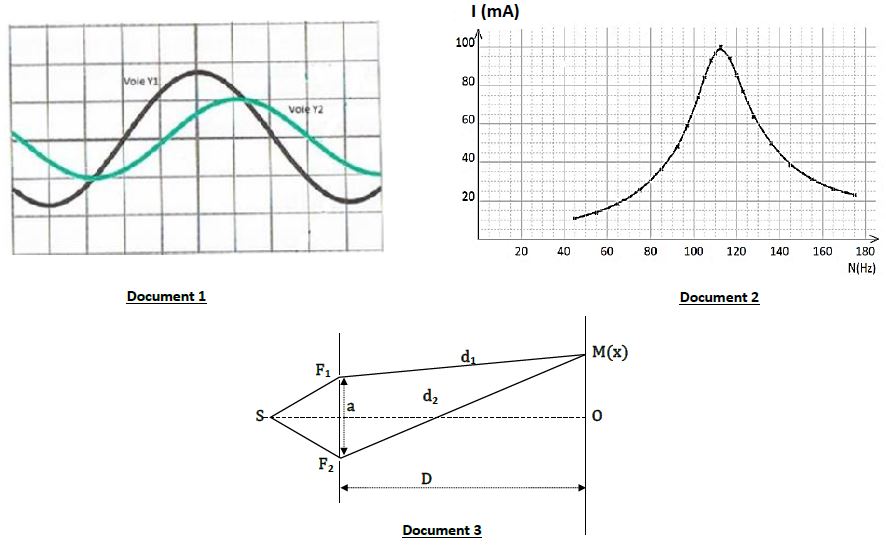
4.2 Sur l'écran de l'oscilloscope, sont observés les oscillogrammes reproduits sur le document $1$ avec les réglages suivants : 

 

Sensibilité verticale voie $Y_{1}$ : $5V/div$ ; 

 

voie $Y_{2}$ : $0.5V/div$ ;

 

Sensibilité horizontale : $1\;ms/div.$

 

4.2.1 Déterminer :

 

$\bullet$ la fréquence $N$ de la tension délivrée par le générateur ;

 

$\bullet$ la tension maximale $U_{m}$ aux bornes du générateur ;

 

$\bullet$ l'intensité maximale $I_{m}$ du courant. $(01.25\;pt)$

 

4.2.2 Déterminer le déphasage de la tension aux bornes du générateur sur l'intensité du courant. $(0.5\;pt)$

 

4.2.3 Sur un schéma représentant l'aspect de l'écran, montrer comment se positionnerait la courbe $1$

 

visualisée sur la voie $(Y_{1})$ par rapport à la courbe $2$ visualisée sur la voie $(Y_{2})$ à la résonance d'intensité (On tracera l'allure des deux courbes). $(0.25\;pt)$

 

4.3 En maintenant la tension maximale aux bornes du générateur constante, les élèves ont fait varier la fréquence $N$ du $GBF$ et relevé l'intensité efficace $I$ du courant à l'aide d'un ampèremètre.

 

Les mesures ainsi réalisées leur ont permis de tracer la courbe $I=f(N)$ du document $2.$

 

4.3.1 Déterminer graphiquement la fréquence $N_{0}$ et l'intensité efficace $I_{0}$ à la résonance d'intensité

 

En déduire l'inductance $L$ de la bobine. $(0.75\;pt)$

 

4.3.2 Déterminer la bande passante des fréquences et le facteur de qualité.

 

Donner la signification physique du facteur de qualité. $(0.5\;pt)$

Les fentes de Young permettent, entre autres dispositifs, de mettre en évidence le phénomène d'interférences lumineuses.

 

Au cours d'une séance de travaux pratiques, des élèves doivent établir expérimentalement la relation entre la distance $a$ qui sépare les fentes de Young et l'interfrange $i.$ 

 

Pour ce faire, ils réalisent le dispositif interférentiel de Young. 

 

La source laser $S$, équidistante des deux fentes, produit une radiation lumineuse de longueur d'onde $\lambda.$

 

L'écran, parallèle au plan des fentes, est placé à une distance $D=1.000\;m$ dudit plan.

 

La distance $a$ entre les fentes est réglable (document 3).

 

Une fois le protocole validé par le professeur, les élèves mesurent l'interfrange $i$ pour différentes valeurs de la distance $a$ entre les fentes et calculent le produit $i\cdot a$

 

Les résultats obtenus sont consignés dans le tableau ci-dessous.

$$\begin{array}{|c|c|c|c|c|} \hline a\left(10^{-3}m\right)&0.10&0.20&0.30&0.40\\ \hline i\left(10^{-3}m\right)&6.5&3.3&2.2&1.6\\ \hline i\cdot a& & & &\\ \hline \end{array}$$

 

5.1 Expliquer qualitativement le phénomène d'interférences lumineuses observé sur l'écran.

 

Quel caractère de la lumière l'expérience d'interférences lumineuses met en évidence ? $(0.5\;pt)$

 

5.2 Pour un point $M$ de l'écran, d'abscisse $x$, la différence de marche est donnée par :

 

$\delta=d_{2}-d_{1}=\dfrac{a_{x}}{D}.$ 

 

Quelle condition doit remplir la différence de marche pour que le point $M$ soit le milieu d'une frange obscure ? 

 

Exprimer dans ce cas l'abscisse $x$ du point $M$ en fonction de $\lambda$, $D$, $a$ et $k$ (entier naturel). $(0.5\;pt)$

 

5.3 Définir l'interfrange. 

 

Établir son expression en fonction de $\lambda$, $D$ et $a.$ $(0.5\;pt).$

5.4

5.4.1 Reproduire le tableau ci-dessus et le compléter. 

 

Vérifier que l'interfrange $i$ est inversement proportionnel à la distance $a$ qui sépare les fentes. 

 

Ce résultat est-il en accord avec la réponse fournie à la question 5.3 ? $(01.25\;pt)$

 

5.4.2 En déduire la valeur de la longueur d'onde $\lambda$ de la radiation émise par le laser $(0.5\;pt).$

 

5.5 Les élèves éclairent ensuite, avec le laser, une cellule photoélectrique. 

 

Le travail d'extraction est $W_{0}=1.9\;eV.$ 

 

Quel phénomène observent-ils ? 

 

Justifier la réponse. 

 

Préciser le caractère de la lumière mis en évidence dans ce cas. $(0.75\;pt)$

 

Données : 

 

$1eV=1.6\cdot10^{-19} J$ ; 

 

constante de Planck $h=6.62\cdot10^{-34}J\cdot s$ ;

 

vitesse de la lumière dans le vide $C=3.000\cdot10^{8}m\cdot s^{-1}$