Bac Physique Chimie 1er Groupe S1 S3 2011

L'asparagine est un composé organique exigé par le système nerveux pour maintenir l'équilibre.

 

Ce composé augmente la résistance à la fatigue, intensifiant de ce fait la vigueur des athlètes.

 

Les symptômes d'insuffisance de l'asparagine peuvent mener à la confusion, aux maux de tête, à la dépression, à l'irritabilité ou, dans des cas extrêmes, à la psychose.

 

C'est un composé que le corps peut fabriquer dans le foie. 

 

On le trouve aussi dans les produits laitiers, l'œuf, la viande (porc) et la volaille.

 

La molécule d'asparagine a pour formule :

 

 

 

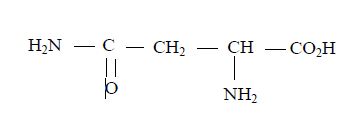
1.1 Cette molécule est-elle chirale ? 

 

Justifier la réponse. $(0.5\;point)$

 

1.2 Quelles fonctions chimiques possède l'asparagine ? $(0.5\;point)$

 

1.3 L'asparagine peut-être synthétisée à partir de l'acide aspartique de formule :

 

 

 

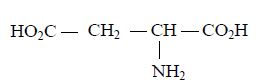
Préciser le composé (formule et nom) qu'il faut faire réagir avec cet acide pour préparer l'asparagine.

 

Écrire les équations des réactions mises en jeu dans cette préparation. $(0.5\;point)$

 

1.4 La décarboxylation de l'acide aspartique donne, entre autres, une molécule d'acide $\alpha$ aminé chirale $A.$

 

1.4.1 Écrire l'équation de la réaction de décarboxylation et nommer la molécule $A.$ $(0.5\;point)$

 

1.4.2 Donner les représentations spatiales des deux énantiomères de $A$ ainsi que leurs représentations de Fisher. $(01\;point)$

L'eau de Javel est une solution équimolaire d'hypochlorite de sodium $\left(Na^{+}+ClO^{-}\right)$ et de chlorure de sodium. 

 

A la maison, elle est surtout utilisée comme antiseptique ou comme décolorant dans le blanchissage. 

 

Elle doit être conservée en emballage opaque à l'abri de la chaleur pour éviter l'accélération de sa décomposition.

 

On se propose d'étudier la cinétique de la réaction de décomposition d'une eau de Javel catalysée par des ions cobalt $Co^{2+}.$

 

L'équation de cette réaction est : 

 

$2 ClO^{-}\quad\rightarrow\quad 2 Cl^{-}\quad+\quad O_{2}$

 

A une date $t=0s$, on dispose d'une eau de Javel catalysée par des ions $Co^{2+}$, de volume $V_{1}=100\;cm^{3}$, de concentration initiale en ions hypochlorite $\left[ClO^{-}\right]_{0}=2.6\cdot10^{-1} mol\cdot L^{-1}.$

 

Afin de suivre l'évolution de la réaction, on mesure à température et pression constantes, le volume $V(O_{2})$ de dioxygène dégagé au cours du temps, en $cm^{3}$, dans des conditions où le volume molaire est $V_{m}=22.4 L\cdot mol^{-1}.$

 

2.1 Montrer que la réaction de décomposition de l'eau de Javel est une réaction d'oxydo-réduction. $(0.5\;point)$

 

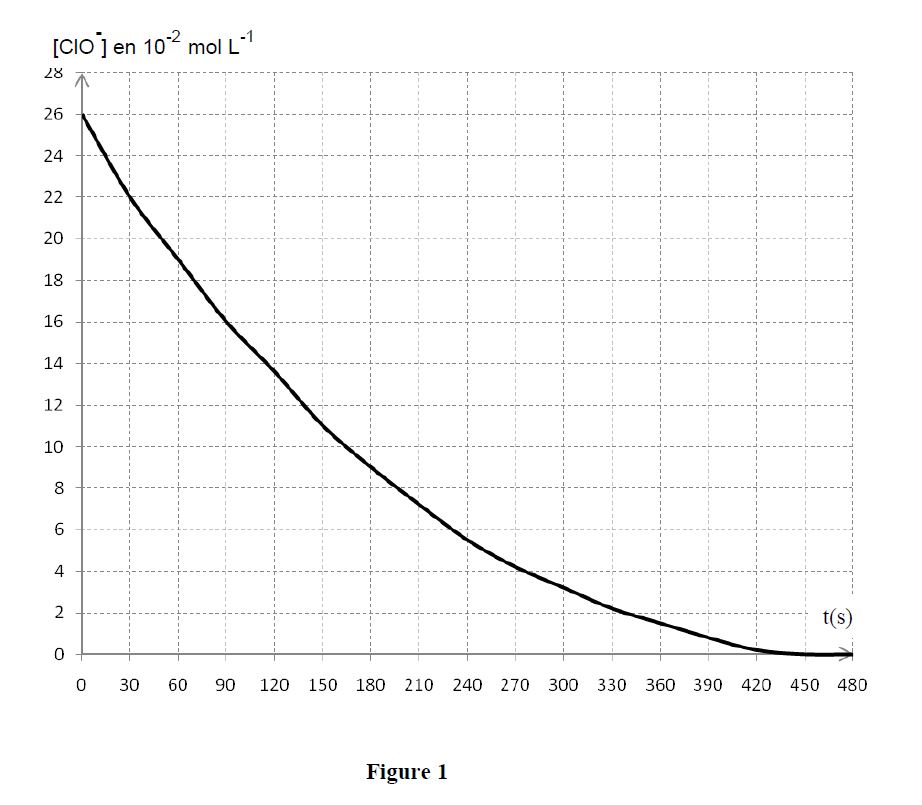
2.2 On détermine, à divers instants, le volume $V(O_{2})$ de dioxygène dégagé et on en déduit la concentration $\left[ClO^{-}\right]$ restant en fonction du temps ; on obtient la courbe $\left[ClO^{-}\right](t)=f(t)$ jointe en annexe (figure 1 de la page 5)..

 

2.2.1 Établir la relation qui permet de calculer la concentration $\left[ClO^{-}\right](t)$ en fonction de $\left[ClO^{-}\right]_{0}$, $V(O_{2})$, $V_{1}$ et $V_{m}.$ $(0.75\;point)$

 

2.2.2 Définir la vitesse volumique instantanée de disparition de l'ion hypochlorite à la date $t$ ; la calculer à $t=240s.$ $(0.5\;point)$

 

2.2.3 A quelle date le volume $V(O_{2})$ de dioxygène est-il égal à $200\;cm^{3}$ ? $(0.75\;point)$

 

2.3 Sur le graphe de la figure 1 de la page 5, à rendre avec la copie, tracer l'allure de la courbe représentant l'évolution de $\left[ClO^{-}\right]=f(t)$ en l'absence d'ions cobalt. 

 

Justifier la réponse. $(0.5\;point)$

L'Agence Internationale de l'Energie Atomique $(A.I.E.A)$ rapporte que lors de l'accident nucléaire survenu au Japon dans la préfecture de Fukushima le $14$ mars $2011$, des dépôts d'iode $131$ $\left(^{131}_{53}I\right)$ et de césium $137$ $\left(_{55}^{137}Cs\right)$ ont été détectés dès le $30$ mars $2011$ dans beaucoup d'autres préfectures du Japon.

 

L'iode $131$ et le césium $137$ sont des noyaux radioactifs $\beta^{-}$, de demi-vie respective $T_{I}=8.0$ jours et $T_{Cs}=30$ ans. 

 

Les riverains de la centrale sont ainsi exposés à une irradiation par inhalation ou par ingestion de ces noyaux du fait de la contamination de l'air atmosphérique et des aliments (eau, lait, légumes, poissons...). 

 

Le $06$ avril $2011$, un village environnant de la centrale de Fukushima s'est vu interdire l'usage de son eau pour les nourrissons à cause d'une concentration en iode de $100\;Bq$ par litre.

 

Données : 

 

masse de l'électron $m=0.00055\;u$ ; 

 

$1\;u=1.67\cdot10^{-27} kg=931.5\;MeV/C^{2}$

 

célérité de la lumière dans le vide $C=3\cdot10^{8} m\cdot s^{-1}$ ;

 

masse du noyau de césium : $m\left(^{137}_{55}Cs\right)=136.87692\;u$ ;

 

masse du noyau de baryum : $m\left(_{56}^{137}Ba\right)=136.87511\;u$

 

Extrait du tableau de classification :

$$\begin{array}{|c|c|c|c|c|} \hline _{52}Te&_{53}I&_{54}Xe&_{55}Cs&_{56}Ba\\ \hline \end{array}$$

 

3.1 On dit que la radioactivité naturelle est un phénomène aléatoire, spontané et inéluctable.

 

Expliquer brièvement chacun des termes soulignés ci-dessus. $(0.75\;point)$

 

3.2 Citer deux propriétés de la radioactivité $\beta^{-}.$ $(0.5\;point)$

 

3.3 Écrire les équations-bilan des réactions de désintégration de l'iode $131$ $\left(_{53}^{131}I\right)$ et du césium $137$ $\left(^{137}_{55}Cs\right).$ $(0.5\;point)$

 

3.4 Expliquer pourquoi on observe en même temps une émission de rayonnement $g.$

 

Écrire les équations des réactions nucléaires correspondantes. $(0.5\;point)$

 

3.5 Calculer, en $MeV$, l'énergie libérée par la désintégration d'un noyau de césium $137.$ $(0.5\;point)$

 

3.6 A un instant $t=0$, deux riverains $P_{1}$ et $P_{2}$ boivent, respectivement, l'un un litre d'eau contaminé à l'iode $131$ de concentration $100\;Bq$ par litre et, l'autre, un litre de lait de vache contaminé au césium $137$ de concentration $0.22\;Bq$ par litre.

 

3.6.1 Calculer le nombre de noyaux $N_{0}\left(_{53}^{131}I\right)$ d'iode $131$ présents à $t=0$ dans le litre d'eau consommé

 

par $P_{1}$ ainsi que le nombre de noyaux $N_{0}\left(_{55}^{137}Cs\right)$ de césium $137$ présents à $t=0$ dans le litre de lait consommé par $P_{2}.$

l'activité $A(t)$ d'un échantillon radioactif est liée au nombre N(t) de noyaux radioactifs présents par : 

 

$A(t)=\lambda N(t)$ $(0.5\;point)$

 

3.6.2 Rappeler l'expression liant $N$, $N_{0}$, $\lambda$ et $t$ respectivement, nombre de noyaux radioactifs à un instant quelconque $t$, nombre de noyaux radioactifs initial (à $t=0$), constante radioactive et instant quelconque. $(0.25\;point)$

 

3.6.3 Dans le tableau qui suit $N$ représente le nombre de noyaux radioactifs à la date $t.$

 

Recopier puis compléter le tableau. $(0.5\;point)$

$$\begin{array}{|c|c|c|c|c|} \hline t&0&8\text{ jours}&1\text{ an}&30\text{ ans}\\ \hline N\left(_{53}^{131}\right)&1.0\cdot10^{8}& & &\\ \hline N\left(^{137}_{55}Cs\right)&3.0\cdot10^{8}& & &\\ \hline \end{array}$$

 

3.6.4 En supposant que le danger lié à l'absorption d'un liquide contaminé est dù uniquement au nombre de noyaux radioactifs présents dans l'organisme, déduire de ce qui précède, lequel de $P_{1}$ ou $P_{2}$ est encore plus menacé un an après l'ingestion. $(0.5\;point)$

 

3.7 L'apport d'iode est essentiel à l'organisme humain qui le capte sous forme d'ions iodure au niveau de la glande thyroïde. 

 

L'isotope iode $127$ $\left(^{127}I\right)$ n'est pas radioactif contrairement à l'iode $131$ $\left(^{131}I\right)$ qui est particulièrement cancérigène. 

 

En cas de fuite radioactive on fait absorber le plus rapidement possible des comprimés d'iode $127$ sous forme d'iodure de potassium.

 

3.7.1 Justifier l'utilité de cette mesure. $(0.25\;point)$

 

3.7.2 Expliquer pourquoi, en cas d'absorption d'iode $131$ à un instant $t$, des noyaux d'iode continuent à irradier la thyroïde bien après cet instant. $(0.25\;point)$

Un sportif dans son véhicule démarre sans vitesse, en $D$, un mouvement sur une route rectiligne et horizontale (figure 2).

 

 

 

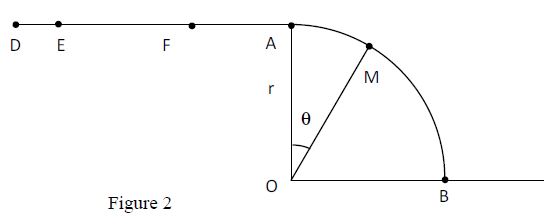
La masse totale (sportif et véhicule) est de $90\;kg.$

 

4.1 La phase de démarrage, considérée comme une translation rectiligne, a lieu sur un parcours $DE$ d'une longueur de $50\;m.$ 

 

Au point $E$, la vitesse atteint la valeur de $5\;m\cdot s^{-1}$

 

Pendant cette phase, la vitesse est proportionnelle au temps compté à partir de l'instant de démarrage.

 

4.1.1 Quelle est la nature du mouvement sur le parcours $DE$ ?

 

Justifier la réponse. 

 

Vérifier que l'accélération du mouvement sur ce parcours a pour valeur $0.25\;m\cdot s^{-2}$ $(0.5\;point)$

 

4.1.2 Établir l'équation horaire du mouvement sur ce parcours. $(0.25\;point)$

 

4.1.3 Calculer la durée de la phase de démarrage. $(0.25\;point)$

 

4.1.4 En admettant que le mouvement est dû à la résultante d'une force motrice constante parallèle au mouvement et d'une force de frottement constante, de norme égale au quart de la force motrice, de sens contraire au mouvement, calculer l'intensité de la force de frottement. $(0.5\;point)$

 

4.2 A partir du point $E$, le véhicule parcourt la distance $EF=1100\;m$ à la vitesse constante de $5\;m/s.$ 

 

A partir du point $F$, le sportif supprime la force motrice : 

 

le véhicule roule alors en roue libre et les frottements ont une valeur constante et égale à $7.5\;N$ sur le parcours $FA.$

 

Le véhicule parcourt la distance $FA$ et arrive au point $A$ avec une vitesse nulle...

 

42.1 Déterminer la distance $FA.$ $(0.5\;point)$

 

4.2.2 Calculer la durée totale du parcours du point $D$ au point $A.$ $(0.5\;point)$

 

4.3 Le véhicule aborde en $A$, sans vitesse initiale, une piste $AB$, parfaitement polie, de forme circulaire et de plan vertical. 

 

Sa position $M$ est repérée par l'angle $\theta=\left(\widehat{OA\;,\ OM}\right).$

 

4.3.1 Exprimer en fonction de $\theta$, $r$ et $g$ la vitesse du véhicule en $M$ et exprimer l'intensité de la réaction du plan en ce point en fonction de $m$, $g$ et $\theta.$ $(0.75\;point)$

 

4.3.2 Déterminer la valeur $\theta_{1}$ de l'angle  $\left(\widehat{OA\;,\ OM}\right)$ quand le véhicule quitte la piste. $(0.5\;point).$

 

4.3.3 Montrer que le véhicule quitte la piste quand son accélération est égale à l'accélération de la pesanteur $g.$ $(0.25\;point).$

Il n'est pas demandé de faire des applications numériques pour cet exercice.

 

5.1 Étude des dipôles $RC$, $RL$ et $RLC$ série.

 

On réalise successivement les circuits électriques correspondant aux schémas $1$ et $2.$

 

Dans le circuit correspondant au schéma $1$ sont associés, en série, un condensateur de capacité $C$ initialement déchargé, un conducteur ohmique de résistance $R$ et un générateur de f.e.m constante $E$ et de résistance négligeable.

 

 

 

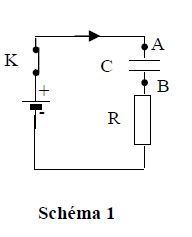
Dans le circuit correspondant au schéma $2$ sont associés, en série, une bobine d'inductance $L$, de résistance négligeable, un conducteur ohmique et un générateur identiques à ceux qui sont utilisés dans le premier circuit. 

 

 

 

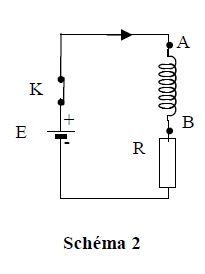
Le sens positif de l'intensité du courant $i$ est indiqué sur les schémas.

 

5.1.1 On ferme l'interrupteur $K$ de chacun des circuits et on visualise, à l'aide d'un oscillographe à mémoire, l'évolution de la tension $u_{R}$ aux bornes de chaque conducteur ohmique au cours du temps.

 

On observe les oscillogrammes $a$ et $b.$ 

 

 

 

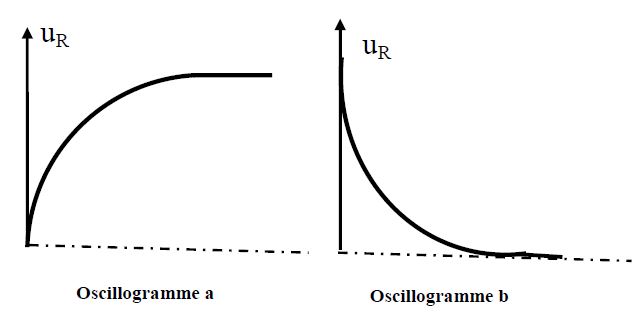
Le trait pointillé correspond à la trace du spot en l'absence de tension sur les deux voies.

 

5.1.1.1 Montrer que ces oscillogrammes visualisent les variations de l'intensité du courant électrique dans ces circuits. $(0.5\;point)$

 

5.1.1.2 Affecter à chaque schéma l'oscillogramme correspondant.

 

Justifier les réponses. $(0.5\;point)$

 

5.1.2 On considère le schéma $1.$ 

 

Lorsque le condensateur est chargé, le générateur est déconnecté du circuit et remplacé par une bobine d'inductance $L$ et de résistance négligeable et aussitôt l'interrupteur est fermé à une date prise comme origine des temps $t=0.$

 

5.1.2.1 Exprimer l'énergie $W_{0}$ initialement emmagasinée par le condensateur. $(0.25\;point)$

 

5.1.2.2 Préciser les échanges d'énergie qui ont lieu dans ce nouveau circuit et justifier que pour $t$ suffisamment grand, l'intensité du courant $i(t)\rightarrow 0.$

 

On considérera que la valeur de $R$ est telle que le régime est pseudo périodique $(0.75\;point)$

 

5.2 Étude du dipôle $RLC$ série en régime sinusoïdal forcé.

 

On associe maintenant, en série, un générateur de basse fréquence $(GBF)$, le conducteur ohmique de résistance $R$, la bobine d'inductance $L$, de résistance négligeable et le condensateur de capacité $C.$

 

Le générateur maintient entre ses bornes une tension sinusoïdale de valeur efficace $U$ constante et de fréquence réglable.

 

On fixe la fréquence à une valeur $N$ et on visualise sur l'écran d'un oscilloscope les tensions $u_{1}(t)$ aux bornes du conducteur ohmique à la voie $Y_{1}$ et $u_{2}(t)$ aux bornes du générateur à la voie $Y_{2}.$

 

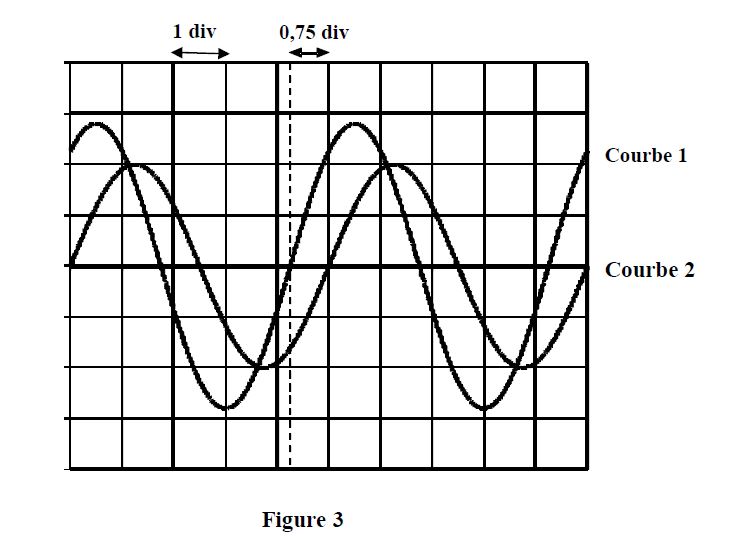
Les oscillogrammes de la figure 3 sont obtenus. 

 

Les réglages de l'oscilloscope (temps de balayage horizontal et sensibilités verticales des voies) ne sont pas donnés. 

 

On sait cependant que les deux voies ont la même sensibilité.

 

5.2.1 Schématiser le circuit et indiquer les connexions à l'oscilloscope. $(0.5 point).$

 

5.2.2 Affecter chaque courbe de la figure 3 à la voie correspondante. 

 

Justifier $(0.5\;point).$

 

5.2.3 Déterminer, en utilisant les oscillogrammes, le déphasage $\varphi$ de la tension $u_{2}(t)$ par rapport à l'intensité $i(t).$

 

En déduire l'expression de l'intensité instantanée $i(t)$ si $u_{2}(t)=U\sqrt{2}\cos(2\pi N)t.$ $(0.5\;point)$

 

 

 

5.3 Étude de la résonance d'intensité.

 

Dans le circuit précédent on choisit la fréquence $N$ de façon à réaliser la résonance d'intensité.

 

5.3.1 Montrer que la puissance électrique moyenne $P_{0}$ reçue par le dipôle constitué par le conducteur ohmique, la bobine et le condensateur est maximale.

 

Exprimer $P_{0}$ en fonction de $U$ et de $R.$ $(0.5\;point)$

 

5.3.2 Exprimer, en fonction du temps, l'énergie magnétique $W_{L}$ emmagasinée dans la bobine et l'énergie électrique $W_{C}$ emmagasinée dans le condensateur.

 

Montrer que l'énergie électrique totale $W_{t}$ emmagasinée dans le dipôle $R$, $L$, $C$ est constante.

 

Que devient donc à chaque instant l'énergie électrique reçue par le dipôle ? $(01\;point)$

 

Annexe à rendre avec la copie