Corrigé Bac pc 1er groupe S2-S2A-S4-S5 2017

 

1.1. .

1.1.1. Groupe fonctionnel de la propanone :

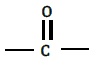
Famille des cétones.

 

1.1.2. Les demi-équations des couples oxydant-réducteurs :

 

$$C_{3}H_{6}O + 2H^{+} + 2e^{-}\ \leftrightarrows\ C_{3}H_{8}0$$

 

$$Cr_{2}O_{7}^{2-} + 14H^{+} + 6e^{-}\ \leftrightarrows\ 2Cr^{3+} + 7H_{2}0$$

 

Et l'équation bilan de la réaction :

 

$$\left.\begin{array}{rcl} 3\times[C_{3}H_{8}0&\longrightarrow&C_{3}H_{6}O + 2H^{+} + 2e^{-}]\\ Cr_{2}O_{7}^{2-} + 14H^{+} + 6e^{-}&\longrightarrow&2Cr^{3+} + 7H_{2}0\end{array}\right\rbrace$$

 

$$\Rightarrow\ 3C_{3}H_{8}0 + Cr_{2}O_{7}^{2-} + 8H^{+}\ \longrightarrow\ 3C_{3}H_{6}O + 2Cr^{3+} + 7H_{2}0$$

 

1.2.

 

1.2.1. Les quantités de matières initiales :

 

En ions $Cr_{2}O_{7}^{2-}\ :\ n_{01}=\dfrac{c_{1}V_{1}}{10}=1.00\;10^{-3}\;mol$

 

En propan-2-ol : $n_{02}=\dfrac{\rho.V_{2}}{10.M}=1.31\;10^{-3}\;mol$

 

Le réactif limitant : on a $\ \dfrac{n_{01}}{1}=1.00\;10^{-3}\;mol$

 

et $\ \dfrac{n_{02}}{3}=\dfrac{1.31\;10^{-3}}{3}=0.44\;10^{-3}\;mol$

 

$\Rightarrow\ \dfrac{n_{02}}{3}<\dfrac{n_{01}}{1}$

 

$\Rightarrow\ $ Le propan-2-ol est le réactif limitant.

 

1.2.2. Quantité de matière $n$ de propanone formée :

 

$\begin{array}{rcl}\dfrac{n}{3}&=&\dfrac{n_{Cr_{2}O_{7}^{2-}}(\text{réagi})}{1}\quad\text{or }\  n_{Cr_{2}O_{7}^{2-}}(\text{réagi})=n_{01}-n_{r}\\ \Rightarrow\ n&=&3(n_{01}-n_{r})\\ \Rightarrow\ n&=&3(1.10^{-3}-n_{r})\;,\quad\text{relation où } n\ \text{ et } n_{r} \text{ sont exprimés en } mol\end{array}$

 

On en déduit : $n=3(1-n_{r})$ avec $n\ $ et $\ n_{r}$ en $mmol$

 

1.2.3.

 

$$\begin{array}{|l|c|c|c|c|c|c|c|c|c|c|}\hline t(min)&0&1&2&3&4&6&10&15&20&25\\ \hline n_{r}(mmol)&1.00&0.92&0.87&0.83&0.81&0.78&0.74&0.72&0.71&0.71\\ \hline n(mmol)&0.00&0.24&0.39&0.51&0.57&0.66&0.78&0.84&0.87&0.87\\ \hline\end{array}$$

 

1.2.4. Courbe $n=f(t)$

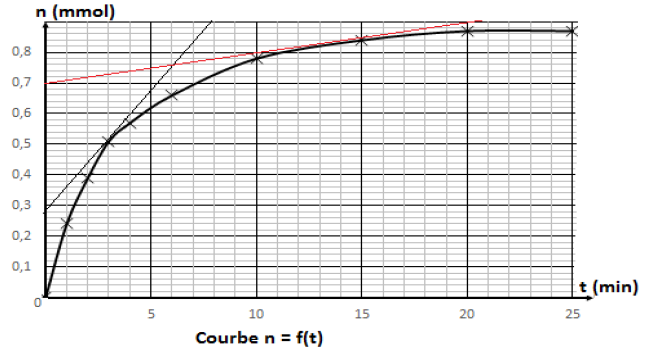
1.2.5. Vitesses de formation :

 

$$V(t_{1}=3\;min)\approx 7.57\;10^{-2}\;mmol.min^{-1}$$

 

$$V(t_{2}=15\;min)\approx 1.01\;10^{-2}\;mmol.min^{-1}$$

 

La vitesse de formation diminue au cours du temps car la quantité de matière des réactifs diminue.

2.1. .

 

2.1.1. Nom officiel de la leucine : acide 2-amino-4-méthylpentanoique

 

La molécule de leucine est chirale car elle possède un seul atome de carbone asymétrique. C'est l'atome de carbone marqué ci-dessous par un astérisque.

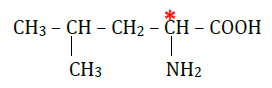
2.1.2. Représentations de Fischer :

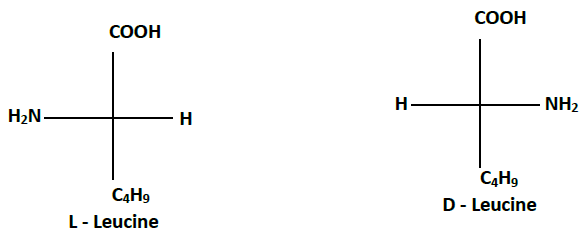
2.2. .

 

2.2.1. Formule de l'amphion :

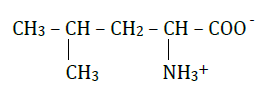
2.2.2. Les couples associés à l'amphion :

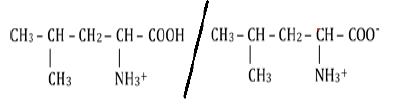
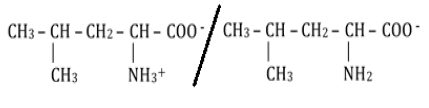
2.3. .

 

2.3.1.

 

$\begin{array}{lrcl} &M(A)+M(\text{Leucine)}&=&M(\text{(dipeptide)}+M(H_{2}O)\\ \Rightarrow&M(R)+205&=&202+18\\ \Rightarrow&M(R)&=&15\;g.mol^{-1}\end{array}$

 

$R$ est le radical $\text{méthyl}-CH_{3}.$

 

La formule semi-développée de $A$ est alors :

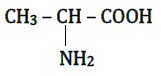
acide 2-amino propanoique

 

2.3.2 Formules semi-développées des deux dipeptides.

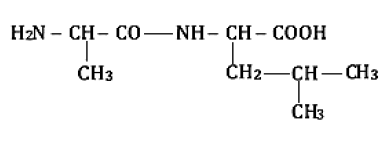
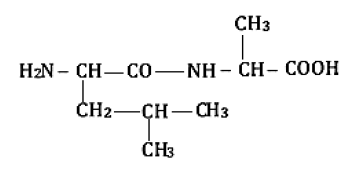
2.3.3 Les étapes de la synthèse :

 

$\lozenge\ $ Bloquer le groupe amino de la leucine et le groupe carboxyle de $A.$

 

$\lozenge\ $ Activer le groupe carboxyle de la leucine et le groupe amino de $A.$

 

$\lozenge\ $ Faire réagir les deux composés obtenus ci-dessus.

 

$\lozenge\ $ Après réaction, débloquer les groupements amino et carboxyle qui étaient bloqués.

3.1. .

 

3.1.1. Référentiel terrestre supposé galiléen

 

Système : fusée ;

 

Bilan des forces extérieures : poids $\vec{P}\ $ et force de poussée $\vec{F}$

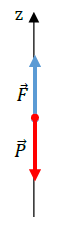
Théorème du centre d'inertie :  $\vec{P}+\vec{F}=M\vec{a}$

 

$\begin{array}{lrcl}\Rightarrow&F-P&=&M.a_{z}\\ \Rightarrow&a_{z}&=&\dfrac{F}{M}-g\end{array}$

 

A.N : $a_{z}=\dfrac{16\;10^{6}}{8.5\;10^{5}}-9.8=9.0\;m.s^{-2}$

 

3.1.2. Loi de variation $z(t)$ : 

 

$\begin{array}{lrcl} &a_{z}&=&\text{constante avec vitesse initiale nulle}\\ \Rightarrow&V_{z}&=&a_{z}t+C\quad\text{or à }\ t=0\;,\ V_{z}=V_{Oz}=0\;,\ \text{donc }C=0\\ \Rightarrow&V_{z}&=&a_{z}t\\ \\ \Rightarrow&z&=&\dfrac{1}{2}a_{z}t^{2}+C'\quad\text{or à }\ t=0\;,\ z=0\\ \\ \Rightarrow&z&=&\dfrac{1}{2}a_{z}t^{2}\end{array}$

 

$\boxed{z=4.51t^{2}}$

 

Altitude à la date $t=15\;s$ : 

 

$z=4.51\times(15)^{2}=1014\;m$

 

$\boxed{z=1.0\;km}$

 

3.2. .

 

3.2.1. Expression de la vitesse angulaire de la Terre :

 

Le mouvement de la Terre est circulaire est uniforme donc, l'accélération est normale

 

$\begin{array}{lrcl} \Rightarrow&a&=&a_{n}\ =\ \dfrac{G.M_{s}}{d^{2}}\quad\text{or }\ a_{n}=w^{2}d\\ \\ \Rightarrow&w^{2}d&=&\dfrac{G.M_{s}}{d^{2}}\\ \\ \Rightarrow&w^{2}&=&\dfrac{G.M_{s}}{d^{3}}\\  \\ \Rightarrow&w&=&\sqrt{\dfrac{G.M_{s}}{d^{3}}}\end{array}$

 

3.2.2. Valeur de la masse du Soleil :

 

$\begin{array}{lrcl} &w^{2}&=&\dfrac{G.M_{s}}{d^{3}}\\  \\ \Rightarrow&M_{s}&=&\dfrac{w^{2}.d^{3}}{G} \\ \\ & &=&\dfrac{4\pi^{2}d^{3}}{T^{2}G}\end{array}$

 

A.N : $M_{s}=2.10^{30}\;kg$

 

3.2.3. .

 

3.2.3.1. SOHO tourne d'un mouvement circulaire uniforme autour du Soleil comme la Terre ; les points $S\;,\ P\ $ et $\ T$ étant constamment alignés, SOHO a la même vitesse angulaire que la Terre : $$w_{\text{Soho}}=w_{T}$$

Cependant le rayon de sa trajectoire est $d-\ell.$

 

3.2.3.2. Forces qui agissent sur $P$ et leur représentation :

 

$\vec{F}_{s}$ = force de gravitation exercée par le Soleil sur $P.$

 

$\vec{F}_{T}$ = force de gravitation exercée par la Terre sur $P$

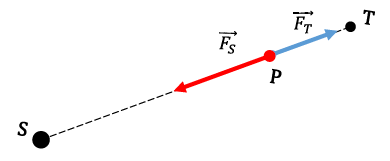
3.2.3.3. Relation entre $\dfrac{M_{T}}{M_{s}}\;,\ d\ $ et $\ \ell$

 

Théorème du centre d'inertie : $\vec{F}_{s}+\vec{F_{T}}=m\vec{a}$

 

$\begin{array}{lrcl}\Rightarrow&F_{s}-F_{T}&=&m.a_{n}\\ \\ \Rightarrow&\dfrac{G.M_{s}.m}{b^{2}}-\dfrac{G.M_{T}.m}{\ell^{2}}&=&m.a_{n}\\ \\ \Rightarrow&\dfrac{G.M_{s}.m}{b^{2}}-\dfrac{G.M_{T}.m}{\ell^{2}}&=&m.w^{2}b\\ \\ \Rightarrow&\dfrac{G.M_{s}}{b^{2}}-\dfrac{G.M_{T}}{\ell^{2}}&=&w^{2}b\quad\text{or }w^{2}=\dfrac{G.M_{s}}{d^{3}}\\ \\ \Rightarrow&\dfrac{G.M_{s}.m}{b^{2}}-\dfrac{G.M_{T}.m}{\ell^{2}}&=&\dfrac{G.M_{s}}{d^{3}}b\quad\text{or }b=(d-\ell)\\ \\ \Rightarrow&\dfrac{M_{s}}{(d-\ell)^{2}}-\dfrac{M_{s}}{d^{3}}(d-\ell)&=&\dfrac{M_{T}}{\ell^{2}}\\ \\ \Rightarrow&\ell^{2}\left(\dfrac{1}{(d-\ell)^{2}}-\dfrac{(d-\ell)}{d^{3}}\right)&=&\dfrac{M_{T}}{M_{s}}\end{array}$

 

3.2.3.4. Relation $\left(\dfrac{\ell}{d}\right)^{3}=\dfrac{M_{T}}{3.M_{s}}$

 

On a :

 

$\begin{array}{rcl} \ell^{2}\left(\dfrac{1}{(d-\ell)^{2}}-\dfrac{(d-\ell)}{d^{3}}\right)&=&\ell^{2}\left(\dfrac{d^{3}}{(d-\ell)^{2}d^{3}}-\dfrac{(d-\ell)^{3}}{(d-\ell)^{2}d^{3}}\right)\\ \\&=&\ell^{2}\left(\dfrac{d^{3}-(d-\ell)^{3}}{(d-\ell)^{2}d^{3}}\right)\\ \\ \Rightarrow\ \ell^{2}\left(\dfrac{d^{3}-d^{3}\left(1-\dfrac{\ell}{d}\right)^{3}}{\left(1-\dfrac{\ell}{d}\right)^{2}d^{5}}\right)&=&\dfrac{M_{T}}{M_{s}}\end{array}$

 

On pose $\dfrac{\ell}{d}=\varepsilon\ \Rightarrow\ 1-\dfrac{\ell}{d}=1-\varepsilon$

 

Dès lors : 

 

$\begin{array}{rcl}\ell^{2}\left(\dfrac{d^{3}-d^{3}\left(1-\dfrac{\ell}{d}\right)^{3}}{\left(1-\dfrac{\ell}{d}\right)^{2}d^{5}}\right)&=&\ell^{2}\left(\dfrac{d^{3}(1-\left(1-\varepsilon\right)^{3}}{\left(1-\varepsilon\right)^{2}d^{5}}\right)\\ \\&\approx&\ell^{2}\left(\dfrac{3\varepsilon}{d^{2}}\right)\end{array}$

 

si on fait l'approximation  $(1-\varepsilon)^{n}\approx 1-n\varepsilon$

 

Or $\varepsilon=\dfrac{\ell}{d}$

 

$\begin{array}{lrcl} \Rightarrow&\ell^{2}\left(\dfrac{3\varepsilon}{d^{2}}\right)&=&\dfrac{3\ell^{3}}{d^{3}}\\ \\ \Rightarrow&\dfrac{3\ell^{3}}{d^{3}}&=&\dfrac{M_{T}}{M_{s}}\\ \\ \Rightarrow&\left(\dfrac{\ell}{d}\right)^{3}&=&\dfrac{M_{T}}{3M_{s}}\end{array}$

 

d'où $\ell=d\times\sqrt[3]{\dfrac{M_{T}}{3M_{s}}}$

 

A.N : $\ell=1.5\;10^{6}\;km$

 

3.3. Un satellite tel que SOHO qui tourne d'un mouvement circulaire uniforme autour du Soleil permet d'observer le Soleil de façon continue. Un observatoire terrestre ne permet pas cela à cause de la rotation de la Terre sur elle-même au cours de son mouvement autour du Soleil.

 

3.4. Cette information n'est pas compatible avec le fait que SOHO effectue un mouvement circulaire uniforme autour du Soleil. En effet si l'attraction terrestre et celle du Soleil sur $P$ s'équilibraient on aurait $\sum \vec{F}_{\text{ext}}=\vec{0}$ et en conséquence $P$ devrait rester immobile dans le référentiel d'étude ou en mouvement rectiligne uniforme conformément au principe de l'inertie.

4.1. .

 

4.1.1.

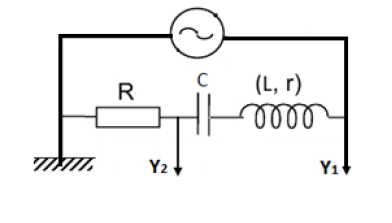
4.1.2. Les grandeurs $i(t)\ $ et $\ u_{R(t)}$ sont proportionnelles d'après la loi d'Ohm $(u_{R}=R.i)$ ; en conséquence les courbes qui les représentent ont la même allure.

 

4.2. .

 

4.2.1. Fréquence $N=\dfrac{1}{T}=\dfrac{1}{8.10^{-3}}=125\;Hz$

 

Tension maximale aux bornes du GBF : $U_{m}=1.8\times 5=9\;V.$

 

Intensité maximale : $I_{m}=\dfrac{U_{R\text{max}}}{R}=\dfrac{1\times 0.5}{50}=10\;mA$

 

4.2.2. Déphasage de la tension par rapport à l'intensité :

 

$u_{G}$ est en avance sur $i\;;\ \varphi_{u/i}=\dfrac{2\pi\times 1}{8}=\dfrac{\pi}{4}\;rad$

 

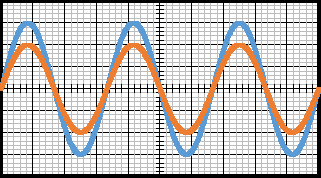
4.2.3. A la résonance d'intensité on aurait les deux tensions $u_{R(t)}\ $ et $\ u_{G(t)}$ en phase. L'allure des courbes 1 et 2 est schématisée ci-dessous.

4.3. .

 

4.3.1. A la résonance : $N_{0}=112.5\;Hz\ $ et $\ I_{0}=100\;mA.$

 

Inductance de la bobine :

 

$\begin{array}{lrcl}&LCw_{0}^{2}&=&1\\ \\ \Rightarrow&L&=&\dfrac{1}{4\pi^{2}N_{0}^{2}C}\\ \\& &=&\dfrac{1}{4\pi^{2}\times 112.5^{2}\times 5.10^{-6}}\\ \\& &=&0.4\;H\end{array}$

 

4.3.2. Bande passante : pour $I=\dfrac{I_{0}}{\sqrt{2}}$ on déduit graphiquement $\Delta N\approx 20\;Hz$

 

Facteur de qualité : $Q=\dfrac{N_{0}}{\Delta N}=\dfrac{112.5}{20}=5.6$

 

$Q$ renseigne sur l'acuité de la résonance. Plus $Q$ est grand plus la résonance est aigue, plus la bande passante est petite.

5.1. Le phénomène d'interférences lumineuses résulte de la superposition de radiations issues de sources lumineuses cohérentes ; il se traduit au niveau de l'écran par l'observation de franges brillantes qui alternent avec des franges sombres.

L'expérience des interférences lumineuses met en évidence le caractère ondulatoire de la lumière.

 

5.2.

Pour que le point $M$ d'abscisse $x$ soit sur une frange sombre, la différence de marche $\delta$ doit être un multiple impair de demi-longueur d'onde :

 

$\begin{array}{lrcl}&\delta&=&(2k+1)\dfrac{\lambda}{2}\\ \\& &=&\dfrac{a.x}{D}\\ \\ \Rightarrow&x&=&(2k+1)\dfrac{\lambda D}{2a}\\ \\& &=&\left(k+\dfrac{1}{2}\right)\dfrac{\lambda D}{a}\end{array}$

 

5.3. L'interfrange est la distance qui sépare les milieux de deux franges consécutives de même nature. $$x_{k+1}-x_{k}=\dfrac{\lambda D}{a}\ \Rightarrow\ i=\dfrac{\lambda D}{a}$$

 

5.4. .

 

5.4.1. Tableau :

 

$$\begin{array}{|l|c|c|c|c|}\hline a(10^{-3}\;m)&0.10&0.20&0.30&0.40\\ \hline i(10^{-3}\;m)&6.5&3.3&2.2&1.6\\ \hline a.i(10^{-6}\;m^{2})&0.65&0.66&0.66&0.64\\ \hline\end{array}$$

 

Le tableau montre que le produit 

 

$i.a=\text{cste}=C\approx 0.65\;10^{-6}\;m^{2}\ \Rightarrow\ i=C\dfrac{1}{a}.$

 

L'interfrange $i$ est donc inversement proportionnelle à la distance a entre les sources. Ce qui est en accord avec l'expression établie en 5.3. En effet on a :

 

$i=\dfrac{\lambda.D}{a}=\lambda.D\dfrac{1}{a}=\text{cste}\times\dfrac{1}{a}$

 

5.4.2. Longueur d'onde :

 

$\begin{array}{lrcl}&\lambda.D&=&i.a\ =\ 0.65\;10^{-6}\\ \\\Rightarrow&\lambda&=&\dfrac{0.65\;10^{-6}}{D}\\ \\ & &=&\dfrac{0.65\;10^{-6}}{1}\\ \\& &=&0.65\;10^{-6}\end{array}$

 

$\boxed{\lambda=650\;nm}$

 

$\begin{array}{lrcl}&W_{0}&=&\dfrac{hc}{\lambda_{0}}\\ \\\Rightarrow&\lambda_{0}&=&\dfrac{hc}{W_{0}}\\ \\ & &=&\dfrac{6.62\;10^{-34}\times 3\;10^{8}}{1.9\times 1.6\;10^{-19}}\\ \\\Rightarrow&\lambda_{0}&=&6.53\;10^{-7}\;m\end{array}$

 

$\boxed{\lambda_{0}=653\;nm}$

 

On a bien $\lambda<\lambda_{0}.$  Donc, il y a émission d'électrons par la cathode de la cellule : c'est l'effet photoélectrique.

 

L'effet photoélectrique met en évidence le caractère corpusculaire de la lumière.