Vous êtes ici

Corrigé Bac Physique Chimie 1er groupe S2-S2A-S4-S5 2014

Exercice 1

1.1. Équation-bilan de la réaction :

$HOOC-CH_{2}-CHOH-COOH\ \longrightarrow\ CH_{3}-CHOH-COOH$

1.2.

1.2.1. Schéma annoté du dispositif de dosage :

1.2.2. Équation-bilan de la réaction support du dosage du lait :

$CH_{3}-CHOH-COOH\ +\ (K^{+} + OH^{-})\ \longrightarrow\ CH_{3}-CHOH-COO^{-}\ +\ K^{+}+H_{2}O$

Déterminons la constante de réaction :

Si on note l'acide lactique

$AH\$ et

$\ A^{-}$ sa base conjuguée on a :

$\begin{array}{rcl} K&=&\dfrac{[A^{-}]}{[AH][OH^{-}]}\\ \\&=&\dfrac{[A^{-}][H_{3}O^{+}]}{[AH][OH^{-}][H_{3}O^{+}]}\\ \\&=&\dfrac{K_{a}(AH/A^{-})}{K_{a}(H_{2}O/OH^{-})}\\ \\&=&\dfrac{10^{-3.9}}{10^{-14}}\ =\ 10^{10.1}\ =\ 1.26\;10^{10}\end{array}$

$\boxed{K=1.26\;10^{10}>10^{3}}$ ; donc la réaction est totale.

1.2.3. Définition de l'équivalence acido-basique : il y a équivalence acido-basique lorsque les réactifs (acide et base) sont mélangés dans des proportions stœchiométriques.

Calcul de la concentration massique :

A l'équivalence on a :

$\begin{array}{rcrcl}\dfrac{n_{A}}{1}=\dfrac{n_{OH^{-}}}{1}&\Rightarrow&C_{A}.V_{A}&=&C_{b}.V_{bE}\quad\text{or }C_{A}=\dfrac{C_{m}}{M_{A}}\\ \\&\Rightarrow&\dfrac{C_{m}}{M_{A}}V_{A}&=&C_{b}.V_{bE}\\ \\&\Rightarrow&C_{m}&=&\dfrac{C_{b}.V_{bE}.M_{A}}{V_{A}} \end{array}$

A.N :

$C_{m}=\dfrac{0.1\times 8.4\times 90}{20}=3.8$

$\boxed{C_{m}=3.8\;g.L^{-1}>1.8\;g.L^{-1}}$ ; donc le lait dosé n'est pas frais.

1.2.4. Afin d'avoir un lait frais, il faut "stopper" la transformation du lactose en acide lactique par abaissement notoire de la température : on peut conserver le lait au réfrigérateur.

1.2.5. Diagramme de prédominance :

$pH$ du lait étudié étant supérieur au

$pk_{a}$ du couple, la forme basique (ion lactate) prédomine.

Exercice 2

2.1. Préparation du butanoate de méthyle

2.1.1. Le groupe fonctionnel présent dans le butanoate de méthyle :

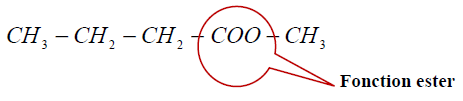
2.1.2. La famille du réactif

$B$ : alcool

2.1.3. Formules semi-développées et noms des réactifs

$A\$ et

$\ B$ :

Pour

$A\ :\ CH_{3}-CH_{2}-CH_{2}-COOH$ ; acide butanoïque

Pour

$B\ :\ HO-CH_{3}$ ; méthanol

2.1.4. Équation-bilan de la réaction entre

$A$ et

$B$ :

$CH_{3}-CH_{2}-CH_{2}-COOH + CH_{3}-OH\ \leftrightarrows\ CH_{3}-CH_{2}-CH_{2}-COO-CH_{3}\ +\ H_{2}O$

C'est la réaction d'estérification (directe) Caractéristiques de la réaction: elle est lente, limitée et athermique.

2.1.5. Calcul des quantités de matière minimales de

$A\$ et

$\ B$ :

$\begin{array}{lrcl}&r&=&\dfrac{n_{\text{ester}}^{\text{obtenu}}}{n_{\text{ester}}^{\text{théorique}}}.100\quad\text{or }n_{\text{ester}}^{\text{théorique}}=n_{A}^{\text{minimal}}=n_{B}^{\text{minimal}}\\ \\\Rightarrow&r&=&\dfrac{n_{\text{ester}}^{\text{obtenu}}}{n_{A}^{\text{minimal}}}.100\\ \\\Rightarrow&n_{A}^{\text{minimal}}&=&\dfrac{n_{\text{ester}}^{\text{obtenu}}}{r}.100\end{array}$

A.N :

$n_{A}^{\text{minimal}}=\dfrac{1}{67}100=1.49\;mol$

$\boxed{n_{A}^{\text{minimal}}=n_{B}^{\text{minimal}}=1.49\;mol}$

2.2. Étude cinétique de la réaction :

2.2.1. Si

$n_{A}=0.42\times 1=0.42\;mol$ ; l'abscisse obtenue à partir du graphe vaut :

$t_{1}\simeq 60\;min.$

2.2.2. Déduction de la quantité de matière de

$D$ formée :

$\begin{array}{lrcl}&n_{D}^{\text{formé}}&=&n_{A}^{\text{réagi}}\quad\text{or }n_{A}^{\text{réagi}}=n_{0A}-n_{A}^{\text{restant}}\\ \\ \Rightarrow&n_{D}^{\text{formé}}&=&n_{0A}-n_{A}^{\text{restant}}\end{array}$

A.N :

$n_{D}^{\text{formé}}=1-0.42=0.58\;mol$

$\boxed{n_{D}^{\text{formé}}=0.58\;mol}$

2.2.3. Calcul de la vitesse moyenne entre

$t=0\$ et

$\ t=t_{1}=60\;min$ :

$V_{m}=\dfrac{n_{A}(t_{0})-n_{A}(t_{1})}{t_{1}-t_{0}}$

A. N :

$V_{m}\thickapprox\dfrac{1-0.42}{60}=9.67\;10^{-3}\;mol.min^{-1}$

$\boxed{V_{m}=9.67\;10^{-3}\;mol.min^{-1}}$

2.2.4. Vitesse instantanée à

$t=45\;min$ :

La vitesse instantanée est donnée par la relation :

$V=-\dfrac{dn_{A}}{dt}$ graphiquement elle correspond à la valeur absolue du coefficient directeur de la tangente à la courbe au point d'abscisse

$t=45\;min$ (voir courbe ) :

On trouve :

$\boxed{V(t=45\;min)\simeq 5.11\;10^{-3}\;mol.min^{-1}}$

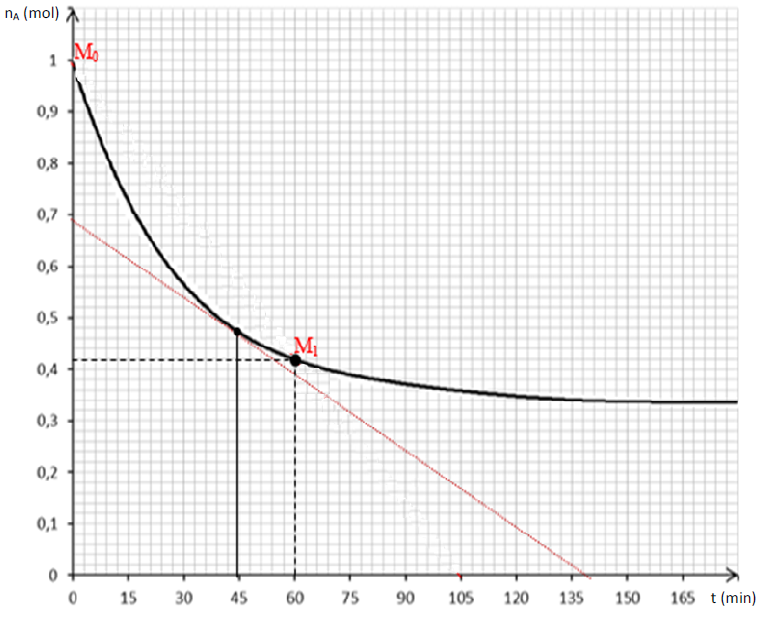
2.2.5. Détermination sans calcul de la vitesse moyenne entre

$t_{2}=165\;min\$ et

$\ t_{3}=180\;min$ :

A partir de la date

$t\simeq 150\;min$ , il n y a plus variation de la quantité de matière de

$A$ : la vitesse moyenne est nulle ; la réaction est terminée.

Exercice 3

3.1. Énoncer du théorème du centre d'inertie :

dans un référentiel galiléen, la somme des forces extérieures appliquées à un système de masse

$m$ est égale au produit de sa masse par le vecteur accélération

$\vec{a}_{G}$ de son centre d'inertie :

$\sum \vec{F}\;\text{(extérieures)}=m.\vec{a}_{G}$

3.2. Caractéristiques du vecteur-accélération :

On considère le projectile comme système et on rapporte le mouvement au référentiel terrestre supposé galiléen. L'action de l'air étant négligée, le projectile n'est soumis qu'à son poids.

$\begin{array}{rclcl}\text{T.C.I}\quad\sum \vec{F}\;\text{(extérieures)}=m.\vec{a}_{G}&\Rightarrow&\vec{P}&=&m.\vec{a}\\&\Rightarrow&m.\vec{g}&=&m.\vec{a}\\&\Rightarrow&\vec{a}&=&\vec{g} \end{array}$

$\vec{a}\;\left\lbrace\begin{array}{l}\text{direction : verticale}\\ \text{sens : orienté vers lebas}\\ \text{norme : }a=g=10\;m.s^{-2} \end{array}\right.$

3.3. Montrons que le mouvement est plan :

$\begin{array}{rcl}\vec{a}\;\left\lbrace\begin{array}{rcl} a_{x}&=&0\\ a_{y}&=&-g\\ a_{z}&=&0\end{array}\right.&\Rightarrow&\vec{V}\;\left\lbrace\begin{array}{rcl} V_{x}&=&V_{0}\cos\alpha\\ V_{y}&=&-gt+V_{0}\sin\alpha\\ V_{z}&=&0\end{array}\right.\\ \\&\Rightarrow&\overrightarrow{OM}\;\left\lbrace\begin{array}{rcl} x&=&V_{0}\cos\alpha.t\\ y&=&-\dfrac{1}{2}gt^{2}+V_{0}\sin\alpha.t\\ z&=&0\end{array}\right. \end{array}$

$x$ et

$y$ varient au cours du temps alors que

$z=o$ quelque soit la date

$t$ : le mouvement du projectile est plan et s'effectue dans le plan

$(xOy).$

3.4. Équation cartésienne de la trajectoire :

$x=V_{0}\cos\alpha.t\ \Rightarrow\ t=\dfrac{x}{V_{0}\cos\alpha.t}\$ or,

$\ y=-\dfrac{1}{2}gt^{2}+V_{0}\sin\alpha.t$

en remplaçant

$t$ dans l'expression de

$y$ on obtient :

$y=-\dfrac{g}{2.V_{0}^{2}\cos^{2}\alpha}x^{2}+x\tan\alpha$

3.5. Ordonnée du projectile pour

$x_{0}=800\;m$ :

$\begin{array}{lrcl}&y_{0}&=&-\dfrac{g}{2.V_{0}^{2}\cos^{2}\alpha}x_{0}^{2}+x_{0}\tan\alpha\\ \\ \Rightarrow&y_{0}&=&-\dfrac{10}{2.100^{2}\cos^{2}30^{\circ}}800^{2}+800\tan 30^{\circ}\\ \\& &=&35.2\;m\end{array}$

$\boxed{y_{0}=35.2\;m}$

$y_{0}$ est supérieure à la hauteur

$H$ ; le projectile passe au-dessus de l'oiseau ; l'oiseau ne sera pas atteint par ce projectile.

3.6. .

3.6.1. Expression de la portée en fonction de

$V_{0}\;,\ g\$ et

$\ \alpha$ :

Soit

$P$ le point d'impact au sol :

$y_{P}=0$

$\begin{array}{rcrcl} y_{P}=0&\Rightarrow&-\dfrac{g}{2.V_{0}^{2}\cos^{2}\alpha}x_{P}^{2}+x_{P}\tan\alpha&=&0\\ \\&\Rightarrow&x_{P}&=&\dfrac{2.V_{0}^{2}\cos^{2}\alpha.\tan\alpha}{g}\\ \\&\Rightarrow&x_{P}&=&\dfrac{2.V_{0}^{2}\cos^{2}\alpha.\sin\alpha}{g.\cos\alpha}\\ \\& & &=&\dfrac{2.V_{0}^{2}\cos\alpha.\sin\alpha}{g}\\ \\& & &=&\dfrac{V_{0}^{2}\sin 2\alpha}{g}\end{array}$

$\boxed{x_{P}=\dfrac{V_{0}^{2}\sin 2\alpha}{g}}$

3.6.2. Calcul de la portée maximale :

$x_{P}=\dfrac{V_{0}^{2}\sin 2\alpha}{g}$ est maximale si

$\sin(2\alpha)=1$

$\Rightarrow\ x_{P_{\text{max}}}=\dfrac{V_{0}^{2}}{g}$

A.N :

$x_{P_{\text{max}}}=\dfrac{100^{2}}{10}=1000\;m$

$\boxed{D=x_{P_{\text{max}}}=1\;km}$

3.6.3. Rayon du champ de tir :

$r=1.1\;D=1.1\;km$

Exercice 4

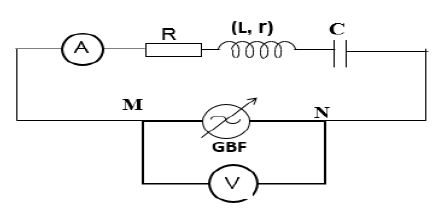
4.1. Schéma du circuit :

4.2. .

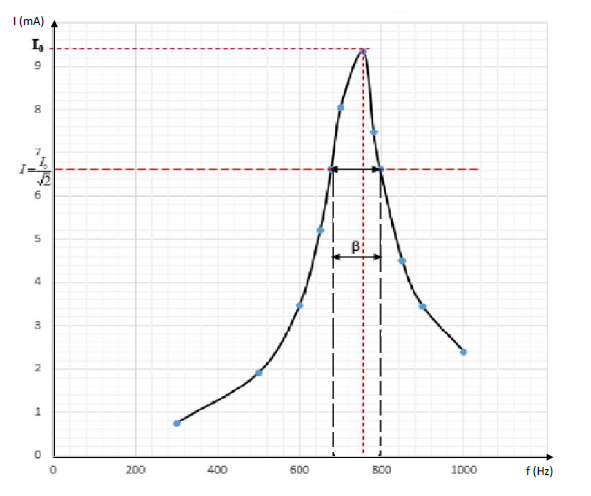
4.2.1. Le tracé de la courbe

$I=g(f)$

4.2.2. Graphiquement

$f_{0}$ est obtenue pour

$I$ maximale

$(I_{0}\thickapprox 9.35\;mA)\ :\ f_{0}\thickapprox 755\;Hz$

4.2.3. Calcul de l'impédance

$Z$ pour

$f=f_{0}$ : On est à la résonance d'intensité , donc

$Z=R_{\text{totale}}\$ et

$\ Z=\dfrac{U}{I_{0}}$

A.N :

$Z=\dfrac{1}{9.35\;10^{-3}}=107\;\Omega$

$\boxed{Z=107\;\Omega}$

Déduction de

$r$ :

$R_{\text{totale}}=r+R\ \Rightarrow\ r=R_{\text{totale}}-R$

A.N :

$r=107-80=27\;\Omega$

$\boxed{r=27\;\Omega}$

4.2.4. La largeur de la bande passante : c'est l'intervalle de fréquence pour lequel

$I=\dfrac{I_{0}}{\sqrt{2}}=\dfrac{9.35}{\sqrt{2}}=6.61\;mA$

Graphiquement on obtient

$\Delta f=\beta=120\;Hz$

4.2.5. Calcul de l'impédance aux extrémités de la bande passante :

$Z_{1}=\dfrac{U}{I_{1}}\$ et

$\ Z_{2}=\dfrac{U}{I_{_{2}}}\$ or

$\ I_{1}=I_{2}=\dfrac{I_{0}}{\sqrt{2}}=6.61\;mA$

$\Rightarrow\ Z_{1}=Z_{2}=\dfrac{1}{6.61\;10^{-3}}=151\;\Omega$

$\boxed{Z_{1}=Z_{2}=151\;\Omega}$

4.2.6. Calcul de

$L\$ et

$\ C$ :

$\beta=\dfrac{R+r}{2\pi.L}\ \Rightarrow\ L=\dfrac{R+r}{2\pi.\beta}$

A.N :

$L=\dfrac{107}{2\pi.120}=0.14\;H$

$\begin{array}{rcrcl} L.C.w_{0}^{2}=1&\Rightarrow&L.C.4\pi^{2}.f_{0}^{2}&=&1\\&\Rightarrow&C&=&\dfrac{1}{4\pi^{2}L.f_{0}^{2}}\end{array}$

A.N :

$C=\dfrac{1}{4\pi^{2}\times 0.142\times(755)^{2}}=3.13\;10^{-7}\;F$

$\boxed{L=0.14\;H\quad\text{et}\quad C=3.13\;10^{-7}\;F}$

Exercice 5

5.1. L'élément mercure, traceur isotopique :

5.1.1. La radioactivité

$\beta^{-}$ correspond à l'émission d'électrons par un noyau radioactif.

Équation de la réaction :

$_{80}^{203}Hg\ \longrightarrow\ _{-1}^{\;\ 0}e\ +\ _{Z}^{A}Y$

Les lois de conservations donnent :

$203=A\$ et

$\ 80=-1+Z$ ;

d'où,

$Z=81$ donc,

$_{Z}^{A}Y$ correspond au

$_{81}^{203}Tl$ d'où, l'équation

$_{80}^{203}Hg\ \longrightarrow\ _{-1}^{\;\ 0}e\ +\ _{81}^{203}Tl$

5.1.2. L'activité à

$t=0$ :

$\begin{array}{rcrcl} A_{0}=\lambda.N_{0}\quad\text{or } \lambda=\dfrac{\ln 2}{T}&\Rightarrow&A_{0}&=&\dfrac{N_{0}.\ln 2}{T}\\ \\& & &=&\dfrac{2.96\;10^{21}\times\ln 2}{46.69\times 24\times 3600}\\ \\& & &=&5.09\;10^{14}\;Bq \end{array}$

$\boxed{A_{0}=5.09\;10^{14}\;Bq}$

5.1.3. Durée au bout de laquelle l'activité diminue de

$0.14\;A_{0}$ :

A cette date

$\begin{array}{rcrcl} A=A_{0}-0.14.A_{0}=0.86.A_{0}&\Rightarrow&A_{0}.\mathrm{e}^{-\lambda t}&=&0.86.A_{0}\\&\Rightarrow&-\lambda t&=&\ln 0.86\\ \\&\Rightarrow&t&=&-\dfrac{\ln 0.86}{\lambda}=-T.\dfrac{\ln 0.86}{\ln 2}\\ \\&\Rightarrow&t&=&-46.69\times\dfrac{\ln 0.86}{\ln 2}\\ \\& & &=&10.16\;\text{jours} \end{array}$

$\boxed{t=10.16\;\text{jours}}$

5.2. Sécurisation des billets de banque par le mercure :

5.2.1. Le spectre d'émission ou d'absorption du mercure est discontinu.

5.2.2. Détermination de la transition responsable de cette fluorescence :

La lumière émise par la lampe à vapeur de sodium résulte d'une désexcitation des atomes de mercure. Cette lumière excite les nanos pigments qui émettent à leur tour par fluorescence.

$E_{\text{photon}}(\text{émis})=\Delta E=\dfrac{hC}{\lambda_{1}}$

A.N :

$E_{\text{photon}}(\text{émis})=\dfrac{6.62\;10^{-34}\times 3\;10^{8}}{253.6\;10^{-9}}=7.83\;10^{-19}\;J=4.89\;eV$

$\boxed{E_{\text{photon}}(\text{émis})=4.89\;eV}$

On vérifie que cette énergie correspond à :

$\Delta E=E_{2}-E_{0}$ : elle correspond donc à la transition du niveau

$E_{2}$ vers le niveau

$E_{0}$ pour le mercure.

5.2.3. Représentation de la transition :

5.2.4. La longueur d'onde maximale

$\lambda_{2}$ :

Lors d'une désexcitation d'un niveau

$p$ vers un niveau n la longueur d'onde de la radiation émise est donnée par :

$\lambda=\dfrac{hC}{E_{p}-E_{n}}$ ; comme cette désexcitation mène au niveau fondamentale donc

$E_{n}=E_{0}\ \Rightarrow\ \lambda=\dfrac{hC}{E_{p}-E_{0}}$

Pour que

$\lambda$ soit maximale il faut que

$E_{p}-E_{0}$ soit minimale donc

$E_{p}=E_{1}$

$\begin{array}{rcl}\Rightarrow\ \lambda_{\text{max}}=\lambda_{2}&=&\dfrac{hC}{E_{1}-E_{0}}\\ \\&=&\dfrac{6.62\;10^{-34}\times 3\;10^{8}}{(-5.77+10.44)\times 1.6\;10^{19}}\\ \\&=&2.66\;10^{-7}\;m \end{array}$

$\boxed{\lambda_{2}=266\;nm}$

5.2.5. Détermination de

$\lambda$ :

$\begin{array}{rcrcl} E_{2}-E_{1}=\dfrac{hC}{\lambda_{3}}&\Rightarrow&\lambda_{3}&=&\dfrac{hC}{E_{2}-E_{1}}\\ \\& & &=&\dfrac{6.62\;10^{-34}\times 3\;10^{8}}{(-5.55+5.77)\times 1.6\;10^{19}}\\ \\& & &=&5.64\;10^{-6}\;m \end{array}$

$\boxed{\lambda_{3}=5.64\;10^{-6}\;m}$

Relation entre

$\lambda_{1}\;,\ \lambda_{2}\$ et

$\ \lambda_{3}$ :

On a :

$\begin{array}{rcrcl} E_{2}-E_{0}=(E_{2}-E_{1})+(E_{1}-E_{0})&\Rightarrow&\dfrac{hC}{\lambda_{1}}&=&\dfrac{hC}{\lambda_{3}}+\dfrac{hC}{\lambda_{2}}\\ \\&\Rightarrow&\dfrac{1}{\lambda_{1}}&=&\dfrac{1}{\lambda_{3}}+\dfrac{1}{\lambda_{2}}\end{array}$

Ajouter un commentaire

form.antibot { display: none !important; } You must have JavaScript enabled to use this form.

Vous êtes ici

Corrigé Bac Physique Chimie 1er groupe S2-S2A-S4-S5 2014

Formulaire de recherche

Exercice 1

Exercice 2

Exercice 3

Exercice 4

Exercice 5

Ajouter un commentaire

Plain text