L'acide lactique, de formule $CH_{3}\;-\;CHOH\;-\;COOH$ est souvent désigné comme le principal responsable des crampes musculaires des sportifs lors de leurs sprints. On le retrouve dans le lait, le vin....

 

Dans le lait, les bactéries présentes provoquent, au cours du temps, la transformation d'une partie du lactose en acide lactique.

 

Dans le vin l'acide lactique se forme lors de la fermentation malolactique au cours de laquelle s'opère la décarboxylation de l'acide malique $HOOC\;-\;CH_{2}\;-\;CHOH\;-\;COOH.$

 

1.1. Écrire l'équation-bilan de la réaction de formation d'acide lactique dans le vin. $\quad(0.5\;pt)$

 

1.2. La présence d'acide lactique dans un lait est un indice de l'état de fraîcheur de ce lait. Plus la concentration d'acide lactique est élevée, moins le lait est frais. Par convention, dans l'industrie agroalimentaire, l'acidité d'un lait s'exprime en degré Dornic $(^{\circ}D).$ Un lait bien conservé (lait frais) présente une acidité Dornic inférieure à $18^{\circ}D$, ce qui correspond à une concentration massique de $1.8\;g.L^{-1}$ d'acide lactique dans le lait.

 

Un laborantin du service d'hygiène se propose de déterminer l'état de fraîcheur d'un lait retrouvé sur le marché. Il dose $20.0\;mL$ du lait, additionnés de $100\;mL$ d'eau distillée, par une solution d'hydroxyde de potassium $(K^{+}+HO^{-})$ de concentration molaire volumique $C_{b}=0.10\;mol.L^{-1}$ en présence de phénolphtaléine.

 

Le virage de l'indicateur est obtenu après addition d'un volume $V_{bE}=8.4\;mL$ de base.

 

1.2.1 Faire le schéma annoté du dispositif de dosage. $\quad(0.5\;pt)$

 

1.2.2 Écrire l'équation-bilan de la réaction support de dosage du lait. Montrer, par un calcul, que cette réaction est totale. $\quad(0.5\;pt)$

 

1.2.3 Définir l'équivalence acido-basique puis en déduire la concentration massique $C_{m}$ en acide lactique du lait étudié. Conclure sur l'état de fraîcheur du lait dosé. $\quad(01.5\;pt)$

 

1.2.4 Étant donnée la transformation, au cours du temps, d'une partie du lactose en acide lactique, sur quel facteur cinétique peut-on agir et comment afin d'avoir un lait frais? $\quad(0.25\;pt)$

 

1.2.5 En fait le lait étudié a un $pH$ initial égal à 4.9

 

Dresser un diagramme de prédominance puis dire quelle est la forme acide ou basique du couple acide lactique / ion lactate qui prédomine dans ce lait. $\quad(0.75\;pt)$

 

Données : 

 

$M(C)=12.0\;g.mol^{-1}\;;\ M(H)=1.0\;g.mol^{-1}\;;\ M(O)=16.0\;g.mol^{-1}.$

 

$pK_{a}\;\text{(acide lactique/ion lactate)}=3.9$

 

$K_{a}\;(H_{2}O / OH^{-})=10^{-14}\;;\ K_{a}\;(H_{3}O^{+} / H_{2}O)=1$

Le butanoate de méthyle, $CH_{3}\;-\;CH_{2}\;-\;CH_{2}\;-\;COO\;-\;CH_{3}$, est utilisé comme arôme dans l'industrie alimentaire et dans la parfumerie pour son odeur de pomme.

 

On se propose d'étudier une réaction de préparation du butanoate de méthyle et la cinétique de cette réaction.

 

2.1. Préparation du butanoate de méthyle.

 

2.1.1. Recopier la formule, entourer puis nommer le groupe fonctionnel présent dans la molécule du butanoate de méthyle. $\quad(0.25\;pt)$

 

2.1.2. Le butanoate de méthyle est obtenu en faisant réagir deux composés organiques $A\ $ et $\ B.$ 

 

Le réactif $A$ est un acide carboxylique. Préciser la famille du réactif $B.\quad(0.25\;pt)$

 

2.1.3. Écrire les formules semi-développées puis donner les noms des réactifs $A\ $ et $\ B.\quad(0.5\;pt)$

 

2.1.4. Écrire l'équation-bilan de la réaction entre les composés $A\ $ et $\ B.$

 

Donner le nom de cette réaction ; préciser ses caractéristiques. $\quad(0.75\;pt)$

 

2.1.5. Calculer les quantités de matière minimales de $A\ $ et $\ B$ à utiliser pour obtenir $1\;mol$ de butanoate de méthyle à partir d'un mélange équimolaire, le rendement de la réaction étant égal à $67\%.\quad(0.25\;pt)$

 

2.2. Étude cinétique de la réaction chimique.

 

Dans cette partie, l'équation-bilan de la réaction chimique est écrite sous la forme :

$$A+B\ \leftrightarrows\ D+H_{2}O$$ où $D$ est le butanoate de méthyle.

A la date $t_{0}=0$, on réalise un mélange équimolaire des réactifs $A\ $ et $\ B$ : 

$$n_{oA}=n_{oB}=1\;mol$$

 

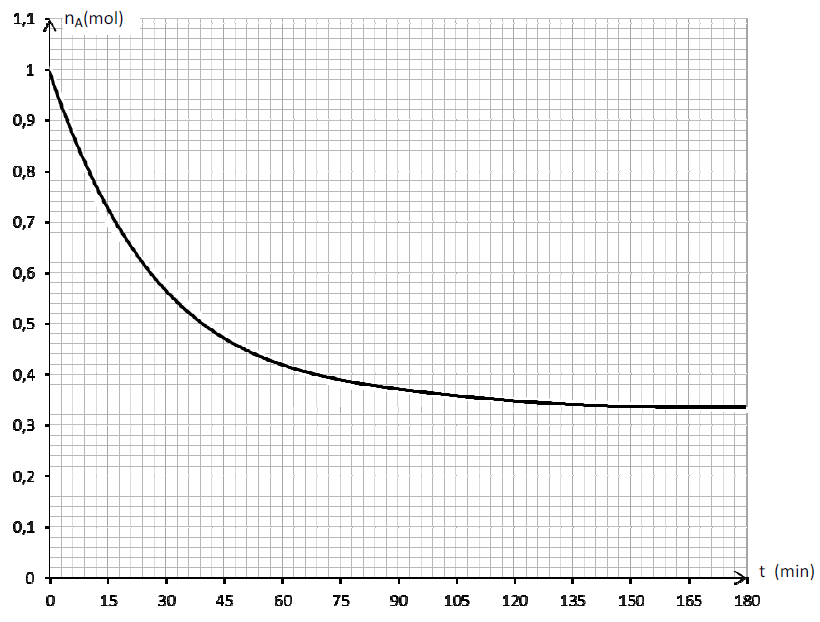
Des mesures ont permis de déterminer les quantités de matière d'acide carboxylique présent dans le mélange réactionnel au cours de la synthèse et de tracer la courbe $n_{A}=f(t)$ (voir courbe ci-dessous).

 

Par exploitation de cette courbe :

 

2.2.1. Retrouver la date t1 à laquelle la quantité d'acide carboxylique $(n_{A})$ présent dans le milieu, représente $42\%$ de la quantité initiale $(n_{oA})$ de $A.\quad(0.25\;pt)$

 

2.2.2. Déduire, à cette date t1, la quantité de matière de butanoate de méthyle formé.$\quad(0.5\;pt)$

 

2.2.3. Calculer la vitesse moyenne de disparition de l'acide carboxylique entre le début de la réaction et la date $t_{1}.\quad(0.5\;pt)$

 

2.2.4. Déterminer la vitesse instantanée de disparition de l'acide carboxylique à la date $t=45\;min.\quad(0.5\;pt)$

 

2.2.5. Déterminer, sans faire de calcul, la vitesse moyenne de disparition de l'acide carboxylique $A$ entre les dates $t_{2}=165\;min\ $ et $\ t_{3}=180\;min.$ Interpréter cette valeur.$\quad(0.25\;pt)$

 

NB : il n'est pas demandé de rendre la courbe avec la feuille de copie; toutefois on expliquera succinctement l'exploitation faite de cette courbe pour répondre aux questions.

La balistique est une science qui étudie le mouvement des projectiles. Les applications sont très nombreuses dans des domaines aussi variés que le sport, la balistique judiciaire ou les activités militaires.

 

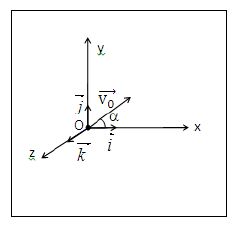
On étudie le mouvement d'un projectile ponctuel de masse $m$, lancé par un canon dans le champ de pesanteur uniforme $\vec{g}$ d'intensité $g=10\;m.s^{-2}.$

A un instant $t_{0}=0$, le projectile sort du canon en un point $O$ avec une vitesse initiale $\vec{v}_{0}$ faisant un angle $\alpha$ avec l'horizontale.

 

On suppose, que l'action de l'air est négligeable. Le point $O$ est au niveau du sol.

L'espace est rapporté au repère orthonormé $(O\;,\ \vec{i}\;;\ \vec{j}\;;\ \vec{k}).$

3.1. Énoncer la deuxième loi de Newton ou théorème du centre d'inertie.$\quad(0.25\;pt)$

 

3.2. Déterminer la direction, le sens et la norme du vecteur-accélération du projectile.$\quad(0.75\;pt)$

 

3.3. Montrer que le mouvement du projectile est plan. $\quad(0.5\;pt)$

 

3.4. Établir l'équation cartésienne de sa trajectoire dans le repère $(O\;,\ \vec{i}\;;\ \vec{j}\;;\ \vec{k}).\quad(0.5\;pt)$

 

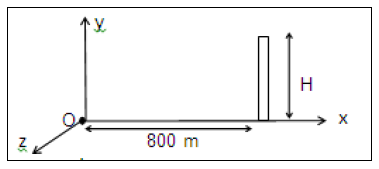
3.5 La vitesse de sortie du projectile, du canon, est de $100\;m.s^{-1}.$ La vitesse initiale fait l'angle $\alpha=30^{\circ}$ avec l'axe $Ox.$ Le projectile peut-il atteindre un oiseau perché au sommet d'un édifice se trouvant à $800\;m$ du point $O$, sur l'axe $Ox\ ?$ Justifier la réponse par le calcul. La hauteur de l'édifice est de $H=20\;m.\quad(01\;pt)$

 

3.6 Au cours d'un entrainement au tir, plusieurs essais sont effectués. Le projectile sort à chaque fois du canon en un point $O$ pris au sol avec une vitesse $\vec{v}_{0}$ de valeur $100\;m.s^{-1}$; mais l'angle de tir $\alpha$ varie. Pour protéger les personnes et les biens, on demande d'édifier une zone de sureté autour du point de lancement $O.$ Un mur de protection doit entourer la zone d'impact des projectiles. Le pourtour de ce mur est un "cercle" de centre $O$ et de rayon égal à $1.1\;D$ ; la distance $D$ étant la portée maximale du tir.

3.6.1 Établir l'expression de la portée du tir en fonction de $g\;,\ v_{0}\ $ et $\ \alpha.\quad(0.25\;pt)$

 

3.6.2 En déduire la valeur de la portée maximale. $\quad(0.25\;pt)$

 

3.6.3 Calculer le rayon du champ de tir. $\quad(0.5\;pt)$

Lors d'une séance de travaux pratiques, des élèves d'un lycée se proposent de déterminer la capacité d'un condensateur, l'inductance et la résistance d'une bobine trouvés dans le laboratoire, sans aucune étiquette.

 

Pour cela, ces élèves disposent du matériel suivant :

 

$-\ $ un générateur de basses fréquences (GBF), un conducteur ohmique de résistance $R=80\;\Omega$

 

$-\ $ la bobine d'inductance $L$ et de résistance $r$, le condensateur de capacité $C$

 

$-\ $ un ampèremètre de résistance négligeable, un voltmètre et des fils de connexion en quantité suffisante.

 

Les élèves réalisent un montage en série avec la bobine, le conducteur ohmique, le condensateur, l'ampèremètre et le générateur basse fréquence (GBF) qui délivre une tension sinusoïdale. Le voltmètre, branché aux bornes $M$ et $N$ du GBF, permet de vérifier que la tension efficace à ses bornes est maintenue constante et égale à $U=1.00\;V.$

 

4.1. Représenter le schéma du circuit électrique réalisé par les élèves. $\quad(0.5\;pt)$

 

4.2. Les élèves font varier la fréquence $f$ de la tension délivrée par le GBF, relèvent l'intensité efficace $I$ correspondante et obtiennent le tableau suivant :

$$\begin{array}{|c|c|c|c|c|c|c|c|c|c|c|c|c|}\hline f\;(Hz)&300&500&600&650&677&700&755&780&796&850&900&1000\\ \hline I\;(mA)&0.74&1.90&3.47&5.20&6.61&8.05&9.35&7.48&6.61&4.50&3.44&2.40\\ \hline\end{array}$$

 

4.2.1 Tracer la courbe de l'intensité efficace $I$ en fonction de la fréquence $f\ :\ I=g(f).\quad(0.5\;pt)$

 

Échelles : en abscisses : $15\;mm\ \rightarrow\ 100\;Hz$; en ordonnées : $20\;mm\ \rightarrow\ 1\;mA$

 

4.2.2. Déterminer graphiquement la fréquence $f_{0}$ de résonance du circuit. $\quad(0.25\;pt)$

 

4.2.3. Calculer l'impédance $Z$ du circuit pour $f=f_{o}.$ En déduire la résistance $r$ de la bobine $\quad(01\;pt)$

 

4.2.4. Déterminer la largeur de la bande passante $\beta$ du circuit. $\quad(0.5\;pt)$

 

4.2.5 Calculer l'impédance du circuit aux extrémités de la bande passante. $\quad(0.25\;pt)$

 

4.3. Ces élèves admettent que la largeur $\beta$ de la bande passante est telle que : $\beta=\dfrac{1}{2\pi}.\dfrac{R_{T}}{L}$ relation où $R_{T}$ désigne la résistance totale du circuit oscillant. Déterminer la valeur de l'inductance $L$ de la bobine et celle de la capacité $C$ du condensateur. $\quad(01\;pt)$

5.1. L'élément mercure, traceur isotopique :

 

Un "élément traceur" est un "élément" qui, par sa radioactivité, permet de suivre le sort d'une substance, son évolution au cours d'un processus physique, chimique ou biologique.

 

On se propose d'étudier la radioactivité de l'isotope mercure 203 $(_{80}^{203}Hg)$ qui est un traceur isotopique.

 

Cet isotope est radioactif $\beta^{-}$ ; sa période radioactive est $T=46.69\;\text{jours}.$

 

5.1.1. Rappeler la signification du terme "radioactivité $\beta^{-}$" et écrire l'équation de la réaction de désintégration du mercure 203. On identifiera le noyau fils à partir de l'extrait de tableau de classification périodique joint, en fin d'énoncé. $\quad(0.75\;pt)$

 

5.1.2 Initialement le nombre de noyaux radioactifs présents est : $N_{0}=2.96\;10^{21}\;\text{noyaux}.$

 

Déterminer l'activité $A_{0}$ de la source radioactive à la date $t_{0}=0.\quad(0.5\;pt)$

 

5.1.3 Déterminer la durée au bout de laquelle l'activité de la source radioactive diminue de $0.14\;A_{0}.\quad(0.75\;pt)$

 

5.2. Sécurisation des billets de banque par le mercure :

 

Les billets de banque authentiques peuvent être imprégnés de "nano pigments" pour être sécurisés.

 

Cela permet aux caissiers munis d'une lampe à vapeur de mercure en miniature de détecter les faux billets.

 

Lorsqu'un billet de banque sécurisé est éclairé par une lampe à vapeur de mercure, les "nano pigments", par fluorescence, se colorent en rouge ou en vert.

La radiation ultraviolette de longueur d'onde $\lambda_{1}=253.6\;nm$ permet d'observer une des couleurs obtenues par fluorescence.

 

Le diagramme ci-après représente, sans souci d'échelle, certains niveaux d'énergie de l'atome de mercure.

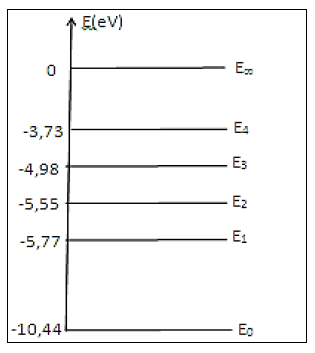
5.2.1 Le spectre d'émission ou d'absorption de l'atome de mercure est-il continu ou discontinu ? $\quad(0.25\;pt)$

 

5.2.2. Déterminer la transition énergétique responsable de la fluorescence des "nano pigments". $\quad(0.5\;pt)$

 

5.2.3. Reproduire le diagramme sur votre copie puis représenter là-dessus la transition associée par une flèche. $\quad(0.25\;pt)$

 

5.2.4. Déterminer la longueur d'onde maximale $\lambda_{2}$ de la radiation que peut émettre l'atome de mercure en passant de l'état excité à l'état fondamental. $\quad(0.25\;pt)$

 

5.2.5. Déterminer la longueur d'onde $\lambda_{3}$ de la radiation émise au cours de la transition $E_{2}\ \rightarrow\ E_{1}$ et établir la relation entre les longueurs d'onde $\lambda_{1}\;,\ \lambda_{2}\ $ et $\ \lambda_{3}\quad(0.75\;pt)$

 

Données : 

 

Constante de Planck : $h=6.62\;10^{-34}\;J.s$

 

Célérité de la lumière : $C=3.00\;10^{8}\;m.s^{-1}$

 

1 électron volt : $1\;eV=1.60\;10^{-19}\;J$

 

Extrait du tableau de classification périodique :

$$\begin{array}{|c|c|c|c|c|c|c|}\hline\text{Platine}&\text{Or}&\text{Mercure}&\text{Thalium}&\text{Plomb}&\text{Bismuth}&\text{Polonium}\\ \hline_{78}Pt&_{79}Au&_{80}Hg&_{81}Tl&_{82}Pb&_{83}Bi&_{84}Po\\ \hline \end{array}$$