Pour nous, les moustiques ne sont parfois qu'un désagrément. Mais leur prolifération peut avoir des conséquences dramatiques. Depuis fort longtemps, on utilise des molécules chimiques pour lutter contre les moustiques.

 

1.1 Le DEET est un liquide légèrement jaune à la température ambiante destiné à être appliqué sur la peau ou les vêtements. Il offre une protection contre les moustiques, puces et de nombreux autres insectes piqueurs. La formule semi-développée de sa molécule est représentée ci-contre.

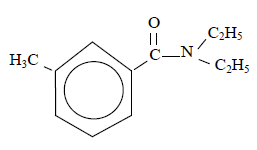
1.1.1 Recopier la formule. Entourer le(s) groupe(s) fonctionnel(s) présent(s) et le(s) nommer. $\quad(0.5\;pt)$

 

1.1.2 Le DEET peut être préparé en utilisant l'acide 3-méthylbenzoïque, le chlorure de thionyle et une amine.

 

a) Donner la formule, le nom et la classe de l'amine. $\quad(0.75\;pt)$

 

b) Écrire les équations-bilans des réactions correspondant à cette préparation. $\quad(0.5\;pt)$

 

1.1.3 Donner le nom du DEET en nomenclature officielle. $\quad(0.25\;pt)$

 

1.2 Le DEET est très efficace contre les moustiques et autres insectes piqueurs mais il est toxique à forte concentration.

Son utilisation à forte dose est déconseillée. Le produit IR3535 est utilisé aussi contre les moustiques ; il est légèrement moins efficace que le DEET mais moins nocif. Parmi les informations indiquées sur ce produit, on relève :

 

Nom : ester d'éthyle de l'acide 3-(N-acétyl-N-butyl) aminopropanoïque ; formule : $C_{11}H_{21}NO_{3}$

 

Écrire, à l'aide de ces données, la formule semi-développée de la molécule de IR3535. $\quad(0.5\;pt)$

Un laborantin se propose de suivre l'évolution de la réaction de saponification de l'éthanoate d'isopropyle avec la solution d'hydroxyde de sodium à température ambiante $(25^{\circ}\;C)$, réaction lente et totale. Pour cela, il prépare un mélange équimolaire de volume déterminé (volume supposé constant dans toute la suite).

 

2.1. Écrire l'équation-bilan de la réaction et nommer les produits obtenus. $\quad(0.5\;pt)$

 

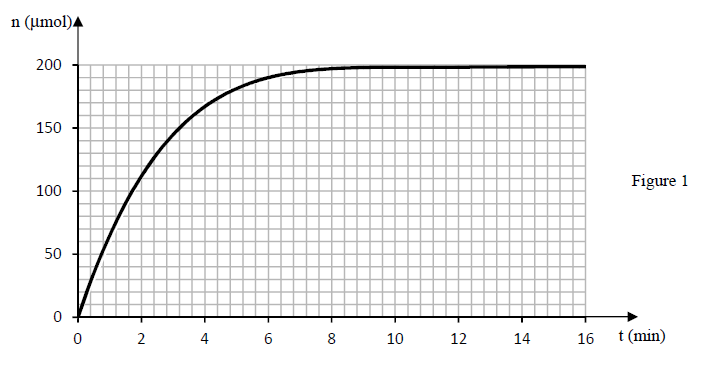
2.2.Dans une première expérience, le suivi de la réaction, par une méthode appropriée, a permis le tracé de la courbe d'évolution temporelle du nombre de moles d'éthanoate de sodium formé, noté $n$(en µmol) (figure 1).

 

2.2.1 Déterminer la vitesse de formation de l'éthanoate de sodium à la date $t=2\;min$ puis à $t=5\;min.$

Comment évolue la vitesse au cours du temps ? Justifier cette évolution. $\quad(0.5\;pt)$

 

2.2.2 Définir le temps de demi – réaction noté $t_{1/2}.\quad(0.25\;pt)$

 

2.2.3 Déterminer graphiquement:

 

a) la quantité de matière d'éthanoate de sodium obtenue en fin d'expérience;

 

b) le temps de demi-réaction $t_{1/2}.\quad(0.5\;pt)$

 

NB : Il n'est pas demandé de rendre la courbe ci-dessous avec la feuille de copie. Toutefois, on expliquera succinctement l'exploitation qui en est faite pour répondre aux questions précédentes.

2.3.Dans une seconde expérience, le laborantin a effectué des mesures lui permettant d'obtenir le tableau suivant :

 

$$\begin{array}{|c|c|c|c|c|c|c|c|c|c|} \hline\ln\left(\dfrac{C_{0}}{[OH^{-}]}\right)&0.0&0.8&1.6&2.4&3.2&4.0&4.8&5.6&6.4\\ \hline t\;(min)&0&2&4&6&8&10&12&14&16\\ \hline\end{array}$$

 

Dans ce tableau, la notation $\ln$ signifie logarithme népérien ; $C_{0}$ est la concentration des ions $OH^{-}$ dans le milieu à l'instant initial $t=0$ où les réactifs ont été mélangés et $[OH^{-}]$ est la concentration de ces ions à l'instant $t.$

 

2.3.1. a) Tracer la courbe représentative de $\ln\left(\dfrac{C_{0}}{[OH^{-}]}\right)=f(t)$ (à rendre avec la feuille de copie).

 

Échelles : 1 cm pour 1 min et 2 cm pour une unité de $\ln\left(\dfrac{C_{0}}{[OH^{-}]}\right)$

 

b) En déduire la relation entre $\ln\left(\dfrac{C_{0}}{[OH^{-}]}\right)\ $ et $\ t.\quad(01\;pt)$

 

2.3.2 Exprimer la concentration en ions hydroxyde $[OH^{-}]_{1/2}$ à la date $t_{1/2}$ en fonction de la concentration $C_{0}$ de ces ions dans le mélange à l'instant initial.

 

2.3.3 Montrer, en utilisant les résultats précédents, que le temps de demi-réaction $t_{1/2}$ a pour expression : $t_{1/2}=\dfrac{\ln 2}{k}$ , relation où $k$ est une constante dont on précisera la valeur. $\quad(0.5\;pt)$

 

2.3.4 En déduire une valeur de $t_{1/2}$ et comparer à la valeur trouvée à la question 2.2.3).

 

On prendra : $\ln 2=0.70\quad(0.25\;pt)$

Pour déterminer la charge massique d'une particule, on utilise un dispositif de déflexion électrique constitué de deux plaques conductrices $A\ $ et $\ B$ planes, horizontales, parallèles, de longueur $\ell$, distantes de $d$ (figure 2). 

Une particule de masse $m$ et de charge $q>0$ pénètre au point $O$ équidistant des deux plaques avec une vitesse $\vec{v}_{0}$ horizontale. Le dispositif est placé dans le vide et on ne tiendra pas compte du poids de la particule dans tout l'exercice.

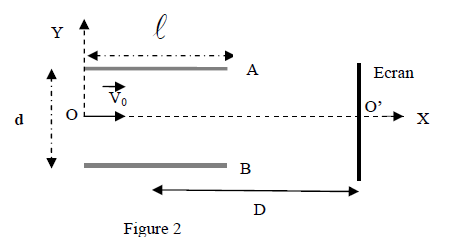
3.1. Exprimer, en fonction de $v_{0}$, $m$ et $q$, la tension $U_{0}$ sous laquelle la particule a été accélérée à partir d'une vitesse nulle pour atteindre cette vitesse $v_{0}.\quad(0.25\;pt)$

 

3.2. Un champ électrique uniforme $\vec{E}$ est créé par une tension constante $U_{AB}<0$ appliquée entre les plaques $A\ $ et $\ B.$

 

On pose $|U_{AB}|=U.$

 

3.2.1. Recopier la figure et représenter le vecteur champ électrique entre les plaques. $\quad(0.25\;pt)$

 

3.2.2. Le mouvement est rapporté au repère $(OX\;,\ OY).$ Établir l'équation de la trajectoire de la particule dans le champ électrique. Quelle est la nature de cette trajectoire ? $\quad(0.5\;pt)$

 

3.2.3. Exprimer l'ordonnée du point de sortie $S$ de la particule du champ électrique en fonction de $m\;,\ v_{0}\;,\ U\;,\ \ell\;,\ d\ $ et $\ q.\quad(0.25\;pt)$

 

3.2.4. Quelle condition doit remplir la tension $U$ pour que la particule puisse sortir du champ sans heurter les plaques ? $\quad(0.5\;pt)$

 

3.3. A sa sortie du champ électrique, la particule arrive en un point $P$ d'un écran placé perpendiculairement à l'axe $OX$, à la distance $D$ du milieu des plaques. Soit $O'$, le point d'intersection de l'axe $OX$ avec l'écran.

 

3.3.1. Quelle est la nature du mouvement de la particule à la sortie des plaques ? Justifier $\quad(0.25\;pt)$

 

3.3.2. Exprimer la déviation $Y= O'P$ de la particule en fonction de $m\;,\ q\;,\ U\;,\ d\;,\ \ell\;,\ D\ $ et $\ v_{0}.\quad(0.5\;pt)$

 

3.4. On établit, par un moyen approprié, un champ magnétique uniforme $\vec{B}$ perpendiculaire au champ électrique $\vec{E}$ dans l'espace compris entre les plaques. On règle la valeur de $\vec{B}$ de manière à ce que le spot initialement en $P$ soit ramené à $O'.$

 

3.4.1. Représenter alors le vecteur champ magnétique $\vec{B}.\quad(0.25\;pt)$

 

3.4.2. Exprimer l'intensité $B$ du vecteur champ magnétique en fonction de $v_{0}\;,\ U\;,\ d$ et calculer sa valeur $\quad(0.25\;pt)$

 

3.4.3. Établir l'expression de la charge massique $\dfrac{q}{m}$ de la particule en fonction de $Y\;,\ \ell\;,\ D\;,\ d\;,\ U\ $ et $\ B.\quad(0.5\;pt)$

 

3.4.4. Calculer le rapport $\dfrac{q}{m}$ et identifier la particule. $\quad(0.5\;pt)$

 

Données : 

 

$\ell=5\;cm\;;\ d=2\;cm\;;\ D=40\;cm\;;\ v_{0}=1.6\;10^{6}\;m.s^{-1}\;;\ U=400\;V\;;\ Y=O'P=1.5\;cm$

 

$$\begin{array}{|l|c|c|c|}\hline\text{Particule}&H^{+}&Li^{+}&He^{2+}\\ \hline\text{Charge massique }(10^{7}\;C.kg^{-1})&9.58&1.36&4.77\\ \hline \end{array}$$

Les interférences lumineuses permettent de déterminer de très petites distances, de l'ordre de $0.5\;\mu m.$

Elles trouvent leurs applications dans des domaines aussi variés que la métrologie, l'holographie, la détermination de l'indice de réfraction d'un gaz....

 

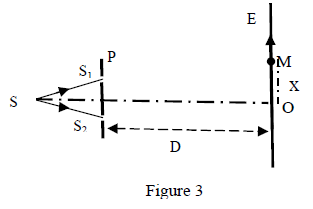
On réalise une expérience d'interférences lumineuses avec un dispositif des fentes de Young. Un faisceau de lumière issu d'une source ponctuelle $S$ est envoyé sur une plaque opaque P percée de deux fentes très fines $S_{1}\ $ et $\ S_{2}.$ La source $S$ est située sur l'axe de symétrie de $S_{1}S_{2}.$

 

La distance entre les deux fentes, notée a, est très faible. Un écran $E$ est placé orthogonalement au plan médiateur de $S_{1}S_{2}$ et à une distance $D$ de $S_{1}S_{2}.$ On désigne par $O$ la projection du milieu de $S_{1}S_{2}$ sur l'écran (figure 3).

Étude théorique

 

4.1 Recopier la figure, représenter les faisceaux diffractés par les sources $S_{1}\ $ et $\ S_{2}$ et indiquer la partie où l'on observe des interférences (zone d'interférences). $\quad(0.5\;pt)$

 

4.2 La source $S$ émettant une lumière monochromatique de longueur d'onde $\lambda$ et de pulsation $\omega$, les fentes $S_{1}\ $ et $\ S_{2}$ émettent des vibrations de la forme $Y_{01}=Y_{02}=S_{0}\sin\omega t.$ Les vibrations issues de $S_{1}\ $ et $\ S_{2}$ se superposent en tout point de la partie commune aux faisceaux diffractés.

 

On se propose de caractériser l'intensité lumineuse ou éclairement en tout point $M$ de l'écran repéré par son abscisse $x=OM.$ On désigne par $d_{1}\ $ et $\ d_{2}$ respectivement la distance entre le point $M$ et les sources $S_{1}\ $ et $\ S_{2}.$

 

La différence de marche est : $d=d_{2}-d_{1}\cong\dfrac{ax}{D}.$

 

4.2.1 Donner les expressions des vibrations issues de $S_{1}\ $ et $\ S_{2}$ au point $M$ en fonction de $\omega\;,\ t\;,\ d_{1}\;,\ d_{2}\ $ et $\ c$ célérité de la lumière. $\quad(0.5\;pt)$

 

4.2.2 On montre que la vibration résultante au point $M$ est donnée par l'expression : $$Y=2S_{0}\cos\left(\dfrac{\pi\delta}{\lambda}\right)\sin\omega\left(t-\dfrac{d_{1}+d_{2}}{2c}\right)$$

 

Que représente le coefficient $2S_{0}\cos\left(\dfrac{\pi\delta}{\lambda}\right)$ pour la vibration $Y\ ?\quad(0.5\;pt)$

 

4.2.3 L'intensité lumineuse ou éclairement $E$ au point $M$ est définie comme étant une grandeur proportionnelle à la puissance apportée par le rayonnement, cette puissance est elle-même proportionnelle au carré de l'amplitude $A$ de la vibration résultante en $M$, soit $E=CA^{2},$ relation où $C$ est une constante de proportionnalité.

 

a) Montrer que l'intensité lumineuse $E$ en $M$ peut se mettre sous la forme : $$E(x)=E_{0}\left(1+\cos\dfrac{2\pi x}{i}\right)$$

relation où on précisera l'expression de $E_{0}$ et celle de $i\quad(01\;pt)$

 

b) Calculer $E$, en fonction de $E_{0}$,pour les valeurs suivantes de $x$ : $$-i\;;\ -3\dfrac{i}{4}\;;\ -\dfrac{i}{2}\;;\ -\dfrac{i}{4}\;;\ 0\;;\ \dfrac{i}{4}\;;\ \dfrac{i}{2}3\dfrac{i}{4}\;;\ i$$

 

A l'aide des valeurs obtenues ébaucher le graphe $E(x)=f(x).\quad(01\;pt)$

 

c) A l'aide du graphe, préciser :

 

$-\ $ les abscisses des points où l'éclairement est maximal (franges brillantes) et celles des points où l'éclairement est nul(franges obscures) ; $\quad(0.5\;pt)$

 

$-\ $ la distance, en fonction de $i$, qui sépare les milieux de deux franges consécutives de même nature. $\quad(0.5\;pt)$

 

Application à la détermination de longueurs d'onde

 

4.3 L'exploration du champ d'interférences permet de déterminer la longueur d'onde d'une lumière monochromatique par mesure directe ou par comparaison de la figure d'interférences qu'elle produit avec celle d'une radiation de longueur d'onde connue. Dans la suite, on prendra : $D=2\;m\ $ et $\ a=1\;mm.$

 

4.3.1 La source $S$ émet une onde lumineuse bleue de longueur d'onde $\lambda_{1}$. A l'aide d'un instrument approprié, on mesure la distance correspondant à un ensemble de 10 interfranges sur l'écran ; cela donne $96\;mm.$ En déduire la valeur de $\lambda_{1}.$ Pourquoi mesurer la distance correspondant à 10 interfranges au lieu de celle qui correspond à 1 interfrange ? $\quad(0.5\;pt)$

 

4.3.2 La source $S$ émet maintenant une onde lumineuse rouge-orangée de longueur d'onde $\lambda_{2}.$ On constate que le milieu de la seconde frange sombre de cette lumière occupe la place qu'occupait le milieu de la seconde frange brillante de la lumière de longueur d'onde $\lambda_{1}.$ La frange centrale est notée zéro (0).

Déduire de cette expérience la longueur d'onde $\lambda_{2}$ de la lumière rouge-orangée. $\quad(0.5\;pt)$

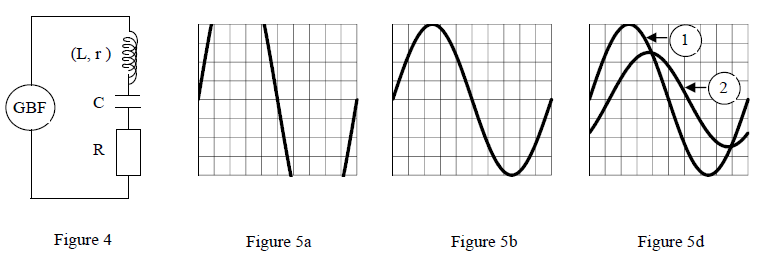
En travaux pratiques, des élèves se proposent de déterminer l'inductance $L$ et la résistance $r$ d'une bobine.

Pour cela, ils disposent du matériel suivant : la bobine en question, un générateur de tension sinusoïdale $G$ dont on peut faire varier la fréquence $f$ ; un conducteur ohmique de résistance $R=50\;\Omega$; un condensateur de capacité $C=8\;\mu F$; un oscilloscope bicourbe et des fils de connexion de résistance négligeable.

 

Chaque groupe d'élèves réalise un circuit série RLC (figure 4) et visualise, sur la voie $A$ de l'oscilloscope, la tension instantanée $u(t)$ aux bornes de l'ensemble RLC et sur la voie $B$, la tension instantanée $u_{R(t)}$ aux bornes du conducteur ohmique.

 

5.1 Reproduire la figure 4 sur la feuille de copie et faire figurer les branchements de l'oscilloscope. $\quad(0.5\;pt)$

 

5.2 En début de manipulation, un élève observe sur une voie la courbe représentée sur la figure 5a. Il modifie alors un réglage de l'oscilloscope et obtient la courbe représentée sur la figure 5b.

Préciser entre les réglages, base de temps (ou balayage horizontal) et sensibilité verticale de l'oscilloscope, lequel a été effectué par l'élève et dans quel sens (augmentation ou diminution) ? $\quad(0.5\;pt)$

 

5.3 Visualisant les tensions sur les 2 voies on obtient, sur l'écran de l'oscilloscope, les courbes de la figure 5d avec les réglages suivants : base de temps 1 ms/division ; sensibilité verticale pour les 2 voies 0.2 V / division.

 

5.3.1 Identifier les tensions représentées par les courbes (1) et (2). Justifier. $\quad(0.5\;pt)$

 

5.3.2 Expliquer pourquoi en visualisant la tension $u_{R(t)}$ sur la voie $B$, par la même occasion, on visualise l'intensité $i(t)$ dans le circuit. $\quad(0.5\;pt)$

 

5.4 A partir de la figure 5d, déterminer :

 

5.4.1 la fréquence des oscillations ; $\quad(0.5\;pt)$

 

5.4.2 la valeur maximale de $u(t)$ et la valeur maximale de $i(t).$ En déduire la valeur de l'impédance $Z$ du circuit ; $\quad(0.75\;pt)$

 

5.4.3 la différence de phase $\varphi$ de $u(t)$ par rapport à $i(t).$ On précisera si $u(t)$ est en avance ou en retard sur $i(t).$

 

En déduire la résistance $r$ et l'inductance $L$ de la bobine. $\quad(01.25\;pt)$