Bac Physique chimie 1er groupe S1 S3 2007

Le développement de la chimie organique de synthèse, à la fin du $XIX^{e}$ siècle, a conduit à des substances d'odeurs attrayantes qui ont eu une grande influence sur la parfumerie.

 

Les substances odorantes appartiennent à des familles très diverses de composés chimiques : alcools, aldéhydes, cétones ou esters.

 

Parmi ces derniers, on peut citer l'acétate de benzyle présent dans l'essence de jasmin et le salicylate de méthyle constituant principal de l'essence de Wintergreen extraite de certaines plantes.

 

1.1 Pour chaque famille de composés citée dans le texte écrire la formule du groupement fonctionnel puis donner un exemple de composé (formule semi-développée et nom) de la famille.  (01 point)

 

1.2 La formule semi-développée de l'acétate de benzyle est :

 

De quel acide et de quel alcool dérive l'acétate de benzyle ?

 

Écrire l'équation-bilan de la préparation de l'acétate de benzyle à partir de ces composés et préciser les caractéristiques de cette réaction.  (0.50 point)

 

1.3 Un laborantin prépare le salicylate de méthyle par réaction de l'acide salicylique (ou acide $2$-hydroxybenzoïque $HO-C_{6}H_{4}-COOH$) avec le méthanol.

 

Pour ce faire, il introduit dans un ballon une masse de $13.7\,g$ d'acide salicylique, un volume de $12\,mL$ de méthanol et quelques gouttes d'acide sulfurique concentré. 

 

Il procède au chauffage pendant une heure. 

 

La réaction terminée, le mélange est refroidi puis séparé. 

 

Après séchage de la phase organique, une masse de $11.4\,g$ de salicylate de méthyle est obtenue.

 

1.3.1 Écrire l'équation-bilan de la réaction.  (0.25 point)

 

1.3.2 Déterminer le réactif limitant ou réactif en défaut.  (0.50 point)

 

1.3.3 Quel est le rôle de l'acide sulfurique ? 

 

Et pourquoi chauffe t-on ?  (0.25 point)

 

1.3.4 Calculer le rendement de cette préparation.  (0.5 point)

 

Données : 

 

$M(\text{acide salicylique})=138\,g/mol$ ; 

 

$M(CH_{3}OH)=32\,g/mol$

 

$M(\text{salicylate de méthyle})=152\,g/mol$

 

Masse volumique du méthanol : $\rho=0.80\,kg\cdot L^{-1}.$

On étudie l'évolution dans le temps de la transformation, en solution aqueuse, des ions iodure $I^{-}$ en diiode $I_{2}$ par l'action d'un réactif approprié. 

 

La réaction peut être représentée par l'équation :

 

Cette réaction est lente mais totale.

 

Pour étudier la cinétique de la réaction on mélange les deux réactifs dans les proportions stoechiométriques à la date $t=0.$ 

 

Un dispositif approprié permet de déterminer, au fur et à mesure, la concentration molaire volumique du diiode et de modéliser la loi de variation de cette concentration en fonction du temps.

 

2.1 Montrer que cette transformation correspond à une réaction d'oxydoréduction et préciser les couples oxydant-réducteur mis en jeu.  (0.50 point)

 

2.2 Pendant les $210$ premières minutes, la concentration molaire volumique de diiode $[I_{2}]=C$ varie en fonction du temps suivant la loi :

 

$C=5\cdot 10^{-3}\left(1-\mathrm{e}^{-\dfrac{t}{2}}\right)$, avec $C$ en $mol\cdot L^{-1}$ et $t$ en heure.

 

2.2.1 Compléter le tableau suivant et tracer la courbe $C=f(t)$ dans l'intervalle considéré.  (01 point.)

$$\begin{array}{|c|c|c|c|c|c|c|c|c|} \hline t\,(min)&0&30&60&90&120&150&180&210\\ \hline C\,(mol\cdot L^{-1})& & & & & & & &\\ \hline \end{array}$$

 

2.2.2 Déterminer, à l'aide du graphe, la vitesse $v$ de formation du diiode à la date $t=100\,min.$   (0.50 point)

 

2.2.3 Établir l'expression de la vitesse $v$ de formation du diiode en fonction du temps dans l'intervalle $[0\;;\ 210\,min].$ 

 

Quelle valeur de $v$ à la date $t=100\,min$ obtient-on par le calcul ?  (0.50 point)

 

2.3 Montrer, à partir de l'expression précédente, que la vitesse de formation du diiode est une fonction décroissante du temps durant cette expérience.

 

Pourquoi en est-il ainsi ?  (0.50 point)

On donne : 

 

Masse de la Terre : $M_{T}=5.97\cdot 10^{24}kg$ ; 

 

Rayon de la Terre : $R_{T}=6370\,km$ ;

 

Masse du satellite : $m=650\,kg$ ; 

 

Constante de gravitation : $G=6.67\cdot 10^{-11}N\cdot m^{2}\cdot kg^{-2}.$

 

SPOT est un satellite de télédétection. 

 

Il évolue à l'altitude $h=832\,km$ sur une trajectoire circulaire contenue dans un plan passant par l'axe des pôles de la Terre. 

 

Un tel satellite est appelé satellite à défilement.

 

3.1 Montrer que le mouvement du satellite est uniforme. 

 

Donner alors l'expression de sa vitesse $V$ en fonction de $G$, $M_{T}$, $R_{T}$ et $h.$ 

 

Faire l'application numérique.  (0.75 point)

 

3.2 Établir l'expression de la période de révolution du satellite SPOT en fonction de $G$, $M_{T}$, $R_{T}$ et $h.$  (0.25 point)

 

3.3 Calculer l'angle de rotation de la Terre pendant une révolution du satellite. 

 

Pourquoi dit-on qu'un tel satellite est un satellite à défilement ?  (0.50 point)

 

3.4 Dans le champ de gravitation terrestre l'énergie potentielle du satellite est donnée par :

$$E_{p}=-\dfrac{GM_{T}m}{r}\text{ avec }r=R_{T}+h.$$

 

3.4.1 Où a-t-on choisi la référence de l'énergie potentielle de gravitation ? 

 

Justifier la réponse.  (0.25 point)

 

3.4.2 Exprimer l'énergie mécanique du satellite en fonction de $G$, $M_{T}$, $m$, $R_{T}$ et $h$ puis en fonction de $m$ et $V$, vitesse du satellite.  (0.50 point)

 

3.4.3 Calculer l'énergie mécanique du satellite à l'altitude $h.$  (0.25 point)

 

3.5 Le satellite SPOT est équipé d'un moteur permettant de corriger sa trajectoire.

 

3.51 Montrer que si le moteur fonctionne, toute variation $\Delta\,E_{m}$ de l'énergie mécanique du satellite s'accompagne de variation simultanée $\Delta\,h$ de son altitude et $\Delta\,V$ de sa vitesse.  (0.50 point)

 

3.5.2 En utilisant les résultats des questions précédentes, exprimer la variation d'altitude $\Delta\,h$ et la variation de vitesse $\Delta\,V$ corrélatives à une variation d'énergie mécanique $\Delta\,E_{m}.$  (01 point)

 

Calculer ces variations pour $\Delta\,E_{m}=5\,MJ.$ 

 

On prendra $h=832\,km$ et on utilisera les valeurs numériques trouvées précédemment pour $V$ et $E_{m}.$  (0.50 point)

Les deux parties de l'exercice sont indépendantes.

 

Première partie

 

Dans cette partie on se propose de comparer le fonctionnement d'un oscillateur électrique avec celui d'un oscillateur mécanique pour faire ressortir des analogies.

 

4.1 On réalise un circuit comprenant une bobine d'inductance $L$ dont la résistance est supposée nulle et un condensateur de capacité $C$ ; initialement l'interrupteur $K$ est ouvert [figure (a)].

 

 

 

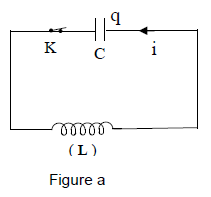
Le condensateur est d'abord chargé sous une tension constante $U$ par un dispositif non représenté sur la figure. 

 

On ferme ensuite l'interrupteur $K.$

 

4.1.1 Établir l'équation différentielle traduisant les oscillations électriques qui se déroulent dans le circuit en prenant comme variable la charge $q$ d'une armature du condensateur. 

 

[Le circuit est orienté comme indiqué sur la figure (a)].  (0.50 point)

 

4.1.2 En déduire la période des oscillations. 

 

Applications numériques : $L=0.10H$ ; $C=1.0\cdot 10^{-5}F.$  (0.50 point)

 

4.2 On considère un solide $A$ de masse $m$ pouvant glisser sans frottement sur un support horizontal.

 

Le solide est lié à l'une des extrémités d'un ressort de masse négligeable et de raideur $k$ ; l'autre extrémité du ressort étant fixée en un point $E$ (figure b).

 

 

 

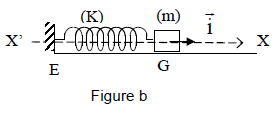
On déplace le solide $A$ de façon à provoquer l'allongement du ressort et on l'abandonne sans vitesse initiale.

 

4.2.1 Établir l'équation différentielle du mouvement du solide $A$ en prenant comme variable l'élongation $x$ du solide, le mouvement étant rapporté au repère $X'X$ dont l'origine coïncide avec la position du centre d'inertie $G$ du solide à l'équilibre [figure (b)]  (0.50 point)

 

4.2.2 En déduire la période des oscillations. 

 

Applications numériques : $m=0.50\,kg$ ; $k=25N/m.$  (0.50 point)

 

4.3 Recopier puis compléter le tableau ci-dessous pour faire apparaître les analogies entre les grandeurs électriques de la question 4.1 et les grandeurs mécaniques de la question 4.2  (01.5 point)

$$\begin{array}{|c|c|} \hline \text{Grandeurs mécaniques}&\text{Grandeurs électriques}\\ \hline \text{Masse }(m)& \\ \hline \text{Raideur du ressort }(k)&\\ \hline\text{Elongation }(x)&\\ \hline \text{Vitesse }(V)&\\ \hline \text{Energie cinétique }E_{c}\left(1/2kx^{2}\right)&\\ \hline \text{Energie potentielle élastique }E_{pe}\left(1/2kx^{2}\right)&\\ \hline \end{array}$$

 

Deuxième partie

 

Un générateur $BF$ maintenant entre ses bornes une tension sinusoïdale de fréquence $N$, alimente un circuit contenant en série une bobine d'inductance $L=36\,mH$ et de résistance $R_{1}$ et un résistor de résistance $R_{2}=12.5\Omega.$ 

 

 

 

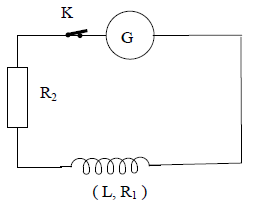
La tension efficace aux bornes du générateur est $U=64\,V.$

 

On mesure l'intensité efficace du courant, on trouve $I=3.2\,A.$

 

Puis l'on mesure la tension efficace $U_{1}$ aux bornes de la bobine et la tension efficace $U_{2}$ aux bornes du résistor, on trouve $U_{1}=U_{2}.$

 

4.4 Montrer que les impédances $Z_{1}$ de la bobine et $Z_{2}$ du résistor sont égales. 

 

Donner la valeur numérique commune.  (0.50 point)

 

4.5 Construire le diagramme de Fresnel relatif au circuit.

 

On posera : $i=I\sqrt{2}\sin(\omega\,t)$ et $u=U\sqrt{2}\sin(\omega\,t+\phi)$ respectivement pour l'intensité instantanée $i$ du courant et la tension instantanée $u$ aux bornes du générateur.  (0.50 point)

 

4.6 Calculer les valeurs numériques de $\phi$, de $R_{1}$ et du produit $L\omega.$ 

 

Calculer alors la valeur de la fréquence.  (01 point)

Données : 

 

Constante de Planck $h=6.62\cdot 10^{-34}J\cdot s$ ; 

 

célérité de la lumière dans le vide : $C=3\cdot 10^{8}m/s$

 

$E_{0}=13.6\,eV$ ; 

 

masse de l'électron : $m=9.1\cdot 10^{-31}kg.$

 

Un ion hydrogénoÏde est un ion ayant la même structure électronique que l'atome d'hydrogène ; c'est-à-dire possédant un seul électron gravitant autour du noyau. 

 

C'est le cas des ions hélium $He^{+}$ et lithium $Li^{2+}.$

 

Un électron unique gravitant autour d'un noyau de numéro atomique $Z$ sur le niveau $n$ possède l'énergie $E_{n}=-\dfrac{E_{0}Z^{2}}{n^{2}}$

 

5.1 L'électron passe d'un niveau d'énergie $E_{n}$ à un niveau inférieur d'énergie $E_{p}.$

 

5.1.1 Y a-t-il absorption ou émission de photon ? 

 

Justifier.  (0.25 point)

 

5.1.2 Exprimer la longueur d'onde de la radiation correspondante $\lambda_{(n\,\ p)}$ en fonction de $E_{0}$, $Z$, $n$, $p$, $h$ et $c.$  (0.50 point)

 

5.2 On peut écrire cette longueur d'onde $\lambda(n\;,\ p)$ sous la forme :

$$\lambda(n\;,\ p)=\dfrac{1}{R}\left(\dfrac{n^{2}p^{2}}{n^{2}-p^{2}}\right)$$

 

où $R$ est une constante appelée constante de Rydberg.

 

5.2.1 Exprimer $R$ en fonction de $E_{0}$, $Z$, $h$ et $C.$  (0.50 point)

 

5.2.2 Calculer cette constante dans les cas suivants :

 

$\bullet$ Atome d'hydrogène $H$ : $R=R_{1}$

 

$\bullet$ Ion $He^{+}$ : $R=R_{2}$

 

$\bullet$ Ion $Li^{2+}$ : $R=R_{3}$  (0.50 point)

 

5.3 On considère la série de Balmer dans le spectre atomique de l'hydrogène : 

 

Il s'agit de l'ensemble des raies correspondant à des transitions décroissantes qui ramènent l'atome d'hydrogène d'un niveau excité $n$ au niveau $p=2.$

 

Calculer l'écart $\Delta\lambda$ entre la plus grande et la plus courte des longueurs d'onde de cette série.  (0.50 point)

 

5.4 Calculer l'énergie d'ionisation de l'atome d'hydrogène $(Z=1)$ et des ions hydrogénoïdes $He^{+}(Z=2)$ et $Li^{2+}(Z=3).$  (0.75 point)

 

5.5. On envoie sur des atomes d'hydrogène pris à l'état fondamental des photons d'énergie respective $1.9\,eV$, $3.4\,eV$, $10.2\,eV$ et $14\,eV.$

 

5.5.1 Quel(s) est (sont) le les) photon(s) susceptible (s) d'être absorbé(s) ?

 

Justifier la réponse.  (0.50 point)

 

5.5.2 Montrer que si l'atome d'hydrogène pris à l'état fondamental absorbe un photon d'énergie $14\,eV$, il émet un électron. 

 

Calculer la vitesse d'éjection de l'électron.  (0.25 point)

 

Vérifier que cet électron n'est pas relativiste.  (0.25 point)

Une particule est dite relativiste si sa vitesse est supérieure au dixième de la célérité de la lumière dans le vide.