Vous êtes ici

Devoir n° 3 - Physique chimie - 2nd S

Classe:

Seconde

NB :

L'utilisation du tableau de classification périodique est formellement interdite.

Exercice 1

Compléter le tableau suivant :

$$\begin{array}{|c|c|c|c|c|c|} \hline \text{Symbole de l'atome}&\text{Symbole du}&\text{Charge}&\text{Nombre de}&\text{Nombre de}&\text{Nombre }\\ \hline \text{ou de l'ion}&\text{noyau}& &\text{protons}&\text{neutrons}&\text{d'électrons}\\ \hline B& & & &6&5\\ \hline & & &14&14&14\\ \hline Mg^{2+}&_{12}^{25}Mg& & & &\\ \hline &_{17}^{35}Cl&-e& & &\\ \hline & &+3e& &30&23\\ \hline \end{array}$$

Données :

$$\begin{array}{|c|c|c|c|} \hline \text{Numéro atomique }Z&24&25&26\\ \hline \text{Symbole}&Cr&Mn&Fe\\ \hline \end{array}$$

Exercice 2

2.1 Établir le schéma de Lewis des éléments suivants :

Hydrogène $(Z=1)$ ;

Carbone $(Z=6)$ ;

Azote $(Z=7)$ et Oxygène $(Z=8)$

2.2 Après avoir défini le terme « molécule », donner la formule développée des molécules suivantes :

a) $C_{2}H_{6}O$ ;

b) $CH_{2}N_{2}$ ;

c) $CH_{2}O.$

2.3 La formule brute de la molécule d'éthylamine est $C_{2}H_{7}N.$

Un élève propose la formule de Lewis suivante pour cette molécule :

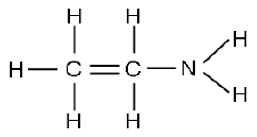
a) Montrer que cette représentation de Lewis est incorrecte.

b) Donner la formule de Lewis correcte de la molécule d'éthylamine.

On considère les ions suivants :

$$\begin{array}{|c|c|c|c|c|c|c|} \hline \text{ion}&\text{Sodium}&\text{Calcium}&\text{Plomb}&\text{Nitrate}&\text{Sulfate}&\text{Phosphate}\\ \hline \text{formule}&Na^{+}&Ca^{2+}&Pb^{2+}&NO_{3}^{-}&SO_{4}^{2-}&PO_{4}^{3-}\\ \hline \end{array}$$

Donner les formules ioniques, puis les formules statistiques des composés dont les noms suivent : phosphate de calcium ; nitrate de plomb et sulfate de sodium.

2.4 On considère le composé ionique de formule statistique $Al_{2}(SO_{4})_{3}.$

Donner son nom et sa formule ionique.

Exercice 3 (04 points)

Un mobile $M$ décrit un mouvement circulaire uniforme sur une trajectoire de diamètre $d=30\,cm$ à la vitesse angulaire $\omega$ dans le sens positif trigonnométrique.

A $t_{0}=0\,s$ le mobile $M$ occupe la position d'abscisse angulaire $\theta_{0}.$

L'équation horaire de son abscisse angulaire est donnée par l'expression :

$$\theta(t)=2\pi\cdot t+\dfrac{\pi}{4}$$

3.1 Définir les termes suivants : mouvement circulaire uniforme $(MCU)$ ; période $T$ d'un mouvement circulaire. (01 pt)

3.2 Déduire de l'équation horaire, la vitesse angulaire $\omega$ du mobile $M$ et l'abscisse angulaire à l'instant initial.

Calculer la période $T$ du mouvement.

3.3 Représenter la trajectoire de ce mobile à l'échelle $\dfrac{1}{5}$ $(1\,cm\ \rightarrow\ 5\,cm).$

Placer le point $M_{0}$ occupé par le mobile à l'instant $t_{0}.$

3.4 Calculer la valeur du vecteur vitesse $\overrightarrow{V}$ de ce mobile.

Représenter à l'instant $t_{0}$ à l'échelle $1\,cm\ \rightarrow\ 5\cdot10^{-1}m/s.$

Exercice 4

4.1 Une boule de pétanque de diamètre $73\,mm$, a une masse de $700\,g.$

L'acier qui la compose a une masse volumique de $7.8\,g/cm^{3}.$

Cette boule est-elle pleine ou creuse ?

Justifier.

4.2 En travaux pratique, un groupe d'élève désire déterminer la densité de la pierre et celle de l'alcool.

Ils font des mesures schématisées ci-dessous :

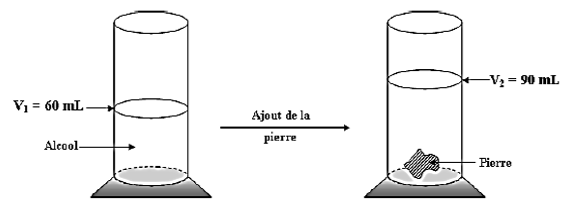
a) Calculer le volume $V_{P}$ de la pierre.

En déduire sa masse volumique $\rho_{P}$ ainsi que sa densité sachant sa masse est $m_{P}=87\,g.$ (01.5 pt)

b) Le contenu de deuxième éprouvette possède une masse volumique de $\rho=1.5\,g/cm^{3}.$

$-\ $ Déterminer la masse $m_{A}$ de l'alcool contenu dans cette éprouvette. (0.75 pt)

$-\ $ En déduire la déduire la densité $d_{A}$ de l'alcool. (0.75 pt)

On rappelle : une sphère de rayon $r$, a pour volume ; $V=\dfrac{4}{3}\pi\,r^{3}$ ; $\rho_{air}=1.29g/L$ et $\rho_{eau}=1000g/L.$

Exercice 5

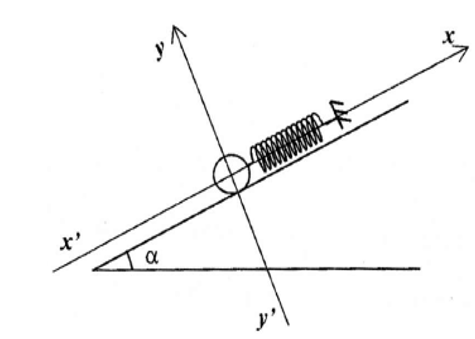
Un solide $(S)$ de masse $m=500\,g$ est accroché à un ressort de constante de raideur $k=100N/m$ et repose sans frottement sur une table inclinée d'un angle $\alpha=30^{\circ}$ par rapport à l'horizontale.

L'axe du ressort est parallèle au plan incliné (voir figure ci-dessous)

5.1 En choisissant le solide $(S)$ comme système, reprendre et représenter qualitativement (sans soucis d'échelle) toutes les forces extérieures au système. (01 pt)

5.2 Quelle force est à la fois une force répartie et une force de contact. (0.5 pt)

5.3 Calculer l'intensité de la force de pesanteur. (0.5 pt)

5.4 Sachant que la somme vectorielle des forces est égale au vecteur nul, déterminer l'intensité $R$ de la réaction de la table ainsi que l'allongement $x$ du ressort. (02 pts)

$$\text{Durée : }3h$$

Auteur:

Sidy Ndiaye

Commentaires

EDOUARD (non vérifié)

lun, 03/22/2021 - 21:33