Vous êtes ici

Corrigé Bac Maths S2 1er groupe 2011

Classe:

Terminale

Exercice 1

I. 1)

$Z$ est écrit sous forme algébrique,

$X$ est sa partie réelle et

$y$ sa partie imaginaire (ou

$\mathrm{i}y).$

2) Son module est

$|Z|=\sqrt{x^{2}+y^{2}}.$

$\cos\alpha=\dfrac{\Re e(Z)}{|Z|}\:,\quad\sin\alpha=\dfrac{\Im m(Z)}{|Z|}$

4) Soit

$O(0)\;,\ Z’- Z_{O}=\mathrm{e}^{\mathrm{i}\theta}\left(Z-Z_{O}\right)$

$\boxed{Z'=Z\mathrm{e}^{\mathrm{i}\theta}}$

II.

$(E) : \dfrac{1}{2}Z^{2}+4Z\sqrt{3}+32=0$

$\begin{array}{rcl} \Delta'&=&(2\sqrt{3})^{2}-16\\ \\&=&-4\\ \\&=&(2\mathrm{i})^{2}\end{array}$

Donc,

$\Delta'=(2\mathrm{i})^{2}$

Par suite,

$Z_{1}=\dfrac{-2\sqrt{3}-2\mathrm{i}}{\dfrac{1}{2}}\$ et

$\ Z_{2}=\dfrac{-2\sqrt{3}+2\mathrm{i}}{\dfrac{1}{2}}$

On obtient :

$\boxed{Z_{1}=-4\sqrt{3}-4\mathrm{i}}\$ et

$\ \boxed{Z_{2}=-4\sqrt{3}+4\mathrm{i}}$

$a=-4\sqrt{3}-4\mathrm{i}\;,\ b=-4\sqrt{3}+4\mathrm{i}$

On a :

$OA=|a|=8\;,\ OB=|b|=8\$ et

$\ AB=|8\mathrm{i}|=8.$ Donc

$OAB$ est un triangle équilatéral.

$\begin{array}{rcl} Z_{D}&=&Z_{C}\mathrm{e}^{\mathrm{i}\tfrac{\pi}{3}}\\ \\&=&\left(\dfrac{1}{2}+\mathrm{i}\dfrac{\sqrt{3}}{2}\right)\left(\sqrt{3}+\mathrm{i}\right)\\ \\&=&\dfrac{1}{2}\mathrm{i}(\sqrt{3}-\mathrm{i})(\sqrt{3}+\mathrm{i})\\ \\&=&\dfrac{1}{2}\mathrm{i}\times 4\end{array}$

$\boxed{Z_{D}=2\mathrm{i}}$

$G$ = barycentre du système

$\{(O\;,\ 1)\;,\ (D\;,\ -1)\;,\ (B\;,\ -1)\}.$

$\begin{array}{rcl} g&=&\dfrac{1.Z_{0}-1.Z_{D}-1.Z_{B}}{-1}\\ \\&=&Z_{D}+Z_{B}\\ \\&=&2\mathrm{i}+(-4\sqrt{3}+4\mathrm{i})\\ \\&=&-4\sqrt{3}+6\mathrm{i}\end{array}$

$\boxed{g=-4\sqrt{3}+6\mathrm{i}}$

b) Plaçons les points

$A\;,\ B\;,\ C\$ et

$\ G$ dans le repère

$(O\;,\ \vec{u}\;,\ \vec{v})$

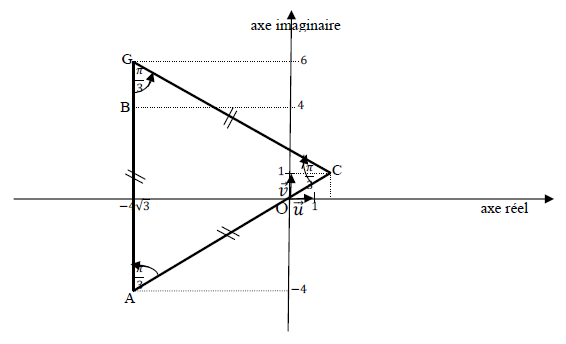
On vérifie que :

$\dfrac{c-g}{a-g}=\dfrac{1}{2}+\mathrm{i}\dfrac{\sqrt{3}}{2}$

Donc,

$\left\lbrace\begin{array}{rcl} |c-g|&=&|a-g|\\ \\arg\left(\dfrac{c-g}{a-g}\right)&=&\dfrac{\pi}{3}\;[2\pi]\end{array}\right.$

D'où :

$\left\lbrace\begin{array}{rcl} GA&=&GC\\ \\(\overrightarrow{GA}\;,\ \overrightarrow{GC})&=&\dfrac{\pi}{3}\; [2\pi]\end{array}\right.$

Donc,

$GAC$ est un triangle équilatéral direct.

Exercice 2

$p(A)=\dfrac{Card\;A}{Card\;\Omega}\;,\quad p(A/B)=\dfrac{Card\;(A\cap B)}{Card\;B}$

$p(A)=p(A\cap\overline{B})+p(A\cap B)$ , car

$A=(A\cap\overline{B})\cup(A\cap B)\$ et

$\ A\cap\overline{B}\$ et

$\ A\cap B$ sont deux événements incompatibles.

II. 1)

$p(D_{1})=1\;,\quad p(D_{n+1}/D_{n})=\dfrac{2}{9}\;,\quad p(D_{n+1}/\overline{D}_{n})=\dfrac{5}{6}$

$p(D_{n+1})=p_{n+1}$

$p(D_{n+1})=p(D_{n+1}\cap D_{n})+p(D_{n+1}\cap\overline{D}_{n})\$ or,

$p(D_{n+1})=p_{n+1}$

Donc,

$p_{n+1}=p(D_{n})p(D_{n+1}/D_{n})+p(\overline{D}_{n})p(D_{n+1}/\overline{D}_{n})$

D'où,

$p_{n+1}=\dfrac{2}{9}p_{n}+(1-p_{n})\dfrac{5}{6}$

Ainsi,

$\boxed{p_{n+1}=-\dfrac{11}{18}p_{n}+\dfrac{5}{6}}$

$U_{n}=6p_{n}-\dfrac{90}{29}\;;\ n\in\mathbb{N}^{*}$

$\begin{array}{rcl} U_{n}&=&6p_{n}-\dfrac{90}{29}\\ \\&=&6\left(p_{n}-\dfrac{15}{29}\right)\end{array}$

Donc,

$U_{n+1}=6\left(p_{n+1}-\dfrac{15}{29}\right)$

En remplaçant

$p_{n+1}$ par son expression, on a :

$\begin{array}{rcl} U_{n+1}&=&6\left(-\dfrac{11}{18}p_{n}+\dfrac{5}{6}-\dfrac{15}{29}\right)\\ \\&=&6\left(-\dfrac{11}{18}p_{n}+\dfrac{55}{6\times 29}\right)\\ \\&=&6\times\dfrac{-11}{18}\left(p_{n}-\dfrac{55}{11}\times\dfrac{18}{6\times 29}\right)\\ \\&=&-\dfrac{11}{18}\left(6p_{n}-\dfrac{90}{29}\right)\end{array}$

Donc,

$\boxed{q=-\dfrac{11}{18}}$

$U_{n}=U_{1}\times q^{n-1}$

$\begin{array}{rcl} U_{1}&=&6p_{1}-\dfrac{90}{29}\\ \\&=&6-\dfrac{90}{29}\\ \\&=&\dfrac{84}{29}\end{array}$

Donc,

$\boxed{U_{1}=\dfrac{84}{29}}$

D'où :

$\boxed{U_{n}=\dfrac{84}{29}\times\left(\dfrac{-11}{18}\right)^{n-1}\;;\ n\in\mathbb{N}^{*}}$

$p_{n}=\dfrac{1}{6}\left(U_{n}+\dfrac{90}{29}\right)$

Par suite,

$\boxed{p_{n}=\dfrac{1}{6}\left[\dfrac{84}{29}\times\left(\dfrac{-11}{18}\right)^{n-1}+\dfrac{90}{29}\right]}$

c) Soit

$q_{20}$ la probabilité que la ville soit sans délestage le

$20^{eme}$ jour.

Alors,

$q_{20}=1-p_{20}$

Ainsi,

$\boxed{q_{20}\cong 6.483}$ à

$10^{-3}$ prés par défaut.

Problème

$f(x)=\dfrac{3(x-1)^{3}}{3x^{2}+1}$

Soit

$D_{f}$ le domaine de définition de la fonction

$f\;,$

$D_{f}=\mathbb{R}\$ car

$\ 3x^{2}+1\neq 0$ pour tout

$x\in\mathbb{R}$

$\lim_{x\rightarrow -\infty}f(x)=-\infty\qquad\lim_{x\rightarrow +\infty}f(x)=+\infty$

$x\mapsto(x-1)^{3}$ est dérivable sur

$\mathbb{R}$ comme puissance d'une fonction dérivable sur

$\mathbb{R}.$

D'où par produit

$x\mapsto 3(x-1)^{3}$ est dérivable sur

$\mathbb{R}$

$x\mapsto 3x^{2}+1$ dérivable sur

$\mathbb{R}$ et

$3x^{2}+1\neq 0$ pour tout réel ; par quotient

$x\mapsto f(x)$ dérivable sur

$\mathbb{R}.$

Calculons

$f'(x)$

$\begin{array}{rcl} f'(x)&=&3\dfrac{3(x-1)^{2}(3x^{2}+1)-(x-1)^{3}(6x)}{(3x^{2}+1)^{2}}\\ \\&=&3(x-1)^{2}\left[\dfrac{3(3x^{2}+1)-(x-1)(6x)}{(3x^{2}+1)^{2}}\right]\\ \\&=&3(x-1)^{2}\left[\dfrac{9x^{2}+3-6x^{2}+6x}{(3x^{2}+1)^{2}}\right]\\ \\&=&\dfrac{9(x-1)^{2}(x+1)^{2}}{(3x^{2}+1)^{2}}\end{array}$

Ainsi,

$\boxed{f'(x)=\dfrac{9(x-1)^{2}(x+1)^{2}}{(3x^{2}+1)^{2}}}$

Pour tout réel

$x\;;\ f'(x)\geq 0$

Tableau de variation de

$f$

$\begin{array}{|c|lcccccr|}\hline x&-\infty&&-1&&1&&+\infty\\ \hline f'(x)&&+&0&+&0&+&\\ \hline&&&&&&&+\infty\\&&&\vdots&&\vdots&\nearrow&\\f&&&\vdots&&0&&\\&&&\vdots&\nearrow&\vdots&&\\&&&-6&&\vdots&&\\&&\nearrow&\vdots&&\vdots&&\\&-\infty&&&&&&\\ \hline\end{array}$

$f$ continue et strictement croissante sur

$\mathbb{R}$ donc

$f$ réalise une bijection continue de

$\mathbb{R}$ sur

$f(\mathbb{R})=\mathbb{R}$ et

$1\in\;f(\mathbb{R}).$

Donc, d'après le corollaire du théorème des valeurs intermédiaires l'équation

$f(x)=1$ admet une

solution unique

$\alpha\in\mathbb{R}$

Montrons

$3<\alpha<4.$

La restriction de

$f$ à

$[3\;;\ 4]$ est une bijection continue et

$f(3)<1<f(4)$ donc, l'équation

$f(x)=1$ admet une solution

$\alpha\in]3\;;\ 4[.$

II.

$g(x)=\dfrac{3(\ln|x|-1)^{3}}{3\ln^{2}|x|+1}$

1) a)

$g(x)$ existe si, et seulement,

$\left\lbrace\begin{array}{rcl} x&\neq&0\\3\ln^{2}|x|+1&\neq&0\end{array}\right.$

Or,

$3\ln^{2}|x|+1\neq 0$ pour tout réel

$x\neq 0$

D'où :

$\boxed{D_{g}=\mathbb{R}^{*}}$

$g(x)=\dfrac{3(\ln|x|-1)^{3}}{3(\ln|x|)^{2}+1}$

$g(x)=f(\ln|x|)$ en posant

$h(x)=\ln|x|$ , on a :

$\boxed{g(x)=(f\circ h)(x)\;;\ x\neq 0}$

$D_{g}=\mathbb{R}^{*}$

Soit

$x\in D_{g}$ donc

$-x \in D_{g}$ (car

$\mathbb{R}^{*}$ stable par passage à l'opposé)

$g(-x)=f(h(-x))$ or

$h$ est paire

$\Rightarrow h(-x)=x$

D'où :

$\boxed{g(-x)=g(x),\;x\neq 0}$

Ainsi,

$g$ est paire sur

$D_{g}.$

$D_{E}=]0\;,\ +\infty[$

$x>0$ donc,

$h(x)=\ln x\$ or

$\ k(x)=f(h(x))$

$\lim_{x\rightarrow 0^{+}}h(x)=-\infty\quad\text{et}\quad\lim_{x\rightarrow -\infty}f(x)=-\infty$

Par composée, on obtient :

$\boxed{\lim_{x\rightarrow 0^{+}}k(x)=-\infty}$

$\lim_{x\rightarrow +\infty}h(x)=+\infty\quad\text{et}\quad\lim_{x\rightarrow +\infty}f(x)=+\infty$

Par composée, on obtient :

$\boxed {\lim_{x\rightarrow +\infty}k(x)=+\infty}$

Étude des branches infinies en

$+\infty$

Soit

$k(x)=\dfrac{3(\ln x-1)^{3}}{3\ln^{2}x+1}$ alors :

$\begin{array}{rcl}\text{Pour } x>0\;;\ \dfrac{k(x)}{x}&=&\dfrac{3(\ln^{3}x-3\ln x^{2}+3\ln x-1)}{x(3\ln^{2}x+1)}\\ \\&=&\dfrac{3\ln x}{x}\dfrac{\left[1-\dfrac{3}{\ln x}+\dfrac{3}{\ln x^{2}}-\dfrac{1}{\ln x^{3}}\right]}{\left[3+\dfrac{1}{\ln^{2}x}\right]}\end{array}$

Ainsi,

$\lim_{x\rightarrow +\infty}\dfrac{k(x)}{x}=0$

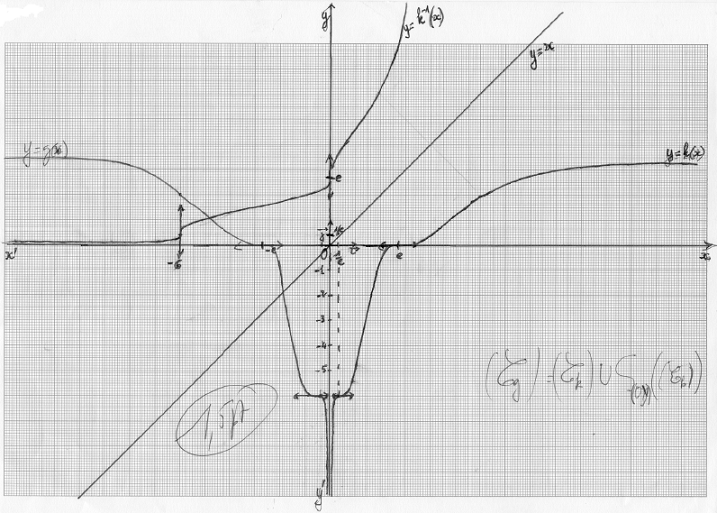
D'où,

$(\mathcal{C}_{k})$ admet en

$+\infty$ une branche parabolique de direction celle de l'axe des abscisses.

2)a) On a :

$k(x)=(f\circ h)(x)$

En utilisant la forme de la dérivation d'une forme composée on obtient :

$\begin{array}{rcl} k'(x)&=&h'(x)\times f'(h(x))\\ \\&=&\dfrac{1}{x}f'(h(x))\end{array}$

Donc,

$\boxed{k'(x)=\dfrac{1}{x}f'(h(x))}$

$k'(x)$ garde un signe positif sur

$]0\;,\ +\infty[$ mais

$k’(x)$ s'annule en

$x$ vérifiant

$\ln x-1=0\$ ou

$\ \ln x+1=0$

c'est à dire ;

$x=\mathrm{e}\$ ou

$\ x=\dfrac{1}{\mathrm{e}}$

Tableau de variation de

$k$

$\begin{array}{|c|lcccccr|}\hline x&0&&1/\mathrm{e}&&\mathrm{e}&&+\infty\\ \hline k'(x)&|&+&0&+&0&+&\\ \hline&|&&&&&&+\infty\\&|&&\vdots&&\vdots&\nearrow&\\k&|&&\vdots&&0&&\\&|&&\vdots&\nearrow&\vdots&&\\&|&&-6&&\vdots&&\\&|&\nearrow&\vdots&&\vdots&&\\&-\infty&&&&&&\\ \hline\end{array}$

$k\left(\dfrac{1}{\mathrm{e}}\right)=\dfrac{3(-1-1)^{3}}{3+1}=-6$

$\begin{array}{rcrcl} k(x)=0&\Leftrightarrow&3(\ln x-1)^{3}&=&0\\ \\&\Leftrightarrow&\ln x-1&=&0\\ \\&\Leftrightarrow&\ln x&=&1\\ \\&\Leftrightarrow&x&=&\mathrm{e}\end{array}$

$(\mathcal{C}_{k})$ coupe l'axe des abscisses en

$A(\mathrm{e}\;,\ 0)$

$\boxed{\begin{array}{l}\text{Si}\quad x\in\; ]0\;,\ \mathrm{e}[\;,\ k(x)<0\\ \\ \text{Si}\quad x\in\; ]\mathrm{e}\;,\ +\infty\;,\ k(x)>0\\ \\ \text{Si}\quad x=\mathrm{e}\;,\ k(x)=0\end{array}}$

3) a)

$k$ est continue et strictement croissante sur

$]0\;,\ +\infty[$ par composée de deux fonctions continue et strictement croissante. D'où,

$k$ réalise une bijection de

$]0\;,\ +\infty[$ sur

$\mathbb{R}.$

Par suite,

$k(]0\;;\ +\infty[)=\mathbb{R}$

Ainsi,

$J=\mathbb{R}$

Commentaires

Anonyme (non vérifié)

lun, 05/31/2021 - 23:03

Permalien

Stdtdtr

répondre

Ajouter un commentaire

form.antibot { display: none !important; } You must have JavaScript enabled to use this form.

Vous êtes ici

Corrigé Bac Maths S2 1er groupe 2011

Formulaire de recherche

Exercice 1

Exercice 2

Problème

Commentaires

Stdtdtr

Ajouter un commentaire

Plain text