Bac Maths, ES Polynésie 21 juin 2019
Exercice 1 4 points
Commun à tous les candidats
Pour chacune des questions suivantes, une seule des quatre propositions est exacte. Aucune justification n'est demandée.
Une bonne réponse rapporte un point.
Une mauvaise réponse, plusieurs réponses ou l'absence de réponse à une question ne rapporte ni n'enlève de point.
Pour répondre, recopier sur la copie le numéro de la question et indiquer la réponse choisie.
1) On considère la fonction $f$ définie et dérivable sur $]0\ ;\ +\infty[$ d'expression
$f(x)=-1.5x^{2}+x^{2}\ln(x).$
La fonction dérivée de $f$ est donnée pour tout $x$ de $]0\ ;\ +\infty[$ par :
a) $f'(x)=-x+1$
b) $f'(x)=2x\ln(x)-2x$
c) $f'(x)=-3x+2$
d) $f'(x)=-x\ln(x)-0.5x$
2) Entre $2006$ et $2018$, dans un restaurant universitaire, le prix d'un repas est passé de $2$ euros à $3.50$ euros en augmentant chaque année de $x\%.$
Parmi ces valeurs, la valeur la plus proche de $x$ est :
a) $6.25$
b) $4.77$
c) $14.58$
d) $0.85$
3) Un adolescent joue à un jeu dont les parties successives sont indépendantes.
À chaque partie, il a une chance sur $25$ de sortir vainqueur.
Après $13$ parties, à $10^{-3}$ près, la probabilité qu'il ait gagné au moins une fois est :
a) $0.588$
b) $0.412$
c) $0.025$
d) $0.975$
4) On considère une fonction $g$ définie sur $\mathbb{R}$, dont la courbe représentative $\mathcal{C_{g}}$ est donnée ci-dessous.
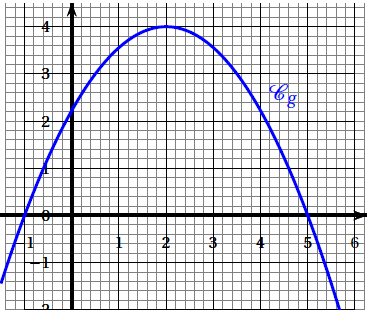
La fonction $g$ admet une primitive sur $\mathbb{R}$ notée $G.$
La fonction $G$ est :
a) convexe sur l'intervalle $[−1\ ;\ 5].$
b) concave sur l'intervalle $[-1\ ;\ 5].$
c) croissante sur l'intervalle $[2\ ;\ 5].$
d) décroissante sur l'intervalle $[2\ ;\ 5]$
Exercice 2 5 points
Commun à tous les candidats
Les parties sont indépendantes
Une entreprise vend des téléviseurs.
Pour tout évènement $E$, on note $E$ l'évènement contraire de $E$ et $p(E)$ sa probabilité
Partie A
Une étude a montré que ces téléviseurs peuvent rencontrer deux types de défauts : un défaut sur la dalle, un défaut sur le condensateur.
L'étude indique que :
$\bullet\ $ $3\%$ des téléviseurs présentent un défaut sur la dalle et parmi ceux-ci $2\%$ ont aussi un défaut sur le condensateur.
$\bullet\ $ $5\%$ des téléviseurs ont un défaut sur le condensateur.
On choisit au hasard un téléviseur et on considère les évènements suivants :
$\bullet\ $ $D$ : « le téléviseur a un défaut sur la dalle » ;
$\bullet\ $ $C$ : « le téléviseur a un défaut sur le condensateur
1) Les résultats seront approchés si nécessaire à $10^{-4}$ près.
a) Exprimer les trois données numériques de l'énoncé sous forme de probabilités.
b) Recopier l'arbre ci-dessous et compléter uniquement les pointillés par les probabilités
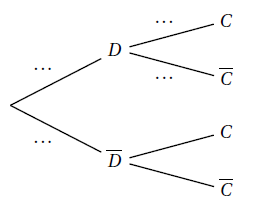
c. Calculer la probabilité $p(D\cap C)$ de l'événement $D\cap C.$
d)Le téléviseur choisi a un défaut sur le condensateur.
Quelle est alors la probabilité qu'il ait un défaut sur la dalle?
e)La probabilité que le téléviseur choisi ait un défaut sur le condensateur mais pas de défaut sur la dalle vaut $0.0494.$
Justifier cette affirmation
2. Les résultats seront approchés à $10^{-2}$ près.
On note $T$ la variable aléatoire qui, à chaque téléviseur prélevé, associe le temps exprimé en mois avant la première panne.
On admet que $T$ suit la loi normale d'espérance $\mu=84$ et d'écart
a) Donner la probabilité qu'un téléviseur tombe en panne pour la première fois après $72$ mois d'utilisation.
b) Quelle est la probabilité que la première panne arrive entre $6$ années et $8$ années d'utilisation.
c) Le téléviseur n'a pas eu de panne après $6$ années d'utilisation.
Quelle est la probabilité qu'il tombe en panne avant $8$ années d'utilisation ?
Partie B
Afin de satisfaire davantage de clients, l'entreprise décide d'apporter des améliorations à son service d'assistance.
Après quelques mois de mise en place du nouveau service, elle affirme que $90\%$ des clients sont maintenant satisfaits.
Un service de contrôle indépendant veut vérifier cette affirmation.
Pour cela il interroge au hasard $300$ clients. Parmi eux, $265$ affirment être satisfaits.
Les résultats de cette étude remettent-ils en cause l'affirmation de l'entreprise?
Justifier la réponse
Exercice 3 5 points
Candidats n'ayant pas suivi l'enseignement de spécialité
Sur un site de vente en ligne, Antoine a commandé une machine à café à capsules.
1) Chaque capsule achetée à l'unité coûte $0.60$ euro.
Une offre permet d'acquérir $150$ capsules au prix de $60$ euro.
De quel pourcentage de réduction bénéficie-t-on grâce à l'offre par rapport à un achat à l'unité ?
2) Au $1^{er}$ janvier $2017$, on comptait $60\ 000$ utilisateurs de cette machine à café.
On estime que chaque mois, $10\%$ des propriétaires cessent de l'utiliser mais on compte $24\ 000$ nouveaux utilisateurs.
a) Expliquer pourquoi le nombre d'utilisateurs de cette machine à café $n$ mois après le $1^{er}$ janvier $2017$, peut être modélisé par la suite $(u_{n})$ définie par :
$u_{0}=60\ 000$ et $u_{n+1}=0.9u_{n}+24\ 000$
b) On considère la suite $(v_{n})$ définie, pour tout entier naturel $n$, par : $v_{n}=u_{n}=240000.$
Démontrer que la suite $(v_{n})$ est une suite géométrique dont on précisera le premier terme et la raison.
3) a) $n$ étant un entier naturel, exprimer $v_{n}$ en fonction de $n.$
b) En déduire que pour tout entier naturel $n$, $u_{n}=240000-180000\times\,0.9^{n}.$
4) Au bout de combien de mois le nombre d'utilisateurs de cette machine à café dépassera-t-il pour la première fois $230\ 000$ ?
5) L'entreprise qui fabrique cette machine à café prétend qu'elle touchera un certain mois plus de $250\ 000$ utilisateurs.
Que penser de cette affirmation ?
Exercice 3 5 points
Candidats ayant suivi l'enseignement de spécialité
Deux grossistes $A$ et $B$ se partagent la clientèle d'un liquide industriel.
On suppose que le nombre total de clients reste fixe d'une année sur l'autre.
En $2017$, $45\%$ des clients se fournissaient chez le grossiste $A$ et $55\%$ chez le grossiste $B.$
D'une année sur l'autre, $6\%$ des clients du grossiste $A$ deviennent clients du grossiste $B$ tandis que le grossiste $B$ conserve $86\%$ de ses clients.
Chaque année, on choisit au hasard un client ayant acheté le liquide.
Pour tout entier naturel $n$ on note :
$\bullet\ $ $a_{n}$ la probabilité qu'il soit client du grossiste $A$ en $(2017+n)$,
$\bullet\ $ $b_{_{n}}$ la probabilité qu'il soit client du grossiste $B$ en $(2017+n).$
Pour tout entier naturel $n$, on note $P_{n}=(a_{n}\quad b_{n})$ la matrice ligne représentant l'état probabiliste de l'année $(2017+n).$
On rappelle que $a_{n}+b_{n}=1.$
On a donc $P_{0}=(0.45\quad 0.55).$
1) Représenter cette situation par un graphe probabiliste dans lequel les sommets $A$ et $B$ correspondent aux noms des grossistes.
2) a) Donner la matrice de transition $T$ associée à ce graphe (les sommets seront rangés par ordre alphabétique).
b) Quelle sera, exprimée en pourcentage, la répartition prévisible des ventes entre ces deux grossistes en $2020$ ?
Justifier la réponse.
On arrondira les résultats à $0.1\%$ près.
3) On admet que pour tout entier naturel $n$, $a_{n+1}=0.8a_{n}+0.14.$
a) On pose pour tout naturel $n$ : $u_{n}=a_{n}-0.7.$
Démontrer que la suite $(u_{n})$ est une suite géométrique dont on précisera le premier terme et la raison.
b) En déduire que pour tout entier naturel $n$, $a_{n}=−0.25\times 0.8^{n}+0.7.$
c) Quelle part du marché, exprimée en pourcentage, le grossiste $A$ peut-il espérer à long terme ?
Justifier la réponse.
d) À partir de quelle année le grossiste $A$ détiendra t-il plus de $65\%$ du marché ?
Exercice 4 6 points
Commun à tous les candidats
Les deux parties de cet exercice sont indépendantes
Partie A
Une entreprise produit chaque année entre $100$ et $900$ pneus pour tracteurs.
On considère la fonction $f$ définie sur l'intervalle $[1\ ;\ 9]$ par :
$$f(x)=0.5x^{2}-7x+14+6\ln(x).$$
On admet que la fonction $f$ modélise le coût moyen annuel de fabrication d'un pneu, exprimé en centaines d'euros, pour $x$ centaines de pneus produits.
1) La fonction $f$ est dérivable sur l'intervalle $[1\ ;\ 9]$ et on note $f′$ sa fonction dérivée.
Démontrer que pour tout réel $x$ de l'intervalle $[1\ ;\ 9]$ on a : $f'(x)=\dfrac{x^{2}-7x+6}{x}.$
2) a) Justifier les variations suivantes de la fonction $f$ sur l'intervalle $[1\ ;\ 9]$ :
$$\begin{array}{|c|lcr|} \hline x&1&6&9\\ \hline \text{Variation de }f&\searrow&&\nearrow\\ \hline \end{array}$$
b) Justifier que, sur l'intervalle $[1\ ;\ 9]$, l'équation $f(x)=5$ admet une unique solution $\alpha.$
c) Donner un encadrement au centième près de $\alpha.$
d) On considère l'algorithme ci-dessous :
$$\boxed{X\leftarrow 1\\\\Y\leftarrow 7.5\\\\\text{Tant que }Y>5\\\\X\leftarrow X+0.01\\\\Y\leftarrow 0.5X^{2}-7X+14+6\ast\ln(X)\\\\\text{Fin Tant que}}$$
À la fin de l'exécution de l'algorithme, quelle valeur numérique contient la variable $X$ ?
3) Pour quelle quantité de pneus,le coût moyen annuel de fabrication d'un pneu est-il minimal ?
À combien s'élève-t-il ?
Partie B
Cette même entreprise envisage la fabrication de semoirs (gros matériel agricole).
On admet que la fonction $g$ définie sur l'intervalle $[0\ ;\ 100]$ par
$$g(x)=2x-1+\mathrm{e}^{0.05x}$$
modélise le coût de fabrication, exprimé en centaines d'euros, de $x$ semoirs.
1) Donner une primitive $G$ de la fonction $g$ sur l'intervalle $[0\ ;\ 100].$
2) Calculer la valeur moyenne de la fonction $g$ sur l'intervalle $[0\ ;\ 100].$
3) Interpréter ce résultat dans le contexte de l'exercice.

Ajouter un commentaire