Bac Maths, ES/L Métropole - La Réunion $13$ septembre $2019$
Exercice 1 (5 points)
Commun à tous les candidats
En $2018$, la France comptait environ $225\ 000$ médecins actifs.
On prévoit que chaque année, $4\%$ des médecins cessent leur activité tandis que $8\ 000$ nouveaux médecins s'installent.
Pour étudier l'évolution du nombre de médecins en activité dans les années à venir, on modélise la situation par une suite $(u_{n}).$
Pour tout entier naturel $n$, le terme un représente le nombre de médecins en $2018+n$, exprimé en millier.
1) Donner $u_{0}$ et calculer $u_{1}.$
2) Justifier que, pour tout entier naturel $n$, on a : $u_{n+1}=0.96u_{n}+8.$
3) Recopier et compléter l'algorithme suivant afin qu'il calcule, selon cette modélisation, le nombre de médecins que compterait la France en $2031.$
$$\boxed{U\leftarrow 225\\\text{Pour N allant de}\ldots\text{à}\ldots\\U\leftarrow\ldots\\\text{Fin Pour}}$$
4) On considère la suite $(v_{n})$ définie par, pour tout entier naturel $n$ :
$$v_{n}=u_{n}-200.$$
a) Montrer que la suite $(v_{n})$ est géométrique de raison $0.96.$
Préciser son terme initial.
b) Exprimer, pour tout entier naturel $n$, $v_{n}$ en fonction de $n.$
c) En déduire que pour tout entier naturel $n$, $u_{n}=25\times 0.96^{n}+200.$
5) On admet que pour tout entier naturel $n$ : $u_{n+1}-u_{n}=-0.96^{n}.$
a) En déduire le sens de variation de la suite $(u_{n}).$
b) Interpréter le résultat dans le contexte de l'exercice.
6) a) Résoudre dans l'ensemble des entiers naturels l'inéquation
$$25\times 0.96^{n}+200<210.$$
b) Interpréter le résultat dans le contexte de l'exercice.
Exercice 2 (5 points)
Commun à tous les candidats
Pour chacune des cinq affirmations suivantes, indiquer si elle est vraie ou fausse en justifiant la réponse.
Il est attribué un point par réponse exacte correctement justifiée.
Une réponse non justifiée n'est pas prise en compte.
Une absence de réponse n'est pas pénalisée.
1) Un laboratoire reçoit un lot de prélèvements sanguins et réalise des analyses sur ce lot.
On choisit un prélèvement au hasard et on note $X$ la variable aléatoire égale au taux d'hémoglobine dans ce prélèvement.
On admet que $X$ suit une loi normale d'espérance $\mu=12.$
Pour tout évènement $A$, on note $P(A)$ sa probabilité.
Affirmation A :
$P(X>14)=P(X<11).$
2) Soit $f$ la fonction définie sur $\mathbb{R}$ par $f(x)=5\mathrm{e}^{-0.3x} +1.$
Affirmation B :
La valeur moyenne de $f$ sur l'intervalle $[0\ ;\ 5]$ est égale à $3.6$, arrondie au dixième.
3) Un comité d'entreprise souhaite mettre à disposition des salariés une salle de sport.
Son directeur affirme qu'un tiers des employés serait intéressé par une telle salle.
On réalise un sondage dans lequel on interroge $180$ employés au hasard, parmi lesquels $72$ se déclarent intéressés.
Affirmation C :
Ce sondage remet en question l'affirmation du directeur.
4) Soit $f$ une fonction définie et dérivable sur $\mathbb{R}$, dont la courbe représentative est donnée ci-dessous.
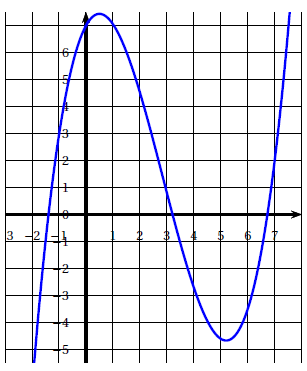
Soit $F$ une primitive de $f$ sur $\mathbb{R}$
Affirmation D :
La fonction $F$ est convexe sur $[1\ ;\ 3].$
5) Soit $f$ la fonction définie sur $[0\ ;\ 1]$ par $f(x)=3x^{2}-4x+2.$
Affirmation E :
$f$ est une fonction de densité sur $[0\ ;\ 1].$
Exercice 3 (5 points)
Commun à tous les candidats
La courbe $\mathcal{C}_{f}$ ci-dessous est la courbe représentative d'une fonction $f$ définie et deux fois dérivable sur l'intervalle $[1.1\ ;\ 8].$
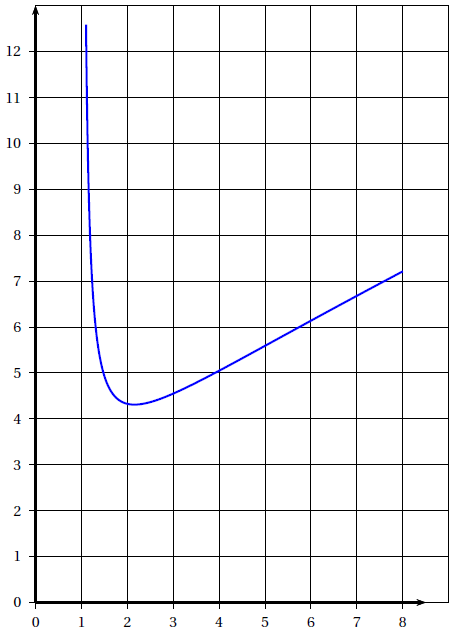
Les parties $A$ et $B$ peuvent être traitées de manière indépendante.
Partie A : étude graphique
1) Donner une valeur approchée du minimum de la fonction $f$ sur l'intervalle $[1.1\ ;\ 8].$
2) Quel est le signe de $f'(5)$ ?
Justifier.
3) Encadrer l'intégrale $$\int_{2}^{4}f(x)\mathrm{d}x$$ par deux entiers consécutifs.
4) La fonction $f$ est-elle convexe sur $[1.1\ ;\ 8]$ ?
Justifier.
Partie B : étude analytique
On admet que $f$ est la fonction définie sur l'intervalle $[1.1\ ;\ 8]$ par :
$$f(x)=\dfrac{2x-1}{\ln(x)}$$
1) Montrer que, pour tout réel $x$ de l'intervalle $[1.1\ ;\ 8]$, on a :
$$f'(x)=\dfrac{2\ln(x)-2+\dfrac{1}{x}}{(\ln(x))^{2}}$$
2) Soit $h$ la fonction définie sur $[1.1\ ;\ 8]$ par : $$h(x)=2\ln(x)-2+\dfrac{1}{x}.$$
a) Soit $h'$ la fonction dérivée de $h$ sur l'intervalle $[10.1\ ;\ 8].$
Montrer que, pour tout réel $x$ de l'intervalle $[1.1\ ;\ 8]$,
$$h'(x)=\dfrac{2x-1}{x^{2}}$$
b) En déduire les variations de la fonction $h$ sur l'intervalle $[1.1\ ;\ 8].$
c) Montrer que l'équation $h(x)=0$ admet une unique solution $\alpha$ sur l'intervalle $[1.1\ ;\ 8].$
Donner un encadrement de $\alpha$ par deux entiers consécutifs.
3) Déduire des résultats précédents le signe de $h(x)$ sur l'intervalle $[1.1\ ;\ 8].$
4) À l'aide des questions précédentes, donner les variations de $f$ sur $[1.1\ ;\ 8].$
Exercice 4 (5 points)
Candidats de E, S n'ayant pas suivi la spécialité ou candidats de L
Pour tous évènements $E$ et $F$, on note $\overline{E}$ l'évènement contraire de $E$, $P(E)$ la probabilité de $E$ et, si $F$ est de probabilité non nulle, $P_{F}(E)$ la probabilité de $E$ sachant $F.$
On arrondira les résultats au millième si besoin.
Partie A
Pour mieux cerner le profil de ses clients, une banque réalise un sondage qui permet d'établir que :
$\bullet\ $ $53\%$ de ses clients ont plus de $50$ ans ;
$\bullet\ $ $32\%$ de ses clients sont intéressés par des placements dits risqués ;
$\bullet\ $ $25\%$ de ses clients de plus de $50$ ans sont intéressés par des placements dits risqués.
On choisit au hasard un client de cette banque et on considère les évènements suivants :
$\bullet\ $ $A$ : « Le client a plus de $50$ ans » ;
$\bullet\ $ $R$ : « Le client est intéressé par des placements dits risqués ».
1) Donner $P(R)$ et $P_{A}(R).$
2) Représenter la situation par un arbre pondéré.
Cet arbre pourra être complété par la suite.
3) Montrer que la probabilité que le client ait plus de $50$ ans et soit intéressé par des placements dits risqués est $0.1325.$
4) Sachant que le client est intéressé par des placements dits risqués, quelle est la probabilité qu'il ait plus de $50$ ans ?
5) Calculer $P\left(\overline{A}\cap R\right)$ puis en déduire $P_{\overline{A}}(R).$
Interpréter les deux résultats obtenus.
Partie B
L'une des agences de cette banque charge ses conseillers de proposer un placement dit risqué, $R_{1}$ à tous ses clients.
Elle promet à ses conseillers une prime de $150$ euro s'ils convainquent au moins $10$ clients d'effectuer ce placement en un mois et une prime supplémentaire de $150$ s'ils convainquent au moins $15$ clients d'effectuer ce placement en un mois.
L'une des conseillères de cette banque, Camille, reçoit $45$ clients ce mois-ci.
1) On admet que la probabilité que Camille réussisse à placer ce produit auprès de l'un de ses clients est de $0.23$ et que la décision d'un client est indépendante de celles des autres clients.
a) Déterminer la probabilité que Camille place le produit $R_{1}$ auprès de $10$ clients exactement ce mois-ci.
b) Calculer la probabilité que Camille ait $300$ euro de prime.
c) Montrer que la probabilité que Camille ait $150$ euro exactement de prime est environ de $0.532.$
2) Le placement $R_{1}$ a rapporté $30\%$ d'intérêt sur les $5$ dernières années.
Calculer le taux d'intérêt annuel moyen du placement $R_{1}$ sur ces $5$ dernières années.
Exercice 4 (5 points)
Candidats de E, S ayant suivi la spécialité
Deux amis, Louisa et Antoine, passent la journée dans un parc d'attraction.
Le plan du parc est donné par le graphe ci-dessous.
Les arêtes de ce graphe représentent les allées du parc et les sommets correspondent aux intersections de ces allées.
On a pondéré les arêtes de ce graphe par les temps de parcours en minutes.
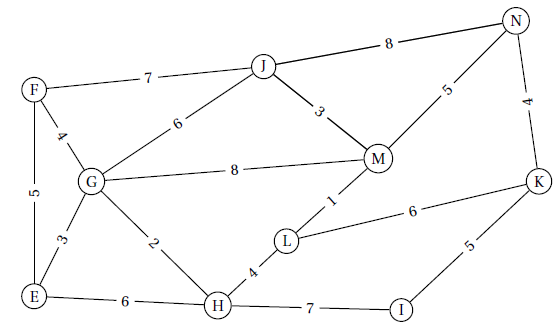
1) Le graphe est-il convexe ?
Justifier.
2) Antoine prétend avoir trouvé un itinéraire permettant d'emprunter chaque allée une et une seule fois mais Louisa lui répond que c'est impossible.
Lequel des deux a raison ?
Justifier la réponse.
3) On considère la matrice $M$ ci-dessous $(a$, $b$ et $c$ sont des entiers$)$
$$M=\begin{pmatrix}\\ 0&1&1&1&a&0&0&0&0&0\\ 1&0&1&0&0&1&0&0&0&0\\ 1&1&0&1&0&1&0&0&1&0\\ 1&0&1&0&1&0&0&1&0&0\\ 0&0&0&1&0&0&c&0&0&0\\ 0&1&1&0&0&0&0&0&1&1\\ 0&0&0&0&b&0&0&1&0&1\\ 0&0&0&1&0&0&1&0&1&0\\ 0&0&1&0&0&1&0&1&0&1\\ 0&0&0&0&0&1&1&0&1&0\\ \end{pmatrix}$$
a) Déterminer les entiers $a$, $b$ et $c$ pour que la matrice $M$ représente la matrice d'adjacence associée au graphe $\Gamma$, les sommets étant pris dans l'ordre alphabétique.
Soit $S$ la matrice définie par : $S=M+M^{2}+M^{3}.$
On admet que :
$$M^{3}=\begin{pmatrix}\\ 4&7&8&7&1&4&2&2&5&3\\ 7&4&9&3&2&8&1&4&4&3\\ 8&9&8&10&1&10&5&2&11&3\\ 7&3&10&2&6&5&0&8&2&5\\ 1&2&1&6&0&2&5&0&4&0\\ 4&8&10&5&2&6&2&4&8&7\\ 2&1&5&0&5&2&0&7&1&6\\ 2&4&2&8&0&4&7&0&8&1\\ 5&4&11&2&4&8&1&8&4&8\\ 3&3&3&5&0&7&6&1&8&2\\ \end{pmatrix}$$
$$\text{et }S=\begin{pmatrix}7&9&11&9&2&6&2&3&6&3\\ 9&7&12&5&2&10&1&4&6&4\\ 11&12&13&12&2&13&5&4&13&5\\ 9&5&12&6&7&6&2&9&4&5\\ 2&2&2&7&2&2&6&2&4&1\\ 6&10&13&6&2&10&3&5&11&9\\ 2&1&5&2&6&3&3&8&3&7\\ 3&4&4&9&2&5&8&3&9&3\\ 6&6&13&4&4&11&3&9&8&10\\ 3&4&5&5&1&9&7&3&10&5\\ \end{pmatrix}$$
b) Déterminer, en justifiant, le nombre de chemins de longueur $3$ reliant $F$ à $L.$
Préciser ces chemins.
c) Déterminer, en justifiant, le nombre de chemins de longueur $3$ partant de $E.$
d) Que signifie le coefficient à l'intersection de la première ligne et de la troisième colonne de $S$ ?
4) Un défilé part tous les jours à $14$ h du sommet $N.$
Louisa et Antoine choisissent de déjeuner dans un restaurant situé au sommet $E$ avant d'aller admirer le défilé.
a) À l'aide d'un algorithme, déterminer le chemin que doivent emprunter Louisa et Antoine pour se rendre du restaurant au départ du défilé le plus rapidement.
b) À quelle heure au plus tard doivent-ils quitter le restaurant pour assister au début du défilé ?

Ajouter un commentaire