Bac Physique chimie 1er groupe S2, S2A, S4, S5 2020
Exercice 1 (4 points)
L'éthanoate d'éthyle est un ester qui peut être utilisé comme solvant.
A la date $t=0\;s$, il effectue un mélange équimolaire d'ester et d'hydroxyde de sodium, de volume $V=1\;L$,contenant $n_{\text{ester}}=5.10^{-2}\;mol\ $ et $\ n_{\text{soude}}=5.10^{-2}\;mol.$
Le mélange est maintenu à une température constante.
Toutes les quatre minutes, le groupe d'élèves prélève $5\;mL$ du mélange qu'il dilue avant de doser l'hydroxyde de sodium restant par une solution d'acide chlorhydrique de concentration molaire $Ca=10^{-2}\;mol/L.$
On désigne par $V_{a}$ le volume d'acide versé.
Les résultats sont consignés dans le tableau suivant :
$$\begin{array}{|c|c|c|c|c|c|c|c|c|c|c|c|c|}
\hline
t(min)&0&4&8&12&16&20&24&28&32&36&40&44\\
\hline
V_{a}(mL)&25.0&22.0&19.8&18.0&16.5&15.0&13.8&12.8&12.0&11.5&11.0&10.5\\ \hline
[\text{ester}]\text{ en }mol.L^{-1}&&&&&&&&&&&&\\
\hline
\end{array}$$
1.1. Définirlasaponification et rappelerses caractéristiques. (0.5 point)
1.2. Quel est l’intérêt de la dilutionavant le dosage ? (0.25 point)
1.3. L’équation bilan complète de la réaction de saponification s’écrit :
$CH_{3}-COO-C_{2}H_{5}+(Na^{+}+ OH^{-})\rightarrow {(CH_{3}-COO^{-}+ Na^{+}) +C_{2}H_{5}OH}$
1.3.1. Montrer que la concentration de l'ester contenu dans chaque prélèvement est donnée parla relation : $[\text{ester}]=\dfrac{0.01.V_{a}}{5}$ en $mol/L$ avec $V_{a}$ en $mL.$ (0.5 point)
1.3.2. Recopier le tableau ci-dessus et le compléter en calculantla concentration de l’esterpour chaque prélèvement. (0.5 point)
1.3.3 Tracer la courbe représentative de la concentration de l’ester en fonction du temps : $[\text{ester}]=f(t).$ (0.7 5point)
Echelles : $1\;cm$ pour $4\;min$ ; $1\;cm$ pour $0.5\cdot10^{-2}\;mol\cdot L^{-1}$
1.4. Le groupe d'élèves s'intéresse à la vitesse de la réaction.
1.4.1 Déterminer graphiquement la vitesse moyenne de disparition de l'ester entre les instants $t_{1}=10\;min$ et $t_{2}=30\;min$. (0.5 point)
1.4.2. Donner la relation définissant la vitesse instantanée de disparition de l'ester.
Déterminer graphiquement la valeur de cette vitesse à $t_{0}=0\;min$ et à $t_{3}=20\;min.$
Dans quel sens évolue la vitesse instantanée ?
Justifier cette évolution.
Exercice 2 (4 points)
Elle permet une récupération plus rapide après un effort physique intense puisqu'elle est assimilée et distribuée aux muscles.
Elle se retrouve dans le lait, le fromage de chèvre ... et est parfois consommée associée à la leucine ou à l'isoleucine afin d'augmenter la masse musculaire.
La formule semi-développée de la valine est :
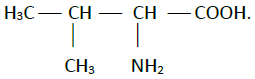 .
.
2.1. La molécule de valine est-elle chirale ?
Justifier. (0.5 point)
2.2. Donner la représentation de Fischer des deux énantiomères de la valine et les nommer. (0.5 point)
2.3. On effectue la dé carboxylation de la molécule de valine ; il se forme du dioxyde de carbone et un composé organique $A$.
2.3.1. Écrire l'équation bilan de la réaction de décarboxylation. (0.5 point)
2.3.2. Préciser la fonction chimique du composé organique $A$ ainsi que sa classe. (0.5 point)
2.4. On fait réagir la valine avec le composé $A$ pour obtenir un composé organique $B.$
2.4.1. Écrire l'équation bilan de la réaction entre la valine et le composé $A.$ (0.5 point)
2.4.2. Nommer le composé $B.$ (0.5 point)
2.5. On désire synthétiser, à partir de la valine,le dipeptide suivant :
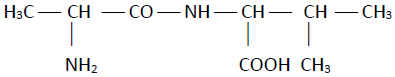
2.5.1. Écrire la formule et donner le nom systématique de l'autre acide $\alpha-\text{aminé}.$ (0.5 point)
2.5.2. Écrire l'équation bilan de la réaction de synthèse de ce dipeptide à partir des deux acides $\alpha-\text{aminés}.$ (0.5 point)
N.B :
Exercice 3 (4 points)
Le vol d'une navette spatiale comprend trois étapes : le lancement, le vol orbital et l'atterrissage.
On se propose d'étudier le vol orbital.
Dix minutes après le décollage, la navette est en mouvement circulaire uniforme autour de la terre à l'altitude $h$.
Sa masse est $m=69.68\cdot10^{3}\;kg.$
L'intensité du champ de gravitation terrestre à l'altitude $h$ est $G_{h}=6.95\;m\cdot s^{-2}.$
Le rayon de la terre est $R_{T}=6380\;km.$
La masse de la terre sera notée $M_{T}.$
3.1. Rappeler l'expression de la force de gravitation universelle, puis établir l'expression de l'intensité du champ de gravitation $G_{h}$ en fonction de $G_{o}\;,\ R_{T}$ et $h\ ;\ G_{o}$ étant l'intensité du champ de gravitation au sol $(G_{o}=9.80\;m\cdot s^{-}2).$ (0.5 point)
3.2. En déduire l'expression de l'altitude $h$ dela navette.
Calculer sa valeur. (0.5 point)
3.3. Etablir l'expression de la vitesse $V$ du centre d'inertie de la navette à l'altitudehen fonction de $G_{h}\;,\ R_{T}\ $ et $\ h.$
Calculer cettevitesse $V$ pour $h=1196\;km.$ (0.75 point)
3.4. Etablir l'expression de la période $T$ de révolutionde la navette à l'altitude hen fonction de $R_{T}\;,\ V\ $ et $\ h.$
Calculer la période $T.$ (0.5 point)
3.5. La navettese trouvant à l’altitude $h$, se déplace d’Ouest en Est.
Calculer l'intervalle de temps $\Delta\,t$ qui sépare deux passages successifs de la navette à la verticale d’un point de la Terre.
On rappelle que la période de révolution de la Terre autour de l’axe des pôles est $T_{T}=86\,164\;s.$ (0.75 point)
3.6. La navette doit être mise surl’orbite d’altitude $h'=2h$ pour une autre mission avant son retour.
3.6.1. Donner l’expression de l’énergie mécanique de la navette évoluant à l’altitude hen fonction de $G_{o}\;,\ R_{T}\;,\ m\ $ et $\ h.$
L’expression de l’énergie potentielle de gravitation du satellite est ; $E_{p}(r)=-\dfrac{KM_{T}m}{r}$ avec $r$ le rayon de l’orbite de la navette. (0.5 point)
3.6.2. Déterminerl’énergie que doivent fournir les moteurs pourfaire passer la navette del’altitude $h$ à l’altitude $h'=2h.$ (0.5 point)
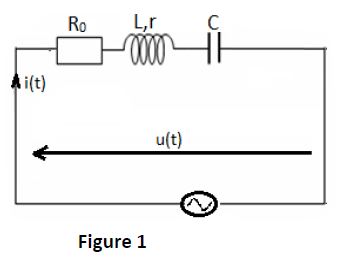
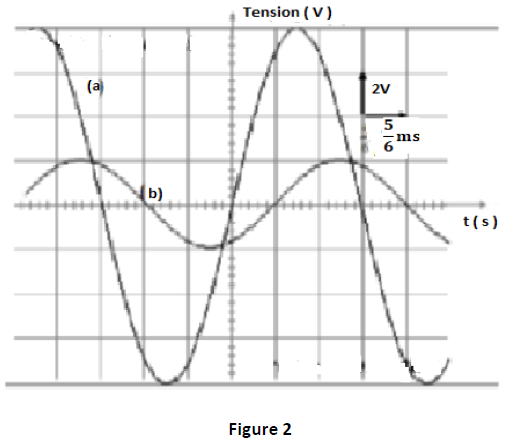
Exercice 4 (4 points)

Commentaires
Awa Ndiaye (non vérifié)
jeu, 05/29/2025 - 22:42
Permalien
Je veux réussir au
Ajouter un commentaire