Bac maths, S1 Gabon août 2020
Exercice 1 (5 points)
Question à choix multiples
Pour chacune des questions, une seul des quatre propositions est exacte.
Vous indiquerez sur votre copie le numéro de la question et la lettre correspondant à la réponse choisie.
Exemple :
question 1.a Réponse A et 1.b Réponse C.
Une bonne réponse rapporte 1 pt (0.5 pt+0.5 pt), une mauvaise réponse fait perdre 0.25 point, l'absence de réponse ne donne droit à aucun point et n'en fait perdre aucun ; si le total des points est négatif, la note à cet exercice est ramenée à zéro.
1. On note $(\mathcal{C})$ la courbe représentative dans un repère orthonormal de la fonction $f$ définie sur $K=[1\ ;\ +\infty[$ par :
$$f(x)=\dfrac{x^{2}+x\ln x}{x+1}$$
$$f(x)=\dfrac{x^{2}+x\ln x}{x+1}$$
a. laquelle des affirmations suivantes est correcte ?
$$\begin{array}{|c|c|c|c|} \hline \text{Réponse A}&\text{Réponse B}\\ \hline (\mathcal{C})\text{ admet une}&(\mathcal{C})\text{ admet une}\\\text{asymptode oblique}&\text{branche parabolique}\\\hline\text{Réponse C}&\text{Réponse D}\\\hline (\mathcal{C})\text{ admet une}&(\mathcal{C})\text{ admet une}\\ \text{asymptote vertical}&\text{asymptode horizontale}\\\hline \end{array}$$
b. Laquelle des affirmations suivantes est correcte ?
$$\begin{array}{|c|c|c|c|} \hline \text{Réponse A}&\text{Réponse B}&\text{Réponse C}&\text{Réponse D}\\ \hline f\text{ est strictement}& &f\text{ n'est pas}&f\text{ est strictement}\\ \text{décroissante sur }K&f\text{ est constant }k&\text{strictement monotone}&\text{croissante sur }K\\& &\text{sur }k&\\\hline \end{array}$$
2. Soient $A(1\ ;\ -1\ ;\ 0)$, $B(3\ ;\ 0\ ;\ 1)$, $C(1\ ;\ 2\ ;\ -1)$, $D(1\ ;\ 0\ ;\ 0)$ quatre points de l'espace muni d'un repère orthonormé direct $\left(O\;,\ \vec{i}\;,\ \vec{j}\;,\ \vec{k}\right)$ alors :
a. $\left|(\overrightarrow{AB}\wedge\overrightarrow{AC})\cdot\overrightarrow{AD}\right|$ est égal à :
$$\begin{array}{|l|l|l|l|} \hline \text{Réponse A}&\text{Réponse B}&\text{Réponse C}&\text{Réponse D}\\ \hline 2&5&\dfrac{1}{3}&\dfrac{5}{2} \\\hline \end{array}$$
b. Une équation cartésienne du plan $(ABC)$ est :
$$\begin{array}{|l|l|l|l|} \hline \text{Réponse A}&\text{Réponse B}&\text{Réponse C}&\text{Réponse D}\\ \hline 2x-y-3z-3=0&2x+y+3z-3=0&2x-y-3z+3=0&\text{Aucune des}\\ & & &\text{réponses n'est juste} \\\hline \end{array}$$
3. Soit $z$ un nombre complexe non nul d'argument $\theta.$
On pose : $Z=\dfrac{-\mathrm{i}+\sqrt{3}}{2}\overline{Z}$
a. Un argument de $Z$ est alors :
$$\begin{array}{|l|l|l|l|} \hline \text{Réponse A}&\text{Réponse B}&\text{Réponse C}&\text{Réponse D}\\ \hline -\dfrac{\pi}{6}+\theta&-\dfrac{\pi}{6}-\theta&\dfrac{\pi}{6}-\theta&\dfrac{\pi}{6}+\theta\\ \hline \end{array}$$
b. Le conjugué de $Z$ est alors :
$$\begin{array}{|l|l|l|l|} \hline \text{Réponse A}&\text{Réponse B}&\text{Réponse C}&\text{Réponse D}\\ \hline \overline{Z}=\left(\dfrac{-\mathrm{i}-\sqrt{3}}{2}\right)\overline{Z}&\overline{Z}=\left(\dfrac{\mathrm{i}-\sqrt{3}}{2}\right)Z&\overline{Z}=\left(\dfrac{\mathrm{i}+\sqrt{3}}{2}\right)Z&\overline{Z}=\left(\dfrac{\mathrm{i}-\sqrt{3}}{2}\right)\overline{Z}\\ \hline \end{array}$$
4. La courbe ci-dessous est la courbe $(\mathcal{C})$ représentative d'une fonction $f$ dérivable sur $I$
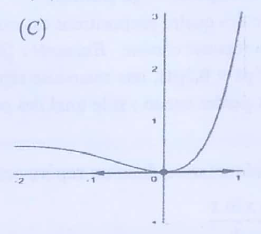
a. Laquelle des quatre courbes ci-dessous représente une primitive $F$ de la fonction $f$ sur $I$ :
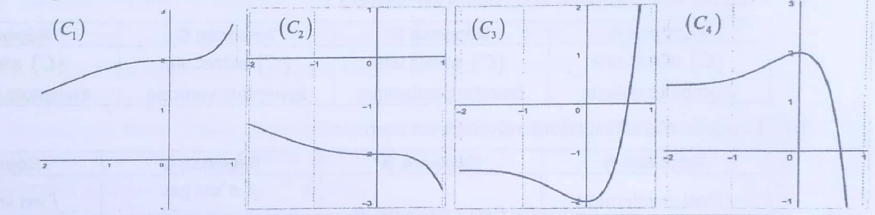
$$\begin{array}{|l|l|l|l|} \hline \text{Réponse A}&\text{Réponse B}&\text{Réponse C}&\text{Réponse D}\\ \hline (\mathcal{C}_{3})&(\mathcal{C}_{4})&(\mathcal{C}_{2})&(\mathcal{C}_{1})\\ \hline \end{array}$$
b. Laquelle des affirmations suivantes est correcte
$$\begin{array}{|l|l|l|l|} \hline \text{Réponse A}&\text{Réponse B}&\text{Réponse C}&\text{Réponse D}\\ \hline F'(0)=1&F'(0)=0&F'(0)=-2&F'(0)=2\\ \hline \end{array}$$
5. On désigne par $A$ et $B$ deux événements d'un univers muni d'une probabilité $p.$
On sait que $p(A\cup B)=\dfrac{7}{8}\text{ et }p(\overline{B})=\dfrac{5}{8}.$
a. Si $A$ et $B$ sont indépendant alors la probabilité de l'événement $A$ est égale à :
$$\begin{array}{|l|l|l|l|} \hline \text{Réponse A}&\text{Réponse B}&\text{Réponse C}&\text{Réponse D}\\ \hline \dfrac{5}{8}&\dfrac{1}{8}&\dfrac{1}{2}&\text{Aucune des}\\ & & &\text{réponses n'est juste} \\ \hline \end{array}$$
a. Si $A$ et $B$ sont incompatible alors la probabilité de l'événement $A$ est égale à :
$$\begin{array}{|l|l|l|l|} \hline \text{Réponse A}&\text{Réponse B}&\text{Réponse C}&\text{Réponse D}\\ \hline \dfrac{5}{8}&\dfrac{1}{8}&\dfrac{1}{2}&\text{Aucune des}\\ & & &\text{réponses n'est juste} \\ \hline \end{array}$$
Exercice 2 Arithmétique - Congruences et critères de divisibilité 3 points
1 on considère l'équation $(E)\ :\ 5x+3y=16$ où $x$ et $y$ sont des entiers naturels.
a. Justifier que l'équation $5x+3y=1$ admet au moins une solution
b. Déterminer une solution de l'équation $5x+3y=1$, en déduire une solution particulière de $(E).$
c. Résoudre alors $\mathbb{N}^{2}$ l'équation $(E).$
2. ELLA Paul est un candidat de terminale C, il a passé les épreuves du second tour en mathématiques (Coefficient 5) et en philosophie ( coefficient 3).
Il a obtenu la note de 08/20 dans les deux disciplines au premiers tour.
Pour être déclaré admis au second tour (avoir 10/20), il lui faut rattraper 16 points.
On désigne par $8+x$ sa note à l'oral de mathématiques et $8+y$ celle obtenue à l'oral de philosophie où $x$ et $y$ sont des entiers naturels.
A l'aide de la question précédente, déterminer toutes les notes possibles d'ELLA Paul en mathématiques et en philosophie pour qu'il obtiennent exactement $10/20$ au second tour.
Exercice 3 Similitude directes du plan 3 points
On considère dans le plan orienté un triangle rectangle $ABC$ tel que :
$$Ab=2AC\quad\text{ et }\quad(\overrightarrow{AB}\;,\ \overrightarrow{AC})=\dfrac{\pi}{2}\quad[2\pi]$$
On désigne par $I$ le milieu de $[AB]$ et $J$ un point tel que $A$ soit milieu de $[CJ].$
1. Faire une figure soignée que l'on complétera au fur et à mesure.
2. a. Justifier qu'il existe une unique similitude directe $S$ du plan qui transforme $I$ en $C$ et $A$ en $J.$
b. Déterminer le rapport et l'angle de la similitude $S$
3. Considérons les cercles $(\mathcal{C}_{1})$ et $(\mathcal{C}_{2})$ respectivement de diamètre $[IC]$ et $[AJ]$
a. Montrer que le cercle $\Omega$ de $S$ appartient à $(\mathcal{C}_{1})\cap(\mathcal{C}_{2})$
b. Déterminer et construire alors $\Omega.$
4. La droite $(\Delta_{1})$ est la tangente à $(\mathcal{C}_{1})$ au point $C$, la droite $(\Delta_{2})$ est la tangente à $(\mathcal{C}_{2})$ au point $J.$
a. Démontrer que $S(\mathcal{C})=K$ où $K$ est le point d'intersection de $(\Delta_{1})$ et $(\Delta_{2})$
b. Place le point $L$, image de $B$ par $S$, on expliquera la construction.
Exercice 4 Étude d'une suite numérique 5 point
L'objectif de cet exercice est d'étudier une suite $(x_{n})$ dont les termes sont définis comme les solutions d'équations $f_{n}(x)=0$, où $f_{n}$ est une famille de fonctions définies pour tout entier naturel $n.$
Partie A
Soit $g$ la fonction définie sur $[1\ ;\ +\infty[$ par $g(x)=x-\ln x.$
1. Justifier que la fonction $g$ est strictement croissante sur $[1\ ;\ +\infty[.$
2. a. En utilisant $g(1)$, justifier clairement le signe de $g(x)$ pour $x$ élément de $[1\ ;\ +\infty[.$
b. En déduire que pour tout entier naturel $n\geq 1\;,\ \sqrt{n}\geq\ln\sqrt{n}.$
Partie B
Pour tout entier naturel $n$, on considère la fonction $f_{n}$ définie sur $]1\ ;\ +\infty[$ par :
$$f_{n}(x)=n(x-1)+\ln(x-1)$$
$$f_{n}(x)=n(x-1)+\ln(x-1)$$
On note $f'_{n}$ la fonction dérivée de la fonction $f_{n}.$
1. a. Calculer $f'_{n}(x)$ puis justifier que $f_{n}$ est strictement croissante sur $]1\ ;\ +\infty[$
b. Calculer les limites de $f_{n}$ en $+\infty$ et en $1.$
c. En déduire que, pour tout entier naturel $n$, l'équation $f_{n}(x)=0$ admet une solution $x_{n}$ dans l'intervalle $]1\ ;\ +\infty[$
2. Justifier que $x_{0}=2.$
3. Soit $n$ un entier naturel.
a. Montrer que pour tout $x$ appartenant à $]1\ ;\ +\infty[$ on a :
$$f_{n+1}(x)-f_{n}(x)=x-1\;,$$ puis que :
$$f_{n+1}(x)>f_{n}(x)$$
b. En déduire que $f_{n+1}(x_{n})>0.$
c. En utilisant le sens de variation de $f_{n+1}$, montrer que la suite $(x_{n})$ est décroissante.
En déduire que la suite $(x_{n})$ converge.
4. a. En utilisant la question 2. b. de la partie A, démontrer que pour tout entier naturel $n\geq 1$
$$f_{n}\left(1+\dfrac{1}{\sqrt{n}}\right)>0$$
$$f_{n}\left(1+\dfrac{1}{\sqrt{n}}\right)>0$$
b. En déduire que pour tout entier naturel $n\geq 1$
$$1<x_{n}\leq 1+\dfrac{1}{\sqrt{n}}$$
$$1<x_{n}\leq 1+\dfrac{1}{\sqrt{n}}$$
c. Démontrer la limite de la suite $(x_{n}).$
Exercice 5 Intégrale et suites numériques 4 points
1. Soit $f$ la fonction définie sur $\mathbb{R}$ par :
$$f(x)=x^{2}\mathrm{e}^{1-x}.$$
On désigne par $(\mathcal{C})$ sa courbe représentative dans un repère orthonormé $(O\;,\ \vec{i}\;,\ \vec{j})$ d'unité graphique $2\,cm.$
a. Déterminer les limites de $f$ en $-\infty$ et en $+\infty.$
En déduire une conséquence graphique pour la courbe $(\mathcal{C})$ dans le cas de la limite de $f$ en $+\infty$
b. Justifier que $f$ est dérivable sur $\mathbb{R}$ et déterminer sa fonction dérivée $f'.$
c. Dresser le tableau de variation de $f$ et tracer la courbe $(\mathcal{C}).$
2. Soit $n$ un entier naturel non nul.
On considère l'intégrale $I_{n}$ définie par : $$I_{n}=\int_{0}^{1}x^{n}\mathrm{e}^{1-x}\mathrm{d}x.$$
a. A l'aide d'une intégration par partie, établir une relation entre $I_{n+1}$ et $I_{n}.$
b. Calculer $I_{1}$ et $I_{2}.$
c. Donner une intégration graphique de $I_{2}.$
On fera apparaitre sur le graphique de la question 1. c.
3. a. Démontrer que pour tout nombre réel $x$ de l'intervalle $[0\ ;\ 1]$ et pour tout entier naturel non nul $n$, on a l'inégalité suivante :
$$x^{n}\leq x^{n}\mathrm{e}^{1-x}\leq x^{n}\mathrm{e}$$
b. En déduire un encadrement de $I_{n}$ puis la limite de $I_{n}$ quand $n$ tend vers $+\infty.$

Ajouter un commentaire