Douane - Épreuve de Mathématiques - 2013
Exercice 1 (5 points)
Dans le plan muni d'un repère orthonormal $(O\;,\ I\;,\ J)$ on donne les points
$$A\begin{pmatrix} 1\\2\end{pmatrix}\ \text{ et }\ B\begin{pmatrix} -1\\-1\end{pmatrix}$$
$f$ est l'application affine dont la représentation graphique est la droite $(AB).$
1) Détermine l'expression littérale de cette application affine. $\quad(1.5\,\text{pts})$
2) Calcule $f(0)\ $ et $\ f(-2)\quad(2\,\text{pts})$
3) On considère l'inéquation à deux inconnues :
$$2x-y+1>0$$
Indique parmi les couples suivants :
$$(0\;;\ 0)\;,\ \left(-\dfrac{3}{2}\;;\ 1\right)\;,\ (-0.2\;;\ -1)\;,\ (\sqrt{3}\;;\ -1)\ \text{ et }\ (1\;;\ 1)$$
ceux qui sont solutions de cette inéquation. $\quad(1.5\,\text{pts})$
Exercice 2 (4 points)
On donne les réels suivants :
$$a=\sqrt{3}-2\ \text{ et }\ b=3\sqrt{3}-5\ \text{ et }\ E=\dfrac{\sqrt{52-30\sqrt{3}}}{7-4\sqrt{3}}$$
1) Détermine le signe de $a$ et celui de $b\quad(2\,\text{pts})$
2) Calcule $a^{2}\ $ et $\ b^{2}\quad(1\,\text{pt})$
3) Démontre que $E=\sqrt{3}-1\quad(1\,\text{pt})$
Exercice 3 (6 points)
Dans le plan muni d'un repère orthonormal $(O\;,\ I\;,\ J)$ on donne les points :
$$A\begin{pmatrix} 5\\0\end{pmatrix}\;,\ B\begin{pmatrix} 6\\2\end{pmatrix}\ \text{ et }\ C\begin{pmatrix} 2\\4\end{pmatrix}$$
1) Justifie que le triangle $ABC$ est rectangle en $B.\quad(1\,\text{pt})$
2) Construis le point $D$ tel que $\overrightarrow{BD}=\overrightarrow{AB}$ puis calcule ses coordonnées.$\quad(1.5\,\text{pts})$
3) Construis le point $E$, symétrique de $C$ par rapport à $B$ puis calcule ses coordonnées.$\quad(1.5\,\text{pts})$
4) Quelle est la nature du quadrilatère $ACDE\ ?\quad(1.5\,\text{pts})$
5) Soit $F\begin{pmatrix} 12\\4\end{pmatrix}$, justifie que $F$ est l'image de $E$ par la translation de vecteur $\overrightarrow{AD}\quad(0.5\,\text{pt})$
Exercice 4 (5 points)
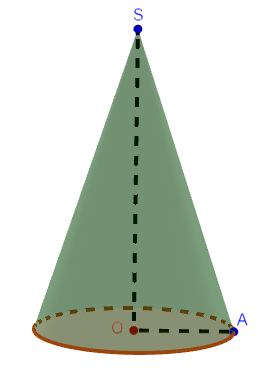
Le schéma ci-dessous représente un cône de révolution de sommet $S$ et dont la base est un disque de centre $O$ et de rayon $OA=3\,cm.$
1) Sachant que l'angle $\widehat{OSA}=30^{\circ}$, calcule la génératrice $SA$ de ce cône et montre que $SO=3\sqrt{3}\quad(2\,\text{pts})$
2) Montre que le volume de ce cône de révolution est $9\pi\sqrt{3}\;cm^{3}\quad(1.5\,\text{pts})$
3) On coupe ce cône par un plan parallèle à sa base de telle sorte que la base du cône réduit qui en résulte ait une aire de $\dfrac{9\pi}{4}\;cm^{2}.$
Calcule le coefficient de réduction $k.\quad(1.5\,\text{pts})$
$$\text{Durée 2 heures}$$

Ajouter un commentaire