ENSA - Épreuve de Sciences Physiques - 2018

Les esters jouent un rôle important dans la chimie des parfums et dans l'industrie alimentaire car ils possèdent une odeur florale ou fruitée. La transpiration de l'être humain contribue à la disparition de l'odeur du parfum.

 

1) Écrire, à l'aide de formules générales, l'équation-bilan de la réaction d'hydrolyse d'un ester. Justifier alors brièvement l'altération de l'odeur du parfum par la sueur.$\quad(1\,\text{pt})$

 

2) Au laboratoire on étudie l'hydrolyse d'un ester. Une méthode de contrôle de la réaction consiste à mesurer le $\text{pH}$ du milieu réactionnel à intervalles de temps réguliers. Dire comment évolue le $\text{pH}$ du milieu réactionnel en fonction du temps.$\quad(1\,\text{pt})$

 

3) A une date $t$ donnée, la mesure du $\text{pH}$ donne $\text{pH}=2.6$ et à cette date la concentration molaire volumique de l'acide formé est $C_{A}= 6.25\cdot 10^{-3}\,mol.L^{-1}.$

 

L'acide sera noté $AH$ et sa base conjuguée $A^{-}.$

 

Montrer que l'expression du $\text{pK}_{a}$ du couple acide-base associé à cet acide est donnée par la relation :

$$\text{pK}_{a}=2\text{pH}+\log(C_{A}- 10^{-\text{pH}})\qquad(1.5\,\text{pts})$$

En déduire la valeur du $\text{pK}_{a}.\quad(0.5\,\text{pt})$

 

4) L'acide AH est dérivé d'un acide carboxylique $RCOOH$ par remplacement d'un atome d'hydrogène du groupe alkyle $R$ par un atome de chlore.

 

a) Sachant que la masse molaire moléculaire de l'acide vaut : $M=108.5\,g.mol^{-1}$ déterminer sa formule brute.$\quad(1.5\,\text{pts})$

 

Écrire sa formule semi développée.$\quad(0.5\,\text{pt})$

 

b) La molécule de l'acide possède un carbone asymétrique ;

 

Représenter alors les configurations des deux énantiomères de l'acide.$\quad(1\,\text{pt})$

 

On donne :

 

$M(H)=1\,g.mol^{-1}\;;\ M(C)=12\,g.mol^{-1}\;;\ M(O)=16\,g.mol^{-1}\;;\ M(Cl)=35.5\,g.mol^{-1}$

Partie A

 

L'isotope 4 de l'Hélium est représenté par le symbole : $_{2}^{4}He.$

 

1) Qu'appelle-t-on nucléides isotopes ?$\quad(0.5\,\text{pt})$

 

2) Donner la composition de l'isotope 4 de l'Hélium.$\quad(0.5\,\text{pt})$

 

3) Quelle est, en MeV/nucléon, l'énergie de liaison par nucléon de ce nucléide ?$\quad(0.5\,\text{pt})$

 

On donne :

 

$-\ $ Célérité de la lumière : $c=3\cdot 10^{8}\,m.s^{-1}$, et

 

$-\ $ Les masses : $m\left(_{2}^{4}He\right)=4.00260\,u\;;\ m_{p}=1.00728\,u\;;\ m_{n}=1.00867\;u\;;\ 1\,u=1.67\cdot 10^{-27}\,kg.$

 

Partie B

 

La fission d'un noyau d'Uranium $235$ produit un isotope du Strontium et un isotope du Xénon selon l'équation :

$$_{0}^{1}n+_{\ 92}^{235}U\ \longrightarrow\ _{\ x}^{94}Sr+_{54}^{\ y}Xe+2_{0}^{1}n$$

1) En utilisant les lois de conservations habituelles, calculer $x\ $ et $\ y.\quad(0.5\,\text{pt})$

 

2) Dans certains réacteurs dits surgénérateurs, il y a possibilité de capture d'un neutron par un noyau $_{\ 92}^{235}U.$

 

Quel est l'isotope de l'uranium obtenu ?$\quad(0.5\,\text{pt})$

 

3) Cet isotope, radioactif, subit une transmutation $\beta^{-1}$ pour donner un isotope du Neptunium $(N_{p})$, lui-même radioactif et qui par une nouvelle désintégration $\beta^{-1}$ donne l'isotope $_{\ 94}^{239}Pu$ du Plutonium.

 

Écrire les deux équations correspondant aux deux transmutations envisagées en utilisant les symboles convenables.$\quad(1\,\text{pt})$

 

Une fission libère d'autres neutrons dits rapides, ayant une vitesse $V_{0}=20\,000\;km.s^{-1}.$ Pour qu'un neutron puisse provoquer une nouvelle fission, il doit avoir une vitesse $V_{1}=2\;km.s^{-1}.$ Le ralentissement des neutrons se fait par chocs successifs avec les noyaux atomiques d'un modérateur. Un neutron de vitesse $V_{0}=20\,000\;km.s^{-1}$ heurte un noyau de deutérium $_{1}^{2}H$ initialement au repos. On suppose que le choc est parfaitement élastique et que les vitesses des particules après le choc ont même direction que la vitesse du neutron incident.

 

4) En appliquant les lois de la mécanique classique, calculer la vitesse du neutron après le choc$\quad(0.5\,\text{pt})$

 

5) Combien de chocs identiques seraient nécessaires pour que la vitesse du neutron soit égale à $2\;km.s^{-1}.\quad(0.5\,\text{pt})$

 

Pour cette question on prendra : Masse du neutron=$1\,u$ ; masse du noyau de $_{1}^{2}H=2\,u.$

 

Partie C

 

Un des déchets radioactifs est le Plutonium $239.$ A un instant pris comme origine des temps, on envisage un échantillon contenant $N_{0}$ noyaux de plutonium.

 

1) Donner, en fonction de $N_{0}\;,\ \lambda\ $ et $\ t$, l'expression du nombre $N(t)$ de noyaux restant dans l'échantillon à la date $t.\quad(0.5\,\text{pt})$

 

2) Quelle est en, années, la demi-vie du Plutonium ?$\quad(0.75\,\text{pt})$

 

3) Quelle est, en fonction de $N_{0}\ $ et $\ \lambda$, l'expression de l'activité initiale $A_{0}$ de l'échantillon ?$\quad(0.5\,\text{pt})$

 

4) Au bout de combien de temps cette activité aura-t-elle diminué de $90\%\ ?\quad(0.5\,\text{pt})$

 

Données :

 

$\lambda$ (constante radioactive du Plutonium) $=0.92\cdot 10^{-12}\, s^{-1}$ ; Une année$=3.1\cdot 10^{7}\,s$

On réalise une figure d'interférences lumineuses à l'aide d'une source principale $F$ et de fentes fines $F_{1}\ $ et $\ F_{2}.$ La distance $F_{1}F_{2}=a.$ Un écran $E$ est placé parallèlement aux fentes à une distance $D$ de celles-ci.

 

 

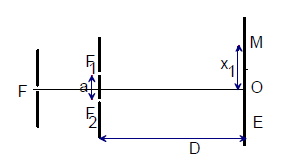
A) La source principale $F$ émet une lumière monochromatique de longueur d'onde $\lambda.$

 

1) Les fentes $F_{1}\ $ et $\ F_{2}$ sont-elles des sources cohérentes ? Justifier brièvement la réponse.

 

2) Qu'observe-t-on alors sur l'écran $E\ ?$ Quel caractère de la lumière met-on ainsi en évidence ?

 

3) Exprimer la différence de marche $\delta$ des rayons lumineux se superposant au point $M$ d'abscisse $x$ sur l'écran $E.$ Calculer $\delta$ pour $x= x_{1}.$

 

4) Définir puis calculer l'interfrange $i.$

 

5) Qu'appelle-t-on ordre d'interférence ? A quelle distance du point $O$ on trouve alors la frange noire d'ordre $11\ ?$

 

B) La source $F$ émet maintenant une lumière constituée de radiations de longueurs d'onde $\lambda_{1}\ $ et $\ \lambda_{2}.$

 

1) Calculer les interfranges $i_{1}\ $ et $\ i_{2}$ correspondant respectivement aux radiations de longueurs d'ondes $\lambda_{1}\ $ et $\ \lambda_{2}.$

 

2) Déduire des résultats précédents l'aspect de la frange centrale ainsi que celui de sa voisine immédiate.

 

C) On éclaire cette fois-ci les fentes $F_{1}\ $ et $\ F_{2}$ à l'aide d'une lumière blanche issue de la fente principale $F.$

 

1) Dans quelle région du spectre électromagnétique se situe la lumière blanche ? Cette lumière est-elle monochromatique ? Justifier.

 

2) Quelle est la couleur de la frange centrale ? Quel est l'aspect observé au voisinage immédiat de la frange centrale ?

 

3) Quelles sont les radiations éteintes en un point $M'$ situé à la distance $x_{2}$ du point $O\ ?$ Quel est alors à cet endroit, l'aspect de l'écran ?

 

Données :

 

$D=3.0\,m\;;\ a=1.0\,mm\;;\ x_{1}=2.0\,cm\;;\ x_{2}=3.0\,cm\;;\ \lambda=680\,nm$

 

$\lambda_{1}=700\,nm$ (radiation rouge) ; $\lambda_{2}=500\,nm$ (radiation bleue) ; longueurs d'onde dans la région visible du spectre électromagnétique :

$$400\,nm\leq\lambda\leq 750\,nm$$

 

$$\text{Durée 2 heures}$$