ENSA - Épreuve de Sciences Physiques - 2019

Données : $M(H)=1\,g.mol^{-1}\;;\ M(C)=12\,g.mol^{-1}\;;\ M(O)=16\,g.mol^{-1}$

 

Un des composants du vin est l'acide malique $COOH-CH_{2}-CHOH-COOH$ ou acide 2-hydroxybutanedioique.

 

Lors de la fermentation du vin l'acide malique se décompose en donnant du dioxyde de carbone de l'acide lactique ou acide 2-hydroxypropanoïque

 

1) Écrire l'équation de la réaction de fermentation de l'acide malique en entourant les groupes fonctionnels de l'acide obtenu puis les nommer.$\quad(1.5\,\text{pts})$

 

2) Pourquoi la molécule d'acide lactique est chirale ? Donner la représentation de Fischer des deux énantiomères.$\quad(1\,\text{pt})$

 

3) On réalise un suivi cinétique par dosage, l'évolution de la concentration massique $C_{m}(t)$ en fonction du temps de l'acide malique dans un vin de volume constant. Les résultats obtenus ont permis de tracer la courbe $C_{m}=f(t)$ ci-contre.

 

 

 

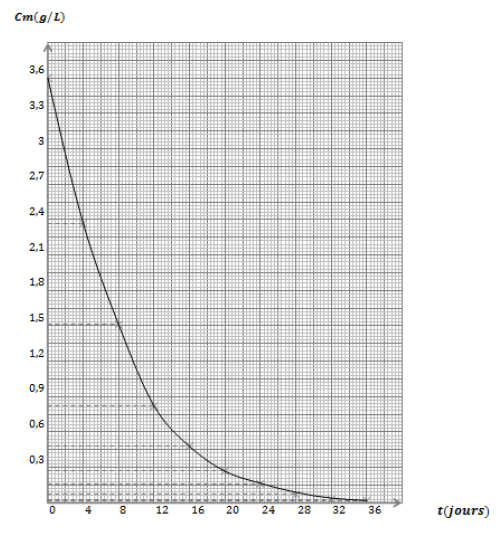
3.1) Exprimer la concentration molaire $C$ de l'acide malique en fonction de la concentration massique $C_{m}.\quad(0.5\,\text{pt})$

 

3.2) Définir la vitesse volumique de disparition de l'acide malique. L'exprimer en fonction de la concentration massique.$\quad(1\,\text{pt})$

 

3.3) Déterminer la date à laquelle la concentration molaire de l'acide lactique vaut $C'=2.01\cdot 10^{-2}\,mol.L^{-1}\quad(1.5\,\text{pts})$

 

3.4) Déterminer à cette date la vitesse volumique de disparition de l'acide malique. En déduire la vitesse volumique de formation de l'acide lactique.$\quad(0.75\,\text{pt})$

 

4) Déterminer les vitesses volumiques de disparition de l'acide malique aux instants $t_{1}=4\text{ jours}\ $ et $\ t_{2}=20\text{ jours}.$ Comparer les vitesses trouvées puis justifier.$\quad(1.5\,\text{pts})$

Données : masse de la terre : $M_{T}=5.98\cdot 10^{24}\,kg$ ; constante de gravitation $K=6.67\cdot 10^{-11}\,\text{SI}$

 

Masses des planètes du système solaire : (la masse de la terre étant prise égale à l'unité).

$$\begin{array}{|c|c|c|c|c|c|c|c|c|}\hline\text{Terre}&\text{Mercure}&\text{Vénus}&\text{Mars}&\text{Jupiter}&\text{Saturne}&\text{Uranus}&\text{Neptune}&\text{Lune}\\ \hline 1&0.056&0.817&0.11&318&95.2&14.6&17&0.012\\ \hline\end{array}$$

Au cours de son exploration du système solaire, une sonde Voyager, de masse $M=2\,100\;Kg$, s'est approchée d'une planète notée $A.$ On a mesuré à deux altitudes différentes comptée à partir du sol de cette planète la force de gravitation exercée par celle-ci sur la sonde soit :

 

$\centerdot\ $ à l'altitude $z_{1}=8\,499\;Km$ on a trouvé $F_{1}=13\,236.51\;N$

 

$\centerdot\ $ à l'altitude $z_{2}=250\,000\;Km$ on a trouvé $F_{2}=189.25\;N$

 

1) Calculer le diamètre moyen de la planète $A.\quad(1\,\text{pt})$

 

2) Quelle est l'intensité du champ de gravitation au niveau du sol de la planète $A\ ?\quad(1.5\,\text{pts})$

 

3) Quelle est le nom de la planète $A\ ?\quad(1\,\text{pt})$

 

4) Neptune de rayon $R_{N}=24.3\cdot 10^{3}\,Km$, possède un satellite dont la période de révolution autour d'elle (sur une trajectoire supposée circulaire) vaut $T_{S}=5\,j\ 21\,h\ 03\,min.$

 

Calculer la distance séparant le centre du satellite au centre de Neptune.$\quad(1\,\text{pt})$

 

Déterminer le travail de la force de gravitation qui s'applique sur le satellite lorsque celui-ci passe du sol de Neptune à l'altitude $z.$ En déduire l'énergie potentielle de gravitation si l'état de référence est pris sur le sol de Neptune de rayon $R_{N}=24.3\cdot 10^{3}\;Km\quad(1.5\,\text{pts})$

Données : $\text{électron }\left\lbrace\begin{array}{rcl}\text{masse }m&=&9.109\times 10^{-31}\;Kg\\ \text{charge }-\mathrm{e}&=&-1.602\times 10^{-19}\;C\\k&=&8.988\times 10^{9}\;\text{SI}\end{array}\right.$

 

L'électron n'est pas relativiste.

 

1) Rutherford a décrit l'atome d'hydrogène par un modèle planétaire : l'électron a un mouvement circulaire, de rayon $r$, autour du noyau constitué d'un proton.

 

La force électrostatique subie par l'électron est dirigée selon la droite proton-électron, attractive, de valeur $f=k\dfrac{\mathrm{e}^{2}}{r^{2}}.$ La force gravitationnelle est négligeable devant cette force électrostatique.

 

1.1) Démontrer que le mouvement de l'électron est uniforme.

 

1.2) Établir l'expression de sa vitesse $v$ en fonction de $k\;,\ \mathrm{e}\;,\ r\ $ et $\ m.$

 

1.3) Exprimer son énergie cinétique en fonction des mêmes paramètres.

 

1.4) Exprimer son énergie mécanique $E$ en fonction de $k\;,\ \mathrm{e}\;,\ r$, sachant que son énergie potentielle est $E_{p}=-\dfrac{k\mathrm{e}^{2}}{r}.$ Quelle est sa limite quand $r$ tend vers l'infini ?

 

2) Différents faits expérimentaux, ont conduit Niels Bohr à formuler l'hypothèse suivante : l'électron ne peut se déplacer que sur certains cercles dont les rayons $r_{n}$ obéissent à la loi :

 

$$v_{n}\times r_{n}=n\times\dfrac{h_{r}}{m}$$

 

$h_{r}\ :$ Constante de Dirac : $h_{r}=1.054\times 10^{-34}\;J.s$

 

$n\ :$ nombre entier $\geq 1$

 

$v_{n}\ :$ vitesse de l'électron sur le cercle de rayon $r_{n}.$

 

2.1) Déterminer l'expression de $r_{n}$ en fonction des constantes $k\;,\ h_{r}\;,\ m\;,\ \mathrm{e}$ et de $n.$

 

Exprimer $r_{n}$ en fonction de $r_{1}.$ Calculer $r_{1}.$

 

2.2) Déterminer l'expression de $E_{n}$, énergie mécanique de l'électron sur le cercle de rayon $r_{n}$, en fonction des mêmes paramètres. Exprimer $E_{n}$ en fonction de $E_{1}.$

 

2.3) Calculer $E_{1}\ $ et $\ E_{2}$ en électron-volts. Quelle cause peut faire passer l'énergie de l'électron de $E_{1}\ $ à $\ E_{2}\ ?$

 

$$\text{Durée 2 heures}$$