Bac Maths D, Tunisie 2018
Exercice 1
1. Soit le plan $(\mathcal{Q})$ d'équation $x+y+\sqrt{2}z-2=0$
Montrer que le plan $(\mathcal{Q})$ coupe les axes $(O\;,\ \vec{i})$ ; $(O\;,\ \vec{j})$ ; $(O\;,\ \vec{k})$, respectivement aux points $A(2\;,\ 0\;,\ 0)$, $B(0\;,\ 2\;,\ 0)$ et $C(0\;,\ 0\;,\ \sqrt{2}).$
2. Soit la sphère $(\mathcal{S})$ d'équation $x^{2}+\sqrt{2}+z_{2}=1.$
Montrer que le plan $\mathcal{Q}$ et la sphère $(\mathcal{S})$ sont tangentes et déterminer leur points de contact.
3. Soit $a$ un réel strictement positif.
On considère les points $M(a\ ;\ 0\ ;\ 0)$ et $N\left(0\;,\ \dfrac{4}{\alpha}\ ;\ 0\right).$
Déterminer en fonction du réel a, les composantes du vecteur $\overrightarrow{CM}\wedge\overrightarrow{CN}.$
4. a) Montrer qu'une équation du plan $(CMN)$ est $4x+a^{2}y+2a\sqrt{2}z-4a=0.$
b) Soir d la distance du point $O$ au plan $(CMN).$
Montrer que $d=1-\dfrac{(a−2)^{2}}{a^{2}+4}.$
c) En déduire la valeur du réel $a$ pour laquelle la distance $d$ est maximale.
5. a) Montrer que pour tout réel $a>0$, le volume du tétraèdre $OCMN$ est égal à $\dfrac{2\sqrt{2}}{3}.$
b) En déduire que pour tout réel $a>0$, l'aire du triangle $CMN$ est supérieure ou égale à $2\sqrt{2}.$
c) Identifier les points $M$ et $N$ pour lesquels l'aire du triangle $CMN$ est égale à $2\sqrt{2}.$
Exercice 2
le client lance un dé cubique équilibré dont une face porte la lettre $G$, deux faces portent la lettre $R$ et trois faces portent la lettre $D.$
$-\ $si la face supérieure du dé porte $G$, le client reçoit un montant de $100\ DT$ et le jeu s'arrête.
$-\ $Si la face supérieure du dé porte $R$, le client ne reçoit rien et le jeu s'arrête.
$-\ $Si la face supérieure du dé porte $D$, le client effectue un deuxième lancer ; si la face supérieure du dé au deuxième lancer porte $G$, le client reçoit un montant de $50\ DT$ et si la face supérieure du dé au deuxième lancer porte l'une des lettres $R$ ou $D$, le client ne reçoit rien et le jeu s'arrête.
On considère les évènements suivants :
$G_{1}$ : « Le client reçoit un montant de $100\ DT$ »
$G_{2}$ : « Le client reçoit un montant de $50\ DT$ ».
1. a) Déterminer $p\left(G_{1}\right)$, la probabilité de l'évènement $G_{1}.$
b) Montrer que $p\left(G_{2}\right)=\dfrac{1}{12}.$
c) En déduire que la probabilité qu'un client reçoit un montant non nul est égale à $\dfrac{1}{4}.$
2. On désigne par $X$ la variable aléatoire qui associe le montant reçu par un client lors de sa participation à ce jeu.
$(X$ prend la valeur $0$ lorsque le client ne reçoit rien$).$
a) Déterminer la loi de probabilité de $X.$
b) Calculer $E(X)$, le montant moyen à recevoir par un client.
3. On suppose que $200$ clients ont participé à ce jeu.
On désigne par $Y$ la variable aléatoire donnant le nombre de client ayant reçu un montant non nul et $E(Y)$ le nombre moyen de clients gagnants.
Déterminer, en justifiant, $E(Y).$
4. Le gérant de ce magasin a prévu $1200\ DT$ comme montant global à distinguer.
Le gérant a-t-il bien estimé ce montant ?
Exercice 3
(On donnera les solutions sous forme exponentielle).
2. Pour tout $z\in\mathbb{C}$, on pose $p(z)=3z^{4}-7\mathrm{i}\sqrt{3}z^{3}-18z^{2}+7\mathrm{i}\sqrt{3}z+3.$
a) Vérifier que $p(\mathrm{i}\sqrt{3})=0$ et que $p\left(\mathrm{e}^{\mathrm{i}\left(\dfrac{2\pi}{3}\right)}\right)=0$
b) Montrer que pour tout nombre complexe non nul $z$, $p\left(\dfrac{-1}{z}\right)=\dfrac{1}{z^{4}}\cdot p(z).$
c) En déduire que les nombres $\dfrac{\sqrt{3}}{3}\mathrm{i}$ et $\left(\mathrm{e}^{\mathrm{i}\left(\dfrac{2\pi}{3}\right)}\right)$ sont deux solutions de l'équation $p(z)=0.$
3. Le plan est muni d'un repère orthonormé direct $(O\;,\ \vec{u}\;,\ \vec{v}).$
On désigne par $A$, $B$ et $C$ les points d'affixes respectives $\mathrm{e}^{\mathrm{i}\dfrac{\pi}{3}}$ ; $3\mathrm{e}^{\mathrm{i}\dfrac{\pi}{3}}$ ; $\mathrm{e}^\mathrm{i}\left(\dfrac{2\pi}{3}\right).$
a) Construire les points $A$, $B$ et $C.$
b) Construire le point $D$ défini par $\overrightarrow{OD}=\overrightarrow{OA} +\overrightarrow{OC}$ et donner son affixe sous la forme cartésienne.
c) La parallèle à la droite $(BD)$ passant par $A$ coupe la droite $(OD)$ au point $E.$
Déterminer l'affixe du point $E.$
Exercice 4
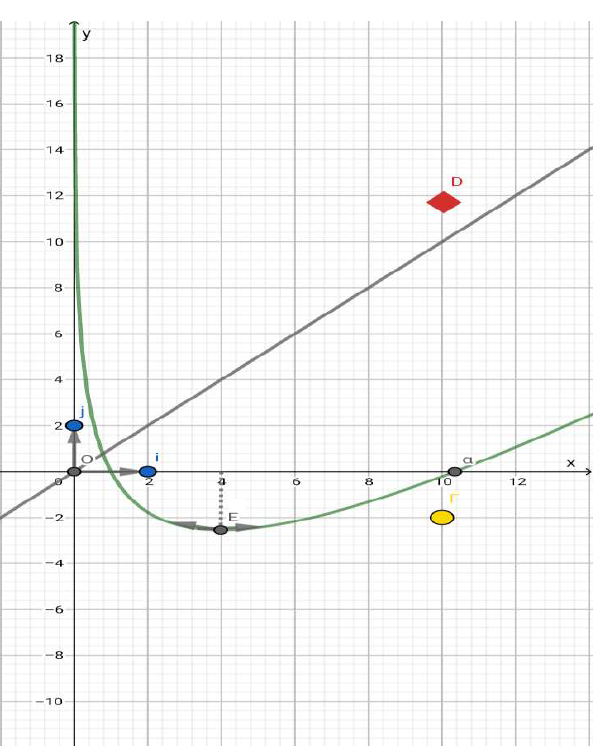
$(\Gamma)$ est la courbe représentative de la fonction $u$ définie sur $I=]0\ ;\ +\infty[$ par : $u(x)=x-1-4\ln x$, l'axe des ordonnées est une asymptote à $(\Gamma).$
La droite $D\ :\ y=x$ est une asymptote à $(\Gamma)$ admet une unique tangente horizontale au point d'abscisse $4.$
La courbe $(\Gamma)$ coupe l'axe $(O\ ;\ \vec{j})$ en deux points d'abscisses respectives $1$ et $\alpha.$
A. Déterminer graphiquement
1. $U(1)$ ; $u(\alpha)$ ; $u'(4)$, $\lim\limits_{\to +\infty}u(x)$ ; $\lim\limits_{\to 0^{+}}u(x)$ ; $\lim\limits_{\to +\infty}\dfrac{u(x)}{x}$
2. Les signes respectives de $u(x)$ et $u'(x).$
B. On considère la fonction $f$ définie sur $J=f(x)=\dfrac{\mathrm{e}^{x}−1}{x^{4}}-(x-1)+4\ln x.$
On désigne par $(\mathcal{C})$ sa courbe représentative dans le repère $(O\;,\ \vec{i}\;,\ \vec{j}).$
1. a) Vérifier que pour tout $x\in J\;,\ f'(x)=\mathrm{e}^{u(x)}-u(x).$
b) Calculer $f(\alpha).$
c) Montrer que $\lim\limits_{\to 0^{+}}f(x)$ et $\lim\limits_{\to +\infty}f(x).$
d) Montrer que $\lim\limits_{\to +\infty}\dfrac{f(x)}{x}=+\infty.$
e) Donner les branches infinies de la courbe $(\mathcal{C}).$
2. a) Vérifier que pour tout $\in J\;,\ f'(x)u'(x)\cdot(\mathrm{e}^{u(x)}-1).$
b) Justifier que $f'(x)>0$, si et seulement si, $x\in ]1\ ;\ 4[\cup ]\alpha\ ;\ +\infty[.$
c) Dresser le tableau de variation de $f.$
3. a) Montrer que pour tout réel $x\;,\ \mathrm{e}^{x}-2x>0.$
b) Déduire la position relative de $(\mathcal{C})$ et $(\Gamma).$
c) Tracer dans l'annexe la courbe $(\mathcal{C}).$
4. On désigne par $A$ l'aire de la partie du plan limité par la courbe $(\mathcal{C})$ et les droites d'équations $x=3$ ; $x=5$ et $y=0.$
$A'$ l'aire de la partie du plan limité par la courbe $(\Gamma)$ et les droites d'équations $x=3$, $x=5$ et $y=0.$
a) Montrer que $A'=20\ln 5-12\ln 3-14.$
b) Montrer que $A'<A<2f(4).$
En déduire que $5<A<5.25.$
Annexe à rendre avec la copie

Ajouter un commentaire