Bac Maths D, Tunisie 2014

Soit $f$ la fonction définie sur $\mathbb{R}$ par $f(x)=\dfrac{\mathrm{e}^{x}}{1+\mathrm{e}^{x}}.$
 
On désigne par $\mathcal{C_{f}}$ la courbe représentative de $f$ dans un repère orthonormé  $(O\;,\ \vec{i}\;,\ \vec{j}).$

1. a) Calculer $\lim\limits_{x\to +\infty}f(x).$

b) Calculer $\lim\limits_{x\to -\infty}f(x)$ et montrer que $\lim\limits_{x\to -\infty}\dfrac{f(x)}{x}=-\infty.$

Interpréter graphiquement ce résultat.

2. a) Montrer que pour tout réel $x$, $f'(x)=-\dfrac{(2+\mathrm{e}^{−x})}{ (1+\mathrm{e}^{x})^{2}}.$      

b) Dresser le tableau de variation de $f.$

3. a) Justifier que la tangente $(\mathcal{T})$ à la courbe $\mathcal{C_{f}}$ au point d'abscisse $0$ a pour équation $y=-\dfrac{3}{4}x+\dfrac{1}{2}.$      

b) Utiliser le tableau de signe ci-contre pour préciser la position relative de $\mathcal{C_{f}}$ et $(\mathcal{T}).$
$$\begin{array}{|c|lcccr|} \hline x&-\infty&&0&&+\infty\\  \hline f'(x)+\dfrac{3}{4}&&-&|&+&\\ \hline  \end{array}$$

c) Tracer $(\mathcal{T})$ et $\mathcal{C_{f}}.$

4. Soit $\lambda$ un réel strictement positif.

On désigne par $\mathcal{A}\lambda$ l'aire de la partie du plan limitée par la courbe $\mathcal{C_{f}}$, les axes du repère et la droite d'équation $x=\lambda.$

a) Vérifier que, pour tout réel $x$, $f(x)=\mathrm{e}^{-x}-\dfrac{\mathrm{e}^{-x}}{1+\mathrm{e}^{-x}}.$

b) Montrer que $\mathcal{A}\lambda=\mathrm{e}^{-\lambda}+\ln(1+\mathrm{e}^{-\lambda})+1-\ln 2.$

c) Calculer $\lim\limits_{x\to +\infty}\mathcal{A}\lambda.$

En vue de comprendre le phénomène de refroidissement d'un liquide après son ébullition, on relève, durant une heure et toutes les $5$ minutes, la température $T$ de ce liquide.

Le tableau ci-dessous donne les résultats recensés pour une tasse de café servie dans un salon dont la température ambiante est de $20^{\circ}C.$
$$\begin{array}{|l|c|c|c|c|c|c|c|c|c|c|c|c|c|} \hline t\text{ (en mn)}&0&5&10&15&20&25&30&35&40&45&50&55&60\\ \hline  T\text{ (en }^{\circ}C)&100&68.5&50&37.8&31&26.5&24&22&21.5&20.9&20.5&20.3& 20.2\\ \hline \end{array}$$

On pose $\theta=\ln(T-20).$

Les valeurs de $\theta$ ; arrondie à $10^{-2}$ près, sont données dans le tableau qui suit :
$$\begin{array}{|l|c|c|c|c|c|c|c|c|c|c|c|c|c|} \hline t\text{ (en mn)}&0&5&10&15&20&25&30&35&40&45&50&55&60\\ \hline  T\text{ (en}^{\circ }C) &4.38&3.88&3.40&2.88&2.40&1.87&1.39&0.69&0.41&-0.10& -0.69&-1.2&-1.60\\ \hline \end{array}$$

1. a) Construire le nuage de point de la série $(t\;,\ \theta)$, dans la repère proposé dans l'annexe ci-jointe (Figure 1).

b) Calculer le coefficient de corrélation linéaire $r$ de la série $(t\;,\  \theta).$

Interpréter le résultat.

2. a) Donner une équation de la droite de régression de $\theta$ en $t.$       

$($On donnera les coefficients de cette équation arrondis à $10^{-2}$ près$).$       

b) En déduire que l'expression de $T$ en fonction de $t$ est de la forme $T=20+\alpha\mathrm{e}^{\beta t}$, $\alpha$ et $\beta$ étant deux réels dont on donnera les valeurs respectives arrondies à $10^{-1}$ près.       

c) Estimer la température de cette tasse de café après $90$ minutes de sa préparation.        

d) La température de cette tasse de café atteindra-t-elle $18^{\circ}C$ ?

Expliquer.

L'espace est rapporté à un repère orthonormé $(O\;,\ \vec{i}\;,\ \vec{j}\;,\ \vec{k}).$

On considère la sphère $(\mathcal{S})$ d'équation $x^{2}+y^{2}+z^{2}-8=0$ et le plan $\mathcal{P}$ d'équation : $x+2y+z\pm 6=0.$

1. a) Déterminer le centre et le rayon de la sphère $(\mathcal{S}).$

b) Montrer que le plan $\mathcal{P}$ coupe la sphère $(\mathcal{S})$ suivant un cercle $(\mathcal{C})$ dont on précisera le centre et le rayon.

2. On donne les points $A(2\;,\ 0\;,\ 2)$ et $B(2\;,\ 2\;,\ 0).$

a) Vérifier que $A$ appartient à la sphère $(\mathcal{S})$ et n'appartient pas au plan $\mathcal{P}$ et que $B$ appartient au cercle $(\mathcal{C}).$

b) Soit $\mathcal{Q}$ l'ensemble des points$M(x\ ;\ y\ ;\ z)$ de l'espace tels que $MA=MB.$      

Montrer que $\mathcal{Q}$ est le plan d'équation $y=z.$

c) Montrer que les plans $\mathcal{P}$ et $\mathcal{Q}$ se coupent suivant la droite $\Delta$ dont une représentation paramétrique est
$$\left\lbrace\begin{array}{lcl} x&=&6-3\alpha\\ y&=&\alpha\;,\quad\alpha\in\mathbb{R}\\ z&=&\alpha \end{array}\right\rbrace$$

3. Déterminer un point $C$ du cercle $(\mathcal{C})$ tel que $ABC$ est un triangle équilatéral.

1. soit les nombres complexes $z_{1}=\dfrac{\sqrt{5}}{2}-\mathrm{i}\dfrac{\sqrt{3}}{2}$  et  $z_{2}=-\dfrac{\sqrt{5}}{2}-\mathrm{i}\dfrac{\sqrt{3}}{2}.$

a) Calculer $z_{1}+z_{2}$  et  $z_{1}\times z_{2}.$

b) En déduire que, pour tout nombres complexe $z\;,\ (z-z_{1})(z-z_{2})=z^{2}+\mathrm{i}\sqrt{3}z-2.$

Dans la suite, on muni le plan complexe d'un repère orthonormé direct $(O\;,\ \vec{u}\;,\ \vec{v})$ et on considère les points $M_{1}$ et $M_{2}$ d'affixes respectives $z_{1}$ et $z_{2}.$

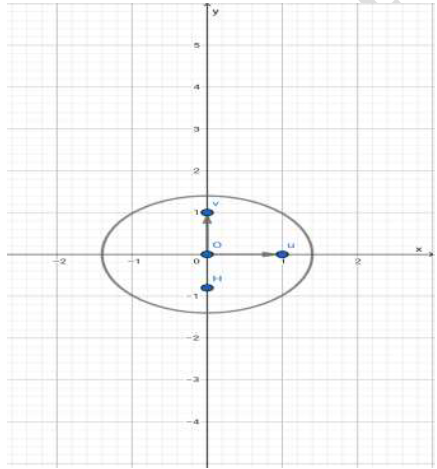
2. Dans l'annexe ci-jointe (Figure 2), on a tracé le cercle $(\mathcal{C})$ de centre $O$ et de rayon $\sqrt{2}$ et on a placé le point $H$ d'affixe $\dfrac{-\mathrm{i}\sqrt{3}}{2}.$

a) Montrer que $M_{1}$ et $M_{2}$ appartiennent à $(\mathcal{C}).$

b) Justifier que $H$ est le milieu du segment $\left[M_{1}M_{2}\right].$

c) Construire les points $M_{1}$ et $M_{2}.$

3. Soit $K$ le point d'affixe $−\mathrm{i}\sqrt{3}.$

Soit $z$ un nombre complexe et $M$ et $N$ les points du plan complexe d'affixes respectives $z$ et $z^{3}.$

a) Montrer que : $(K$ est le milieu du segment $[MN]$ si et seulement si $z^{3}+z+2\mathrm{i}\sqrt{3}=0).$

b) Vérifier que $z^{3}+z+2\mathrm{i}\sqrt{3}=(z-\mathrm{i}\sqrt{3})(z^{2}+\mathrm{i}\sqrt{3}z-2).$

c) Résoudre dans $\mathbb{C}$ l'équation $z^{2}+z+2\mathrm{i}\sqrt{3}=0.$

d) Construire alors les points $N_{1}$ et $N_{2}$ d'affixes respectives $z^{3}_{2}$ et $z^{3}_{2}$

$($On rappelle que $z_{1}$ et $z_{2}$ sont les affixes des points $M_{1}$ et $M_{2}).$

e) Déterminer l'affixe a d'un point $A$ de l'axe $(O\;,\ \vec{v})$ dont le symétrique par rapport au point $K$ est d'affixe $a^{3}$

Figure 1

L'axe des ordonnés $\theta$ n'est pas représentée en vrai grandeur.