Bac Maths D, Tunisie 2013

Dans la figure ci-dessous, $ABCDEFGH$ est un cube d'arrêt $1.$
 
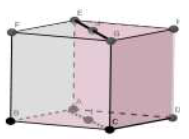
Le point $I$ est le milieu du segment $[AC].$
 
Le point $J$ est le milieu du segment $[EG].$

L'espace est muni du repère orthonormé direct $(A\ ;\ \overrightarrow{AB}\;,\ \overrightarrow{AD}\;,\ \overrightarrow{AE}).$

 
Répondre par vrai ou faux à chacune des propositions suivantes en justifiant la réponse.

1. $\overrightarrow{AC}\wedge\overrightarrow{BD}=\overrightarrow{AE}.$
 
2. $(\overrightarrow{IA}\wedge\overrightarrow{IG})\cdot\overrightarrow{IJ}= 0.$

3. La sphere de diamètre  $[AC]$ est tangente au plan d'équation $z-1=0.$

I. Dans la figure ci-dessous, on a représenté dans un repère orthogonal $(O\;,\ \vec{i}\;,\ \vec{j})$ la courbe $\mathcal{C_{f}}$ de la fonction $f$ définie sur $\mathbb{R}$ par $f(x)=x^{3}+6x+2.$

1. Justifier que l'équation $x^{3}+6x+2=0.$

Admet dans $\mathbb{R}$ une solution unique $\alpha.$

 
2. Donner un encadrement de $\alpha$ d'amplitude $10^{-1}.$
 
II. On se propose dans cette partie de déterminer la valeur de $\alpha.$

1. On considère dans $\mathbb{C}$ les équations $\left(E_{1}\right)\ :\ z^{3}=2$ et $\left(E_{1}\right)\ :\ z^{3}=−4.$

a) Justifier que les solutions de $\left(E_{1}\right)$ sont :

$a_{1}=\sqrt[3]{2}\ ;\ a_{2}=\sqrt[3]{2}\mathrm{e}^{\mathrm{i}\dfrac{2\pi}{3}}\ ;\ a_{3}=\sqrt[3]{2}\mathrm{e}^{\mathrm{i}\left(\dfrac{2\pi}{3}\right)}.$

b) Justifier que les solutions de $\left(E_{2}\right)$ sont $b_{1}=-\sqrt[3]{4}\ ;\ b_{2}=\sqrt[3]{4}\mathrm{e}^{\mathrm{i}\dfrac{\pi}{3}}\text{ et }b_{3}=\sqrt[3]{4}\mathrm{e}^{\mathrm{i}\left(\dfrac{-\pi}{3}\right)}.$

c) Vérifier que $a_{1}b_{1}=a_{2}b_{2}=a_{3}b_{3}=−2.$

2. Soit $a$ et $b$ deux nombres complexes vérifiant $a^{3}+b^{3}=−2$ et $ab=−2.$

a) Vérifier que $(a+b)^{3}=−2-6(a+b).$

b) En déduire que $a+b$ est une solution de l'équation $z^{3}+6z+2=0.$

3. Déduire les solutions de l'équation $z^{3}+6z+2=0.$

4. Conclure.

Une étude a été faite sur une population de $22$ mouches se reproduisent assez rapidement.

Le tableau suivant donne le nombre $N$ de mouches après un temps $T$ exprimé en jours.
$$\begin{array}{|l|c|c|c|c|c|c|c|c|c|c|c|c|} \hline T&0&9&12&18&25&33&39&48&57&66&69&75\\ \hline M&22&39&105&225&499&791&938&1005&1028&1033&1034&1034\\ \hline  \end{array}$$

1. Quelle conjecturer peut-on émettre sur le nombre de mouches au bout de $85$ jours ?

2. On pose $M=\ln\left(\dfrac{1035}{N}-1\right).$

Les valeurs de $M$, arrondies à $10^{-3}$ près, sont données dans le tableau suivant :
$$\begin{array}{|l|c|c|c|c|c|c|c|c|c|c|c|c|} \hline T&0&9&12&18&25&33&39&48&57&66&69&75\\ \hline M&3.830&3.240&2.181&1.281&0.072&-1.176&-2.269&-3.512&-4.989&-6.247&-6.941&-6.941\\  \hline \end{array}$$

a) Donner une valeur approchée à $10^{-3}$ près du coefficient de corrélation linéaire en $T$ et $M$.

b) Donner une équation de la droite de régression de $M$ en $T$ $($les coefficients seront arrondies à $10^{-3}$ près$).$

3. a) Montrer que $N=\dfrac{1035}{1+\mathrm{e}^{M}}.$

b) Déduire que $N=\dfrac{1035}{1+\alpha\mathrm{e}^{-\beta T}}$, où $\alpha$ et $\beta$ sont deux réels positifs que l'on déterminera.

4. En utilisant la question 3. b), valider ou réfuter la conjecture émise en $1.$

Dans l'annexe ci-jointe $(O\;,\ \vec{i}\;,\ \vec{j})$ est un repère orthonormé et $\mathcal{C_{f}}$ est la courbe représentative de la fonction $f$ définie sur $[3\ ;\ +\infty[$ par $f(x)=\ln x+\sqrt{x^{2}-9}.$

Soit $E$ la partie du plan limitée par la courbe $\mathcal{C_{f}}$ et les droites d'équations $x=9$, et $x=5$ et $y=\ln 3.$

On désigne par $\mathcal{A}$ l'aire (en unité d'aire) de $E.$

1. Hachurer $E.$

2. a) Vérifier que $f(5)=2\ln 3.$

b) Soit $M$ et $N$ les points de la courbe $\mathcal{C_{f}}$ d'abscisse respectives $3$ et $5$ et $P$ et $Q$ les points de coordonnées respectives $(5\;,\ \ln 3)$ et $(3\;,\ 2\ln 2).$

Placer, dans le repère $(O\;,\ \vec{i}\;,\ \vec{j})$, les points $M$, $N$, $P$ et $Q.$

c) Calculer l'aire du rectangle $MPNQ$ et l'aire du triangle $MPN.$

d) En déduire que $\ln 3\leq\mathcal{A}\leq 2\ln 3.$      

3. a) Calculer $\lim\limits_{\to +\infty}f(x)$

b) En utilisant le graphique, justifier que $f$ réalise une bijection de $[3\ ;\ +\infty[$ sur l'intervalle $[\ln 3\;,\ +\infty[.$
 
4. Soit $g$ la fonction réciproque de la fonction $f$ et $\mathcal{C_{g}}$ sa courbe représentative dans le repère $(O\;,\ \vec{i}\;,\ \vec{j})$

Tracer la courbe $\mathcal{C_{g}}.$
 
5. Soit $E'$ la partie du plan limitée par la courbe $\mathcal{C_{g}}$ et les droites d'équations : $x=\ln 3\;,\ x=2\ln 3$ et $y=5.$  

On désigne par $\mathcal{A'}$ l'aire (en unité d'aire) de $E'.$

a) Hachurer $E'.$

b) Montrer que $$\mathcal{A'}=5\ln 3-\int^{2\ln 3}_{\ln 3}g(x)\mathrm{d}x.$$
 
6. a) Montrer que pour tout réel $x$ de l'intervalle $[\ln 3\;,\ +\infty[\;,\  g(x)\dfrac{\mathrm{e}^{x}+9\mathrm{e}^{-x}}{2}.$

b) Calculer $$\int^{2\ln 3}_{\ln 3}g(x)\mathrm{d}x$$ et en déduire la valeur de $\mathcal{A}.$