Exercices : Le carré - 5e
Classe:
Cinquième
Exercice 1
Complète les phrases ci-dessous par les expressions qui conviennent.
1) Un quadrilatère qui a quatre angles …… et quatre côtés de même …… est un carré.
2) Un quadrilatère qui a ses côtés consécutifs …… et de même longueur est un carré.
3) Un quadrilatère qui a ses …… perpendiculaires et de même …… est un carré.
4) Un quadrilatère qui possède un centre et quatre …… de symétrie est un carré.
Exercice 2
Recopie et complète les phrases ci-dessous à l'aide des mots suivants : rectangle, longueur, carré, consécutifs, losange, perpendiculaires, diagonales.
1) Si un …… a un angle droit alors c'est un ……
2) Si un rectangle a deux côtés …… de même …… alors c'est un carré.
3) Si un losange a ses …… de même …… alors c'est un …….
4) Si un …… a ses diagonales …… alors c'est un carré.
Exercice 3
1) Citer deux parmi les propriétés du carré.
2) Comment reconnaître un carré ? Donner deux exemples.
Exercice 4
1) Construire un cercle (C) de centre O et de rayon r=2.5cm.
2) Les segments [AC] et [BD] sont deux diamètres à supports perpendiculaires du cercle (C).
3) Quelle est la nature de ABCD ? Justifier.
Exercice 5
1) Construire un carré ABCD de coté 3cm.
2) Construire les points E et F symétriques respectifs des sommets B et D par rapport à A.
3) Quelle est la nature du quadrilatère BDEF ? Justifier la réponse.
4) Calculer l'aire de BDEF.
Exercice 6
1) a) Construire un triangle ABO tel que : AO=4cm; mesˆA=45∘ et mesˆO=30∘.
b) Calculer mes B puis en déduire la nature de ABO.
2) Marquer les points D et C : SB(A)=D et SB(O)=C.
3) Quelle est la nature de OACD ? Justifier.
4) a) Construire le cercle (C1) circonscrit à ABO.
b) Construire le cercle (C2) circonscrit à OACD.
Exercice 7
1) a) Construire un triangle ABC tel que : AB=4cm; mesˆA=60∘ et mesˆB=30∘.
b) Calculer mesˆC puis en déduire la nature de ABC.
2) a) Construire le cercle (C) circonscrit à ABC.
b) Placer les points D et P tel que : le point D est le milieu du segment [AB] et le point P est le symétrique de C par rapport à D.
3) a) Quelle est la nature de ACBP ? Justifier.
b) Placer le point Q tel que : ABCQ soit un parallélogramme.
Exercice 8
Dans chacun des énoncés ci-dessous, trois affirmations a, b et c sont faites ; choisis la bonne.
1) Si ABCD est un carré, alors les droites :
a) (AB) et (DC) sont perpendiculaires.
b) (AB) et (BD) sont perpendiculaires.
c) (AB) et (AD) sont perpendiculaires.
2) Si ABCD est un carré, alors :
a) AB=CD.
b) AC=AB.
c) AC=CD.
3) Si ABCD est un carré, alors :
a) [AC] et [AB] ont même milieu.
b) (AB) et (AC) sont perpendiculaires.
c) AC=BD.
Exercice 9
Trace un segment [AC] de longueur 8cm puis construis les points B et D tels que ABCD soit un carré
Exercice 10
1) Place deux points I et O distincts puis construis à l'aide de la règle et du compas les points J, K et L tels que IJKL soit un carré de centre O.
2) Place un point P, construis un carré QRST de centre P et de côté 6cm.
Exercice 11
La figure ci-dessous est un rectangle dont les diagonales se coupent au point P avec LP=4cm.
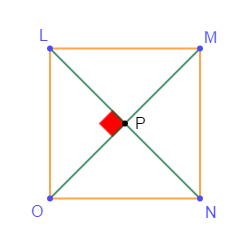
1) Démontre que le quadrilatère LMNO est un carré.
2) Quelles sont les longueurs des segments [LN] et [MO] ?
Justifie la réponse.
Exercice 12
La figure ci-dessous est t-il un carré ? Justifie.
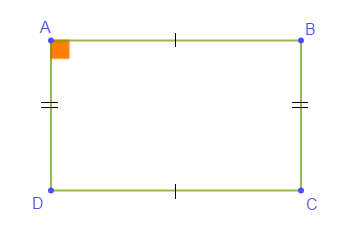
Exercice 13
1) Trace un carré CINQ.
2) Construis les points E et F, symétriques respectifs des points C et N par rapport au point I.
3) Quelle est la nature du quadrilatère CNEF ? Justifie ta réponse.
Exercice 14
Construis un carré EFGH de centre O et le point I symétrique du point O par rapport à la droite (EF).
Démontre que le quadrilatère EOFI est un carré.
Exercice 15
Soit ABCD un carré de centre O et de côté 4cm.
1) Justifie que [AC] et [BD] ont même milieu.
2) Que peut-on dire des droites (AC) et (BD) ?
Exercice 16
1) Construis un triangle ABD rectangle et isocèle en A.
2) Trace le cercle de centre D et passant par le point A. Trace le cercle de centre B et passant par le point A. Ces deux cercles se coupent aux points A et C.
3) Démontre que le quadrilatère ABCD est un carré.
Exercice 17
Dans la figure ci-dessous MATH est un carré de centre G.
Détermine en justifiant, la mesure de l'angle :
a) ^MGA
b) ^MAG
Exercice 18
1) Trace un segment [HM] de longueur 2.5cm
2) Construis un carré HPME de centre le point K.
3) Détermine, en justifiant, la longueur PE.
Auteur:
Diny Faye & adem
Ajouter un commentaire