Bac Maths D, Tunisie 2011

Pour chacune des questions suivantes, une seule des trois réponses proposées est exacte.

Le candidat indiquera sur sa copie le numéro de la question et la lettre correspondant à la réponse choisie.

Aucune justification n'est demandée.

Dans la figure ci-contre $ABCDEFGH$ est un cube d'arrêt $1.$

On munit l'espace du repère $(A\;,\ \overrightarrow{AB}\;,\ \overrightarrow{AD}\;,\ \overrightarrow{AE}).$

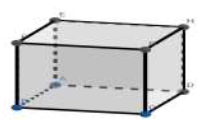
1. Le vecteur $\overrightarrow{BF}\wedge\overrightarrow{BC}$ est égal à  

a. $\overrightarrow{BG}$    

b. $\overrightarrow{BD}$   

c. $\overrightarrow{BA}$       

2. L'intersection des plans d'équations $x=1$ et $y=1$ est la droite      

a. $(CH)$   

b. $(CF)$         

c. $(CG)$      

3. Une équation du plan $(ACE)$ est      

a. $x+y=0$   

b. $x-y=0$     

c. $x-y=1$     

4. L'intersection de la sphère d'équation $x^{2}+y^{2}+z^{2}=2$ avec le plan d'équation $z=1$ est  

a. Un cercle   

b. Un point       

c. L'ensemble vide

Le plan est muni d'un repère orthonormé direct $(O\;,\ \overrightarrow{u}\;,\ \overrightarrow{v}).$

On considère les points $A$ et $B$ d'affixe respectives $a=\dfrac{1}{2}+ \mathrm{i}\dfrac{\sqrt{3}}{2}$ et $b=\dfrac{\sqrt{3}}{2}+\dfrac{1}{2}\mathrm{i}$

1. a) Donner l'écriture exponentielle de chacun des nombres complexe $a$ et $b.$

b) Vérifier que $b^{2}=a.$

2. Soit $C$ le point d'affixe $c=a+b.$

a) Placer les points $A$, $B$ et $C.$

b) Vérifier que $c=\dfrac{\sqrt{2}+\sqrt{6}}{2}\mathrm{e}^{\mathrm{i}\dfrac{\pi}{4}}.$

3. On considère dans $\mathbb{C}$ l'équation $(E)\ :\ z^{2}+z-z=0.$

a) Vérifier que $b$ est une solution de $(E).$

b) On désigne par $d$ la deuxième solution de $(E).$

Montrer que $d=\dfrac{\sqrt{2}+\sqrt{6}}{2}\mathrm{e}^{\mathrm{i}\left(\dfrac{-11\pi}{12}\right)}.$

c) Placer alors, le point $D$ d'affixe $d.$

Dans l'annexe ci-jointe, on a représenté dans un repère orthonormé $(O\;,\ \vec{i}\;,\ \vec{j})$, la courbe $\mathcal{C}$ de la fonction logarithme népérien (« $\ln$ »).

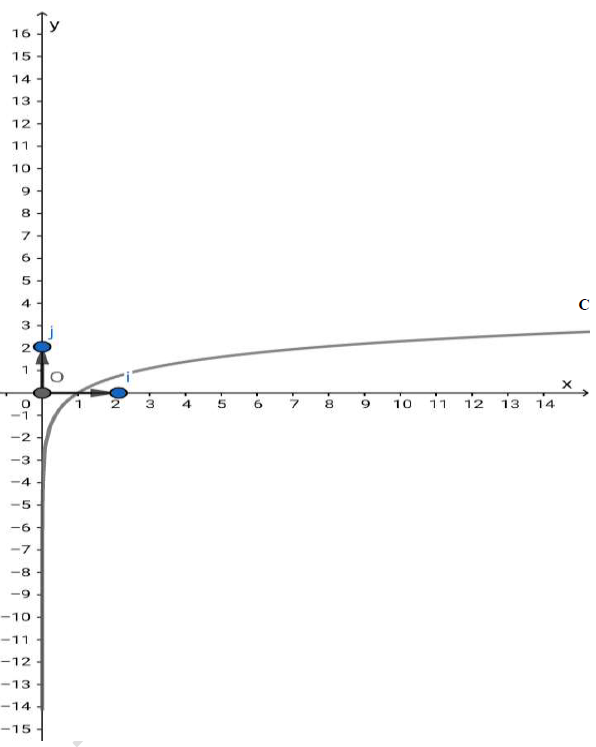
1. Placer les points de la courbe $\mathcal{C}$ d'abscisses $\mathrm{e}$ et $\sqrt{\mathrm{e}}$

2. Soit $f$ la fonction définie sur $I=]0\ ;\ +\infty[$ par $f(x)=\ln 2x-\ln x+1.$

On note $\mathcal{C_{f}}$ sa courbe représentative dans le repère $(O\;,\ \vec{i}\;,\ \vec{j}).$
 
a. Montrer que $\lim\limits_{x\rightarrow 0^{+}}f(x)=+\infty$ et $\lim\limits_{x\rightarrow +\infty}f(x)=+\infty.$
 
b. Calculer $\lim\limits_{x\rightarrow +\infty}\dfrac{f(x)}{x}.$

Interpréter graphiquement le résultat.
 
c. Montrer que pour tout réel $x>0\;,\ f'(x)=\dfrac{2\ln x-1}{x}$
 
d. Dresser le tableau de variation de $f.$       

3. a) Étudier la position relative des courbes $\mathcal{C_{f}}$ et $\mathcal{C}.$             

b) Tracer $\mathcal{C_{f}}$ dans l'annexe ci-jointe.      

4. Soit $\mathcal{A}$ l'aire du plan limité par les courbes $\mathcal{C}$ et $\mathcal{C_{f}}$ et les droites d'équations $x=1$ et $x=\mathrm{e}.$           

a. Montrer que $$\int^{\mathrm{e}}_{1}\ln x\mathrm{d}x=\mathrm{e}-2.$$         

b. Calculer $\mathcal{A}.$

Dans la figure ci-contre on a représenté dans un repère orthonormé la courbe $\mathcal{C_{f}}$ de la fonction $f\ :\ x\mapsto\mathrm{e}^{\dfrac{4}{x}}$ ainsi que la droite $\Delta$ d'équation $y=x.$
 

 
1. a) Utiliser le graphique pour justifier que l'équation $\mathrm{e}^{−\dfrac{x}{4}}=x$ admet dans $J=[0\ ;\ 1]$ une solution unique $\alpha.$
 
b) Vérifier que $0.8<\alpha<0.9.$
 
2. Soit $\left(U_{n}\right)$ la suite définie sur $\mathbb{N}$ par
$$\left\lbrace\begin{array}{lcl} U_{0}&=&1\\ U_{n+1}&=&f\left(U_{n}\right)\ ;\ n\geq 0 \end{array}\right\rbrace$$

a. Montrer que pour tout entier naturel $n\;,\ 0leq U_{n}\leq 1.$
           
b. Montrer que pour tout réel $x\in J\;,\ |f'(x)|\leq\dfrac{1}{4}.$            
                      
c. Montrer que pour tout entier naturel $n\;,\ |U_{n+1}-\alpha|\leq\dfrac{1}{4}|U_{n}-\alpha|.$            

d. En déduire que pour tout entier naturel $n\;,\ |U_{n}-\alpha|\leq \left(\dfrac{1}{4}\right)^{n}.$            

e. Montrer que la suite  $\left(U_{n}\right)$ est convergente vers $\alpha.$    

3. a) Déterminer un entier naturel $n_{0}$ tel que, pour $n\geq n_{0}\;,\ |U_{n}-\alpha|<10^{−3}.$           

b) En déduire une valeur approchée de $\alpha$ à $10^{−3}$ près.