Corrigé BFEM Physique chimie 2009
Exercice 1
La combustion complète de l'acétylène produit une quantité de chaleur qui permet d'atteindre des températures élevées. Cette combustion est utilisée, dans le chalumeau oxyacétylénique, pour effectuer des soudures métalliques.
L'acétylène, encore appelé éthyne, a pour formule brute $C_{2}H_{2}.$
1) L'acétylène appartient à la famille des alcynes
La formule générale des alcynes est :
$$C_{n}H_{2n-2}$$
2) Écrivons l'équation-bilan de la combustion complète de l'acétylène dans le dioxygène.
$$C_{2}H_{2}\ +\ \dfrac{5}{2}O_{2}\ \longrightarrow\ 2CO_{2}\ +\ H_{2}O$$
3) On procède à la combustion complète de $44.8\;L$ du gaz acétylène, volume mesuré dans les conditions normales de température et de pression.
3.1) Calculons le volume de dioxygène gazeux nécessaire pour cette combustion.
Soit : $V_{(O_{2})}=n_{(O_{2})}\times V_{M}$
Or, d'après le bilan molaire, on a : $\dfrac{n_{(C_{2}H_{2})}}{1}=\dfrac{n_{(O_{2})}}{\dfrac{5}{2}}$
Ce qui entraine, $n_{(O_{2})}=\dfrac{5}{2}\times n_{(C_{2}H_{2})}$
Comme $n_{(C_{2}H_{2})}=\dfrac{V_{(C_{2}H_{2})}}{V_{M}}$ alors, en remplaçant, on obtient :
$$n_{(O_{2})}=\dfrac{5}{2}\times \dfrac{V_{(C_{2}H_{2})}}{V_{M}}$$
Par suite,
$\begin{array}{rcl} V_{(O_{2})}&=&n_{(O_{2})}\times V_{M}\\\\&=&\dfrac{5}{2}\times \dfrac{V_{(C_{2}H_{2})}}{V_{M}}\times V_{M}\\\\&=&\dfrac{5\times V_{(C_{2}H_{2})}\times V_{M}}{2\times V_{M}}\\\\&=&\dfrac{5\times V_{(C_{2}H_{2})}}{2}\end{array}$
Ainsi, $\boxed{V_{(O_{2})}=\dfrac{5\times V_{(C_{2}H_{2})}}{2}}$
A.N :$V(O_{2})=\dfrac{5\times 44.8}{2}=112$
D'où, $$\boxed{V(O_{2})=112\;L}$$
3.2) Calculons la quantité de chaleur dégagée lors de cette réaction
Comme la combustion complète d'un litre d'acétylène produit une quantité de chaleur de $58\;kJ$ alors, $112\;L$ va produire une quantité de chaleur $Q$ telle que
$$Q=58\;kJ\times 112=6\,496\;kJ$$
Donc, la quantité de chaleur dégagée lors de cette réaction est :
$$\boxed{Q=6\,496\;kJ}$$
Exercice 2
On prépare une solution d'acide chlorhydrique de volume $V=400\;mL$ en dissolvant $0.24\;mol$ de gaz chlorhydrique dans l'eau pure.
1) Calculons la concentration molaire volumique de la solution d'acide.
Soit : $C=\dfrac{n}{V}$
A.N : $C=\dfrac{0.24}{0.4}=0.6$
Donc, $$\boxed{C=0.6\;mol.L^{-1}}$$
2) Calculons la masse du gaz chlorhydrique dissous.
On sait que : $n=\dfrac{m}{M}\ \Rightarrow\ m=n\times M$
A.N : $m=0.24\times 36.5=8.76$
D'où, $$\boxed{m=8.76\;g}$$
3) Calculons la concentration massique $C_{m}$ de la solution d'acide.
Soit : $C_{m}=\dfrac{m}{V}$
A.N : $C_{m}=\dfrac{8.76}{0.4}=21.9$
Ainsi, $$\boxed{C_{m}=21.9\;g.L^{-1}}$$
4) On prélève $10\;mL$ de la solution d'acide chlorhydrique que l'on dose par une solution d'hydroxyde de sodium de concentration molaire $2\cdot 10^{-1}\;mol.L^{-1}$
Calculons le volume de base versé à l'équivalence.
A l'équivalence on a : $n_{a}=n_{b}$
Or, $n_{a}=C_{a}\times V_{a}\ $ et $n_{b}=C_{b}\times V_{b}$
Donc, $C_{a}\times V_{a}=C_{b}\times V_{b}$
Par suite, $V_{b}=\dfrac{C_{a}\times V_{a}}{C_{b}}$
A.N : $V_{b}=\dfrac{0.6\times 0.01}{2\cdot 10^{-1}}=0.03$
D'où, $$\boxed{V_{b}=0.03\;L}$$
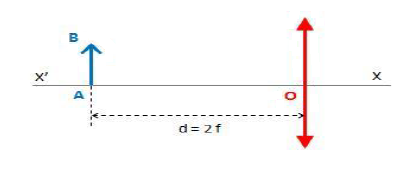
Exercice 3
On considère une lentille convergente de distance focale $f.$
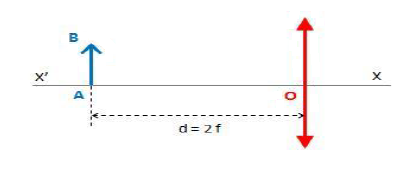
Un objet $AB$ est placé devant la lentille et à une distance $d=2f$ du centre optique $O$ de la lentille, le point $A$ étant situé sur l'axe optique $x'x$, comme indiqué sur le schéma ci-dessus :
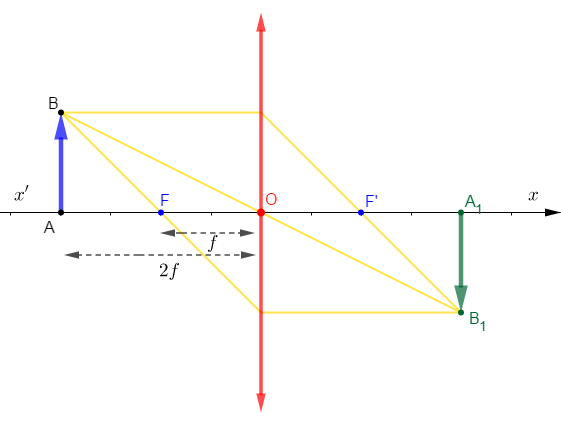
1)Reproduisons le schéma et plaçons les foyers de la lentille puis construisons l'image $A_{1}B_{1}$ de l'objet $AB$ donnée par la lentille.

On constate que $A_{1}B_{1}$ est une image réelle.
2) Déterminons graphiquement le rapport $\left|\dfrac{A_{1}B_{1}}{AB}\right|$
On a : les triangles $ABO\ $ et $\ A_{1}B_{1}O$ sont en position de Thalès.
Donc, en appliquant le théorème de Thalès, on obtient :
$$\left|\dfrac{OA_{1}}{OA}\right|=\left|\dfrac{A_{1}B_{1}}{AB}\right|$$
Comme le point $A$ est situé sur l'axe optique, à une distance $d=2f$ du centre optique $O$, alors son image $A_{1}$ est telle que :
$$|AO|=|OA_{1}|$$
Par suite, $\left|\dfrac{OA_{1}}{OA}\right|=1$
D'où, $$\boxed{\left|\dfrac{A_{1}B_{1}}{AB}\right|=1}$$
3) Soit $f=2\;cm$
Calculons alors la vergence de la lentille
On a : $C=\dfrac{1}{f}$
A.N : $C=\dfrac{1}{0.02}=50$
D'où, $$\boxed{C=50\;\delta}$$
Exercice 4
En travaux pratiques, un groupe d'élèves se propose de vérifier la loi d'Ohm pour un conducteur ohmique.
1)Énonçons la loi d'Ohm :
La tension $U$ aux bornes d'un conducteur ohmique est égale au produit de la résistance $R$ par l'intensité du courant $I$ qui le traverse.
Expression : $U=RI$
2) Faisons l'inventaire du matériel dont le groupe d'élèves a besoin.
$-\ $ Un générateur de tension
$-\ $ Un rhéostat
$-\ $ Des fils de connections
$-\ $ Un conducteur ohmique : résistor
$-\ $ Un interrupteur
$-\ $ Un voltmètre
$-\ $ Un ampèremètre
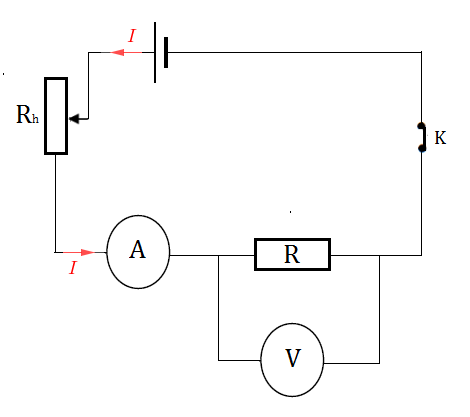
Proposons un schéma de montage :

3) Le conducteur ohmique de résistance $R=20\;\Omega$ est parcouru par un courant d'intensité $I=600\;mA$ durant $t=30$ minutes.
3.1) Calculons la tension aux bornes du conducteur ohmique
D'après la loi d'Ohm, on a : $U=R.I$
A.N : $U=20\times 600\cdot 10^{-3}=12$
Donc, $$\boxed{U=12\;V}$$
3.2) Calculons l'énergie électrique reçue par le conducteur ohmique
Soit : $E=U.I.t$ avec $t$ en seconde
Comme $1\;mn=60\;s$ alors, $t=30\times 60=1800\;s$
A.N : $E=12\times 0.6\times 1800=12\,960$
D'où, $$\boxed{E=12\,960\;J}$$
Cette énergie est dissipée sous forme de chaleur.
Auteur:
Aliou ndiaye

Commentaires
solsiana (non vérifié)
mer, 08/04/2021 - 17:20
Permalien
d`apres mes calcules, 58*112
Ajouter un commentaire