Interférences lumineuses - Ts
Classe:
Terminale
Deux ondes de même de fréquence se propageant dans le même milieu peuvent se superposer pour donner naissance aux phénomènes d'interférences. Si la lumière est une onde, elle doit permettre d'obtenir un tel phénomène
I. Expérience de Young
1. Dispositif expérimentale
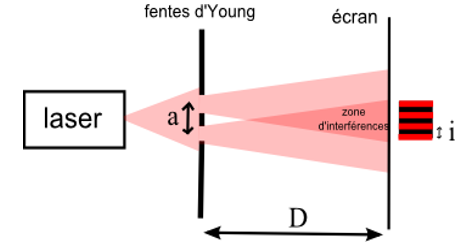
Un faisceau de lumière monochromatique issu d'une source S(laser) est envoyé sur une plaque opaque percée de deux fentes $S_{1}$ et $S_{2}.$ La distance entre les deux fentes est très faible de l'ordre du millimètre.
Un écran est placé derrière la plaque. Il se produit au niveau de chaque fente un phénomène de diffraction. Chacun des fentes $S_{1}$ et $S_{2}$ se comporte comme une source ponctuelle $(S_{1}$ et $S_{2}$ sont des sources secondaires$)$
Les faisceaux issus de $S_{1}$ et $S_{2}$ se superposent dans une certaine région appelée champ d'interférence.
2. Observations
On observe sur l'écran des zones alternativement sombres et claires appelées franges d'interférence. Ces franges au voisinage du point de projection $S$ sur l'écran sont pratiquement rectilignes, parallèles, équidistantes et perpendiculaires au plan de la figure. Ces franges sont observées dans un champ d'interférence quelque soit la position de l'écran : on dit que ces franges sont délocalisées
3. Interprétation
L'existence des franges montre que sous certaines conditions la superposition de deux faisceaux lumineux peut :
$-\ $en certains points, accentuer le phénomène lumineux en donnant des franges brillantes
$-\ $en d'autres points, détruire le phénomène lumineux en donnant des franges sombres.
Le phénomène d'interférence peut s'interpréter si on suppose que les sources secondaires se comportent comme des sources de vibrations de même longueur d'onde.
En point $M$ de l'écran appartenant au champ d'interférence, les vibrations issues de $S_{1}$ et $S_{2}$ arrivent l'une par rapport l'autre avec un certain retard. Ce retard dépend de la différence de marche $\delta=SM_{1}-SM_{2}$
Il y a interférences consstructives en un point de la zone d'interférences si la différence de marche en ce point est un multiple entier de la longueur d'onde : $\delta=k\lambda(k\in\mathbb{R})$
.
Le point $M$ est alors le milieu d'une frange brillante. Il y a interférences destructives en un point de la zone d'interférences si la différence de marche en ce point est un multiple entier impair de la demi-longueur d'onde : $\delta=(2k+1)\dfrac{\lambda}{2}(k\in\mathbb{R})$
$\bullet\ $Le point $M$ est alors le milieu d'une frange sombre
4. Conditions d'interférences
On ne peut obtenir d'interférences lumineuses avec des sources distinctes où on essaie de superposer les faisceaux. Pour obtenir des franges d'interférences, il faut deux sources cohérentes Deux sources sont cohérentes si :
$-\ $elles émettent des vibrations de même fréquence(même période). On dit qu'elles sont synchrones
$-\ $elles présentent une différence de phase constante
$-\ $le rapport d'amplitude constant
II. Interfrange
1. Différence de marche
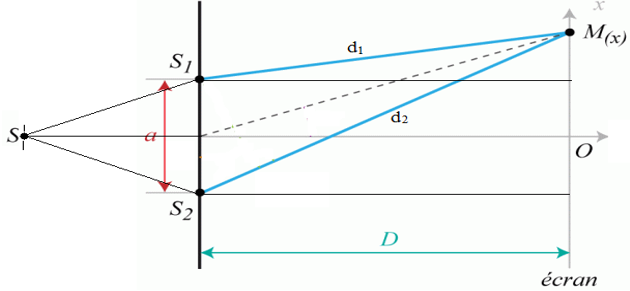
La différence de marche $($notée $\sigma)$ est la différence de distance parcourue par les deux ondes avant d'arriver au point $M$
$\delta=\left(SS_{2}+S_{2}M\right)-\left(SS_{1}+S_{1}M\right)=S_{2}M-S_{1}M\left(SS_{2}=SS_{1}\right)$
$S_{2}M^{2}=d_{2}^{2}=D^{2}+\left(x+\dfrac{a}{2}\right)^{2}$ ;
$S_{1}M^{2}=d_{1}^{2}=D^{2}+\left(x-\dfrac{a}{2}\right)^{2}$ ;
\begin{eqnarray}d_{2}^{2}-d_{1}^{2} &=& D^{2}+\left(x+\dfrac{a}{2}\right)^{2}-\left(D^{2}+\left(x-\dfrac{a}{2}\right)^{2}\right)\nonumber \\\\ &=& D^{2}+\left(x+\dfrac{a}{2}\right)^{2}-D^{2}-\left(x-\dfrac{a}{2}\right)^{2}\end{eqnarray}
\begin{eqnarray} \left(d_{2}-d_{1}\right)\left(d_{2}+d_{1}\right) &=& \left(\left(x+\dfrac{a}{2}\right)+\left(x-\dfrac{a}{2}\right)\right)\left(\left(x+\dfrac{a}{2}\right)-\left(x-\dfrac{a}{2}\right)\right)\nonumber\\\\ &=& 2ax \end{eqnarray}
Les grandeurs $x$ et a sont petites devant la grandeur $D.$ Dans ces conditions
$d_{2}+d_{1}=2D$
$\Rightarrow\delta=d_{2}-d_{1}=\dfrac{2ax}{2D}$
$\Rightarrow\delta=\dfrac{ax}{D}$
2. Position des franges
2.1 Position des milieux des franges brillantes
Les abscisses des milieux des franges brillantes sont tels que :
$$\delta=\dfrac{ax}{D}=k\lambda\Rightarrow x_{k}=k\lambda\dfrac{D}{a}$$
$k=0\Rightarrow x=0$ est l'abscisse du milieu de la frange centrale
$k=1\Rightarrow x_{1}=\lambda\dfrac{D}{a}$ est l'abscisse du milieu de la première frange brillante
$k=2\Rightarrow x_{2}=2\lambda\dfrac{D}{a}$ est l'abscisse du milieu de la deuxième frange brillante
$k=n\Rightarrow x_{n}=n\lambda\dfrac{D}{a}$ est l'abscisse du milieu de la $n^{nième}$ frange brillante
2.2. Position des milieux des franges sombres
Les abscisses des milieux des franges sombres sont tels que :
$$\delta=\dfrac{ax}{D}=(2k+1)\dfrac{\lambda}{2}\Rightarrow x_{k}=(2k+1)\dfrac{\lambda}{2}\dfrac{D}{a}$$
$k=0\Rightarrow x=\dfrac{\lambda}{2}\dfrac{D}{a}$ est l'abscisse du milieu de la de la première sombre
$k=1\Rightarrow x_{1}=\dfrac{3\lambda}{2}\dfrac{D}{a}$ est l'abscisse du milieu de la deuxième frange sombre
$k=n\Rightarrow x_{n}=(2n+1)\dfrac{\lambda}{2}\dfrac{D}{a}$ est l'abscisse du milieu de la $(n+1)^{nième}$ frange sombre
3. Expression de l'interfrange
L'interfrange est la distance qui sépare deux franges consécutives de même nature
$$i=x_{k+1}-x_{k}=(k+1)\lambda\dfrac{D}{a}-k\lambda\dfrac{D}{a}\Rightarrow i=\lambda\dfrac{D}{a}$$

Remarque :
L'ordre d'interférence en un point $M$ de l'écran où la différence de marche est $\delta$, est : $p=\dfrac{\delta}{\lambda}$
$\lambda$ étant la longueur d'onde de la radiation
Si le point $M$ est le milieu d'une frange brillante, on a alors : $p=\dfrac{\delta}{\lambda}=k$
Les franges brillantes ont un ordre d'interférence entier
Si le point $M$ est le milieu d'une frange sombre, on a alors : $p=\dfrac{\delta}{\lambda}=k+\dfrac{1}{2}$
Les franges brillantes ont un ordre d'interférence demi-entier
4. Interférences en lumière blanche
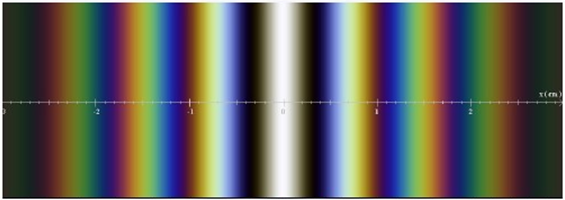
Chacune des lumières monochromatiques formant la lumière blanche donne son propre système de franges (étant incohérente entre elles, elles peuvent interférer).Il y a donc superposition de tous les systèmes de franges.
En particulier, la frange centrale, brillante pour chaque longueur d'onde, apparait donc en blanc. De part et d'autre, on voit des franges colorées de plus en plus décalées, jusqu'à l'œil ne soit plus capables de distinguer les franges sombres du reste (on dit qu'il y a brouillage des franges), ce qui donne une impression de blanc grisâtre (blanc d'ordre supérieur)
III. Spectre de la lumière et applications
1. Le spectre de la lumière
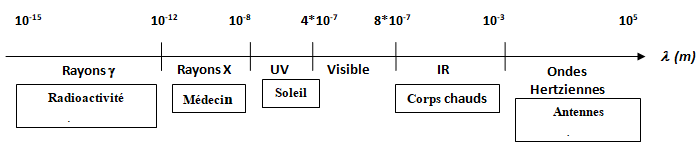
1.1. Le spectre visible
Il est constitué des radiations dans un domaine continu de lumière de longueur d'onde allant du violet $(\lambda=400nm)$ au rouge $(\lambda=800nm)$
1.2. Le rayonnement ultra-violet $(U.V.)$
Il a une longueur d'onde inférieure à $400nm.$ Il est présent dans la haute atmosphère (rayonnement solaire entre autres) et son énergie le rend dangereux . C'est lui qui est responsable du bronzage de la peau et permet la fabrication de la vitamine $D$ de croissance, mais à haute dose, il provoque des brulures et des cancers de la peau.
L'atmosphère terrestre en particulier la couche d'ozone, forme écran et une partie d'entre eux atteint la Terre. La couche d'ozone, protégeant la terre, est donc primondiale, ce qui explique les inquiétudes qui se font jour quant à sa possible disparition.
1.3. Le rayonnement infra-rouge $(I.R.)$
Ces rayonnements sont invisibles pour l'œil humain et transportent de l'énergie thermique. Leur longueur d'onde sont supérieures à $750nm.$ Comme applications, on peut citer les lunettes de nuit, les armes $($les missiles $\mathbb{R})$, la détection par satellite (météorologique militaire...), le diagnostic médical
Remarque :
Les ondes lumineuses, de même les ondes hertziennes, les rayonnements $\mathbb{R}$, $UV$ et les rayons $X$ et $\gamma$ sont des ondes électromagnétiques

2. Applications
Les phénomènes d'interférences dù à la nature ondulatoire de la lumière sont très utilisés dans de nombreux domaines :mesure de la longueur d'onde, d'indice, de faibles épaisseurs, études d'écoulement liquides et gazeux en aérodynamique, résistance des matériaux... L'ensemble de tous ces procédés d'études et de mesures constitue l'interférométrie. Enfin, signalons que les interférences lumineuses sont à la base de la confection des hologrammes ou images en relief, promis à un développement futur important

Ajouter un commentaire