La calorimétrie - 1er s
Classe:
Première
L'énergie transférée à un corps sous forme de travail peut modifier l'énergie cinétique ou l'énergie potentielle de ce corps. Si le corps n'est soumis qu'à des forces extérieures conservatives, son énergie mécanique reste constante. Si le corps n'est soumis en plus à des forces extérieures, son énergie mécanique ne se conserve pas en générale. Dans le cas particulier des forces de frottements, l'énergie mécanique du corps diminue. Mais cette diminution ne se fait pas sans laisser des traces : on constate que le corps s'échauffe ou change d'état.
I. Notion de chaleur
1. Transformation de l'énergie mécanique en énergie thermique sous forme de chaleur
1.1 Étude d'un exemple
Un cycliste pédale sur une pente et freine pour maintenir sa vitesse constante. L'énergie mécanique du système (cycliste et bicyclette) diminue. (L'énergie cinétique demeure constante mais, l'énergie potentielle décroit). On peut constater à la fois de la course qu'il y a échauffement des patins. Nous dirons qu'il y a eu :
$\blacktriangleright\ $diminution de l'énergie mécanique (cycliste et bicyclette)
$\blacktriangleright\ $apparition de l'énergie thermique
1.2. Conclusion
Lorsqu'il existe des forces de frottements au sein d'un système, celui-ci évolue spontanément avec diminution de l'énergie mécanique donc dégradation de l'énergie mécanique
2. Transfert de l'énergie par chaleur
Une casserole métallique contenant de l'eau est placée dans la flamme d'un bruleur de gaz. Nous observons une élévation de température puis sous ébullition à température constante. L'accroissement des énergies potentielles et cinétiques des particules constitutives du système qui conduit à une diminution de la cohésion des molécules et à la vaporisation de l'eau. De l'énergie thermique est transférée de la flamme vers l'eau, de la casserole par chaleur.
3. Définition
Lorsqu'un échange d'énergie a lieu sous forme d'agitation de particules nous l'appelons chaleur. La quantité d'énergie échangée ou quantité de chaleur ou encore quantité d'énergie thermique noté $Q$ s'exprime en joules $(J)$
Autres unité : la calorie $(1Cal)$ : $1Cal=4.18J$
4. Convention de signe
Par convention $Q$ représente la quantité d'énergie échangée.
$\blacktriangleright\ $Si $Q˃0$ (positif) le système reçoit de la chaleur
$\blacktriangleright\ $Si $Q˂0$ (négatif) le système cède de la quantité de chaleur
5. Chaleur et température
Ne confondons pas chaleur et température.
La chaleur est un mode de transfert d'énergie interne entre des corps résultant de leur différence de température ou de leur état physique. La température $T$ d'un corps est une mesure de l'agitation thermique des particules qui le constituent : plus l'agitation thermique est importante, plus la température du corps est élevée. Elle s'exprime dans le $SI$ (système international) en Kelvin $(K).$
Autre unité : le degré Celsius $(^{\circ}C)$
La température absolue $(T)$ en kelvin $(K)$ est reliée à la température en degré Celsius $(^{\circ}C)$ par la relation :
$$T(K)=\theta (^{\circ}C)+273$$
II. Modes de transfert d'énergie par chaleur
Il s'effectue toujours du corps le plus chaud vers le corps le plus froid, jusqu'à atteindre l'équilibre thermique. Ce transfert peut se faire par :
1. Conduction thermique
La tige métallique qui a une partie plongée dans le feu de la bougie va aussi chauffer son extrémité qui n'est plongé, il y a donc propagation d'énergie thermique par chaleur d'une zone à l'autre. Une partie de l'agitation thermique des constituants de la flamme est transmise aux particules de la tige métallique qui a leur tour transmettent de proche en proche dans le métal cette agitation. C'est le phénomène de condition de l'énergie thermique
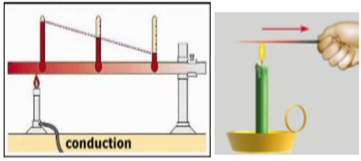
2. La convection
Sous forme de courant ascendant et descendant au sein d'un liquide. Le courant chaud monte et le froid descend formant ainsi une cellule de convection. (Le liquide chaud étant moins dense que le liquide froid).
Ce transport de matière constitue des courants de convections et l'énergie thermique s'est propager par convection

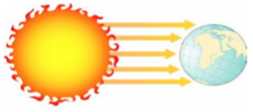
3. Le rayonnement
Les corps chauds, comme le soleil émettent des rayonnements électromagnétiques. Il se propage dans l'air et le vide et transporte de l'énergie
III. Quantité de chaleur
1. Notion de quantité de chaleur
Lorsque deux corps à des températures différentes sont mis en contact, on constate que la température du corps chaud diminue, tandis que celle du corps froid augmente. L'énergie interne du corps chaud décroît, celle du corps froid croît. Il y a transfert d'énergie entre les deux corps : c'est le transfert thermique noté $Q$ en Joule $(J).$

Convention de signe
$Q>0$, le corps ou le système reçoit de l'énergie par chaleur
$Q<0$, le corps ou le système donne de l'énergie par chaleur

L'énergie interne ou énergie thermique du corps peut avoir deux principaux effets :
$\blacktriangleright\ $L'accroissement de la température de ce corps, sans changement d'état physique
$\blacktriangleright\ $Changement d'état physique de ce corps sans variation de température
2. Chaleur échangée sans changement d'état du système
Lorsqu'un corps voit sa température varié $\theta_{i}$ (température initiale) jusqu'à $\theta_{f}$, la quantité de chaleur transférée a pour expression :
Lorsque la température d'un corps de masse $m$ passe d'une valeur initiale $\theta_{i}$ à une valeur finale $\theta_{f}$, la quantité de chaleur $Q$ échangée avec le milieu extérieur est donnée par la relation :
$$Q=mc\left(\theta_{f}-\theta_{i}\right)$$
$c$ : capacité thermique massique (ou chaleur massique) du corps en joules par kilogramme par kelvin $(J\cdot kg^{-1}K^{-1})$ ou joules par kilogramme par degré Celsus $(J\cdot kg^{-1}C^{\circ-1})$
2.1. La capacité thermique massique
La capacité massique d'un corps est la quantité de chaleur qu'il faut fournir (ou prendre) à l'unité de masse pour que sa température s'élève (ou s'abaisse) de $1$ kelvin ou de $1^{\circ}C.$
Chaleur massique de quelques corps
$$\begin{array}{|l|l|l|} \hline \text{Corps état physique}&\text{Etat physique}&C\left(J\cdot kg^{-1}\right)\\ \hline \text{Diazote}&\text{gaz}&1040\\ \hline \text{Ethanol}&\text{liquide}&2460\\ \hline \text{Zinc}&\text{solide}&417\\ \hline \text{Eau}&\text{gaz}&1850\\ \hline \text{Eau}&\text{liquide}&4186\\ \hline \text{Eau}&\text{solide}&2060\\ \hline \end{array}$$
Remarque :
$\blacktriangleright\ $Le produit $m_{C}$ s'appelle la capacité thermique ou capacité calorifique noté $C$ avec $C=m_{c}$
2.2. La capacité thermique ou capacité thermique
La capacité thermique (ou capacité calorifique) est l'énergie qu'il faut apporter à un corps pour augmenter sa température de un kelvin ou de un degré
$C$ s'exprime en joules par kelvin $\left(J/K\text{ ou }JK^{-1}\right)$ ou en joules par degrés $\left(J/C\text{ ou }JC^{-1}\right)$
La quantité de chaleur transférée s'exprime alors :
$$Q=C\left(\theta_{f}-\theta_{i}\right)$$
Remarque :
$\blacktriangleright\ $Mélange de plusieurs liquides
$c_{i}$ : capacité thermique massique de chaque liquide
$m_{i}$ : masse de chaque liquide
$\theta_{i}$ : température de chaque liquide
$C=\sum_{i=1}^{n}m_{i}C_{i}$ $(C\ :\ \text{capacité thermique du mélange})$ ;
$c=\dfrac{\sum_{i=1}^{n}m_{i}C_{i}}{\sum_{i=1}^{n}m_{i}}$ $(c\ :\ \text{capacité thermique massique du mélange})$
et $\theta=\dfrac{\sum_{i=1}^{n}m_{i}C_{i}\theta_{i}}{\sum_{i=1}^{n}m_{i}C_{i}}$ $(\theta\ :\ \text{température du mélange})$
3. Chaleur échangée avec changement d'état du système
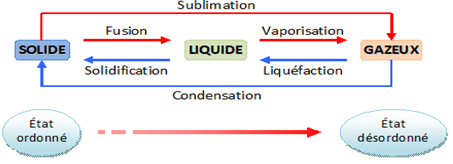
3.1. Les différents changements d'état
Un changement d'état physique correspond au passage d'un état physique à un autre état physique. Il se fait à température constante

3.2. Chaleur latente de changement d'état
Si un système échange de la chaleur avec l'extérieur, sa température peut rester constante : la chaleur sert à autre chose, par exemple à leur faire changer d'état.la chaleur mise en jeu s'appelle chaleur latente.
L'énergie thermique de changement d'état (ou chaleur latente), notée $L$, est l'énergie qu'il faut fournir à $1kg$ d'un corps pur (liquide, solide ou gaz), à sa température de changement d'état, pour qu'il change d'état.
$Q=m\cdot L$
$L>0\quad\text{ou}\quad <0.$
Exemples
Chaleur latente de fusion de l'eau glace : $L_{\text{fus}}=334\cdot10^{3} J\cdot kg^{-1}$
chaleur latente de vaporisation de l'eau liquide : $L_{\text{vap}}=2.26\cdot10^{6} J\cdot kg^{-1}$
Remarque
$\blacktriangleright\ Q$ et $L$ sont positifs pour une fusion, une vaporisation, une sublimation et négatifs pour une solidification, une liquéfaction, une condensation.
$\blacktriangleright\ L_{\text{sol}}=-L_{\text{fus}}\ ;\ L_{\text{cond}}=-L_{\text{sub}}\ ;\ L_{\text{liq}}=-L_{\text{vap}}\ ;\ $
IV. Détermination expérimentale de grandeur calorimétrique
La calorimétrie est l'étude quantitative des transferts d'énergie d'un système à l'autre à l'échelle microscopique en se basant sur la mesure des températures
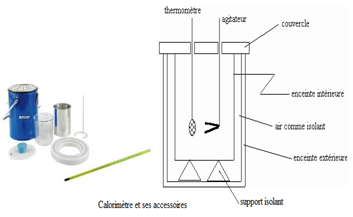
1. Le calorimètre
Le calorimètre est une enceinte adiabatique, c'est-à-dire ne permettant aucun échange de chaleur entre l'intérieur du calorimètre et l'extérieur.

Il comporte :
$\blacktriangleright\ $un vase intérieur argenté ou en aluminium brillanté ;
$\blacktriangleright\ $un vase extérieur argenté ou en aluminium pouvant contenir le vase intérieur ;
$\blacktriangleright\ $un couvercle transparent avec des ouvertures pour le thermomètre ou la sonde de température et l'agitateur
Le calorimètre et ses accessoires ont une capacité thermique
Remarque
$-\ $Le couvercle évite les phénomènes de convection dans l'air ambiant.
$-\ $Les parois argentées évitent les échanges par rayonnement (réflecteur)
$-\ $Les supports isolants, cales de liège, évitent les phénomènes de conduction
2. Bilan thermique
Lorsque plusieurs corps sont en contact dans
3.2. Méthode des mélanges
une enceinte adiabatique, ils se mettent mutuellement en équilibre thermique et la somme algébrique des quantités de chaleur échangée est nulle.
$$\sum_{i=1}^{n}Q_{i}=0$$
3. Applications
3.1. Valeur en eau du calorimètre
Le calorimètre et ces accessoires (thermomètre, agitateur...) participent aussi à l'équilibre thermique.
Quand cette participation n'est pas négligée alors on note souvent sa valeur en eau qui est une masse d'eau qui aurait la même participation thermique.
Le calorimètre et ces accessoires (thermomètre, agitateur...) participent aussi à l'équilibre thermique.
Quand cette participation n'est pas négligée alors on note souvent sa valeur en eau qui est une masse d'eau qui aurait la même participation thermique.
On plonge un corps chaud à la température $\theta_{2}$ dans un calorimètre rempli d'eau froide à la température $\theta_{1}.$ Les quantités de chaleur sont échangées sans pertes jusqu'à ce l'équilibre se fait et on mesure la température du mélange $\theta_{f}.$
\begin{eqnarray} Q_{\text{cal}}+Q_{1}+Q_{2} &=&0\nonumber\\\\\Rightarrow C\left(\theta_{f}-\theta_{1}\right)+m_{1}c_{1}\left(\theta_{f}-\theta_{1}\right)+m_{2}c_{2}\left(\theta_{f}-\theta_{2}\right) &)=& 0
\end{eqnarray}
On peut alors déduire la capacité thermique $c_{2}$ ou la température du corps introduit dans le calorimètre
Exercice d'application :
On considère un calorimètre adiabatique de masse en eau à déterminer contenant $m_{1}=0.200kg$ à la température $\theta_{1}=15^{\circ}C.$
On y ajoute $m_{2}=0.200kg$ à la température $\theta_{2}=45.9^{\circ}C.$ La température finale est $\theta_{f}=30^{\circ}C.$
Calculer la masse en eau du calorimètre.
On donne : $C_{e}=400$
Résolution
1) Calcul de la valeur en eau du calorimètre
La quantité de valeur échangée par l'eau et le calorimètre et ses accessoires
$Q_{1}=\left(\mu C_{e}+m_{1}C_{e}\right)\left(\theta_{f}-\theta_{1}\right)$
La quantité de chaleur échangée par l'eau à la température $\theta_{2}$
$Q_{2}=m_{2}C_{e}\left(\theta_{f}-\theta_{2}\right)$
Le bilan thermique s'écrit :
4. Chaleur de réaction
4.1. Définition
La chaleur de réaction est la quantité de chaleur échangée entre le système chimique et l'extérieur lors du d'une réaction chimique.
$\blacktriangleright\ $Lorsque la réaction est exothermique la chaleur de réaction est comptée conventionnellement négative : $Q$
$\blacktriangleright\ $Elle est au contraire comptée positivement lorsque la réaction est endothermique : $Q$
Exemple
4.2. Propriétés
4.2.1. Additivité
Si une réaction peut être considérée comme étant la somme des réactions, la chaleur de réaction est égale à la somme algébrique des chaleurs de réaction
Exemple
4.2.2. Principe de l'état initial et de l'état final
La chaleur de réaction réalisée sous une pression constante à une température donnée ne dépend que de l'état initial des réactifs et de l'état final des produits.
Le principe de l'état initial et de l'état final nous permet d'affirmer qu'à une température donnée, la chaleur échangée par un système lors de la réaction est l'opposée de la chaleur échangée par le système lors de la réaction inverse.

Commentaires
Anonyme (non vérifié)
dim, 03/16/2025 - 18:33
Permalien
Comment calculer la chaleur
Ajouter un commentaire