Corrigé devoir n° 2 maths - 4e

 

1) Mettons les expressions suivantes sous la forme de $2^{n}\times 3^{m}\times 5^{p}$, où $n\;,\ m$ et $p$ sont des entiers.

 

On a :

 

$\begin{array}{rcl} C&=&12\times 36\times 6^{-5}\times 100\times 5^{-3}\\\\&=&(4\times 3)\times(4\times 9)\times(2\times 3)^{-5}\times(4\times 25)\times 5^{-3}\\\\&=&2^{2}\times 3\times 2^{2}\times 3^{2}\times 2^{-5}\times 3^{-5}\times 2^{2}\times 5^{2}\times 5^{-3}\\\\&=&2^{2}\times 2^{2}\times 2^{-5}\times 2^{2}\times 3\times 3^{2}\times 3^{-5}\times 5^{2}\times 5^{-3}\\\\&=&2^{2+2-5+2}\times 3^{1+2-5}\times 5^{2-3}\\\\&=&2^{1}\times 3^{-2}\times 5^{-1}\end{array}$

 

Alors, $\boxed{C=2\times 3^{-2}\times 5^{-1}}$

 

On a :

 

$\begin{array}{rcl} D&=&2\times 64\times 6^{-5}\times 100\times 5^{-3}\\\\&=&2\times(8\times 8)\times(2\times 3)^{-5}\times(4\times 25)\times 5^{-3}\\\\&=&2\times 2^{3}\times 2^{3}\times 2^{-5}\times 3^{-5}\times 2^{2}\times 5^{2}\times 5^{-3}\\\\&=&2\times 2^{3}\times 2^{3}\times 2^{-5}\times 2^{2}\times 3^{-5}\times 5^{2}\times 5^{-3}\\\\&=&2^{1+3+3-5+2}\times 3^{-5}\times 5^{2-3}\\\\&=&2^{4}\times 3^{-5}\times 5^{-1}\end{array}$

 

Donc, $\boxed{D=2^{4}\times 3^{-5}\times 5^{-1}}$

 

2) Donnons une écriture simple de $E\ $ et $\ F.$

 

$E=\dfrac{a^{2}\times(bc^{3})^{4}}{a^{-2}\times b^{2}\times c^{2}}$

 

$F=\dfrac{n^{-3}\times(n\times m)^{3}\times n^{6}}{m^{+5}\times n^{-8}\times m^{-7}}$

 

$(a\;,\ b\;,\ c\;,\ n$ et $m$ sont différents de zéro).

 

On a :

 

$\begin{array}{rcl} E&=&\dfrac{a^{2}\times(bc^{3})^{4}}{a^{-2}\times b^{2}\times c^{2}}\\\\&=&\dfrac{a^{2}\times(b^{4}\times c^{3\times 4})}{a^{-2}\times b^{2}\times c^{2}}\\\\&=&\dfrac{a^{2}\times b^{4}\times c^{12}}{a^{-2}\times b^{2}\times c^{2}}\\\\&=&a^{2}\times b^{4}\times c^{12}\times a^{2}\times b^{-2}\times c^{-2}\\\\&=&a^{2}\times a^{2}\times b^{4}\times b^{-2}\times c^{12}\times c^{-2}\\\\&=&a^{2+2}\times b^{4-2}\times c^{12-2}\\\\&=&a^{4}\times b^{2}\times c^{10}\end{array}$

 

D'où, $\boxed{E=a^{4}\times b^{2}\times c^{10}}$

 

On a :

 

$\begin{array}{rcl} F&=&\dfrac{n^{-3}\times(n\times m)^{3}\times n^{6}}{m^{+5}\times n^{-8}\times m^{-7}}\\\\&=&\dfrac{n^{-3}\times n^{3}\times m^{3}\times n^{6}}{m^{+5}\times n^{-8}\times m^{-7}}\\\\&=&n^{-3}\times n^{3}\times m^{3}\times n^{6}\times m^{-5}\times n^{8}\times m^{7}\\\\&=&n^{-3}\times n^{3}\times n^{6}\times n^{8}\times m^{3}\times m^{-5}\times m^{7}\\\\&=&n^{-3+3+6+8}\times m^{3-5+7}\\\\&=&n^{14}\times m^{5}\end{array}$

 

Ainsi, $\boxed{F=n^{14}\times m^{5}}$

On considère l'expression suivante :
$$P(x)=3(3x-2)+(-3x+2)^{2}-12x^{2}+8x$$

1) Développons, réduisons et ordonnons $P(x)$

 

Soit :

 

$\begin{array}{rcl} P(x)&=&3(3x-2)+(-3x+2)^{2}-12x^{2}+8x\\\\&=&9x-6+((-3x)^{2}-2\times 2\times(3x)+2^{2})-12x^{2}+8x\\\\&=&9x-6+(-3)^{2}x^{2}-12x+4-12x^{2}+8x\\\\&=&9x-6+9x^{2}-12x+4-12x^{2}+8x\\\\&=&9x^{2}-12x^{2}+9x-12x+8x-6+4\\\\&=&-3x^{2}+5x-2\end{array}$

 

D'où, $\boxed{P(x)=-3x^{2}+5x-2}$

 

2) Factorisons l'expression : $P(x)$ 

 

Soit : $P(x)=3(3x-2)+(-3x+2)^{2}-12x^{2}+8x$

 

Alors,

 

$\begin{array}{rcl} P(x)&=&3(3x-2)+((-1)(3x-2))^{2}-4x(3x-2)\\\\&=&3(3x-2)+(-1)^{2}(3x-2)^{2}-4x(3x-2)\\\\&=&3(3x-2)+(3x-2)^{2}-4x(3x-2)\\\\&=&(3x-2)[3+(3x-2)-4x]\\\\&=&(3x-2)[3+3x-2-4x]\\\\&=&(3x-2)(-x+1)\end{array}$

 

D'où, $\boxed{P(x)=(3x-2)(-x+1)}$

 

3) Rangeons dans l'ordre décroissant : $P(-1)\;,\ P(0)\;,\ P(1)\ $ et $\ P\left(\dfrac{1}{2}\right)$

 

Calculons d'abord : $P(-1)\;,\ P(0)\;,\ P(1)\ $ et $\ P\left(\dfrac{1}{2}\right)$

 

Soit $P(x)=-3x^{2}+5x-2$ alors :

 

$\begin{array}{rcl} P(-1)&=&-3\times(-1)^{2}+5\times(-1)-2\\\\&=&-3-5-2\\\\&=&-10\end{array}$

 

Donc, $\boxed{P(-1)=-10}$

 

$\begin{array}{rcl} P(0)&=&-3\times 0^{2}+5\times 0-2\\\\&=&0+0-2\\\\&=&-2\end{array}$

 

Ainsi, $\boxed{P(0)=-2}$

 

$\begin{array}{rcl} P(1)&=&-3\times 1^{2}+5\times 1-2\\\\&=&-3+5-2\\\\&=&0\end{array}$

 

Donc, $\boxed{P(1)=0}$

 

$\begin{array}{rcl} P\left(\dfrac{1}{2}\right)&=&-3\times\left(\dfrac{1}{2}\right)^{2}+5\times\left(\dfrac{1}{2}\right)-2\\\\&=&-3\times\dfrac{1}{4}+\dfrac{5}{2}-2\\\\&=&-\dfrac{3}{4}+\dfrac{10}{4}-\dfrac{8}{4}\\\\&=&\dfrac{-3+10-8}{4}\\\\&=&-\dfrac{1}{4}\end{array}$

 

Alors, $\boxed{P\left(\dfrac{1}{2}\right)=-\dfrac{1}{4}}$

 

Par conséquent, dans l'ordre décroissant, on obtient :

$$P(1)>P\left(\dfrac{1}{2}\right)>P(0)>P(-1)$$

Maïmouna dispose d'un jardin potager de forme rectangulaire.

 

Elle décide d'aménager à l'intérieur un poulailler dans un espace carré de coté $x.$

 

La dimension du poulailler est égale à $\dfrac{3}{4}$ de la largeur du jardin qui est égale $\dfrac{4}{7}$ de la longueur.

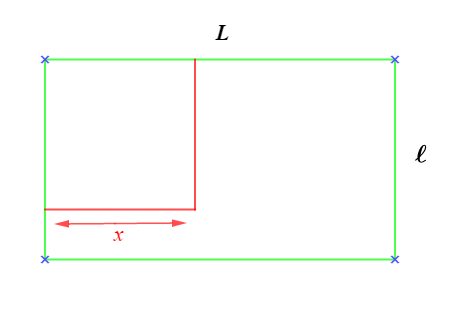
1) Calculons les dimensions du jardin.

 

On sait que la dimension du poulailler est égale à $\dfrac{3}{4}$ de la largeur du jardin.

 

Cela se traduit par : $x=\dfrac{3}{4}\ell$

 

Par suite, $4x=3\ell$

 

D'où, $\ell=\dfrac{4}{3}x$

 

Par ailleurs, la largeur du jardin est égale $\dfrac{4}{7}$ de la longueur.

 

Ce qui se traduit par : $\ell=\dfrac{4}{7}L$

 

Or, $\ell=\dfrac{4}{3}x$ donc, en remplaçant, on obtient :

 

$\begin{array}{rcl}\dfrac{4}{3}x=\dfrac{4}{7}L&\Rightarrow&3\times 4L=7\times 4x\\\\&\Rightarrow&L=\dfrac{28}{12}x\\\\&\Rightarrow&L=\dfrac{7}{3}x\end{array}$

 

Ainsi, $L=\dfrac{7}{3}x$

 

D'où, $\boxed{L=\dfrac{7}{3}x\;;\quad\ell=\dfrac{4}{3}x}$

 

2) Calculons la surface cultivable, après la mise en place du poulailler.

 

$\text{surface cultivable} = \text{surface totale du jardin} - \text{surface du poulailler}$

 

Ainsi,

 

$\begin{array}{rcl}\text{surface cultivable}&=&(L\times\ell)-(x\times x)\\\\&=&\dfrac{7}{3}x\times\dfrac{4}{3}x-x^{2}\\\\&=&\dfrac{28}{9}x^{2}-x^{2}\\\\&=&\dfrac{28}{9}x^{2}-\dfrac{9}{9}x^{2}\\\\&=&\dfrac{19}{9}x^{2}\end{array}$

 

D'où, $\boxed{\text{surface cultivable}=\dfrac{19}{9}x^{2}}$