Corrigé devoir n° 3 maths - 4e

Classe: 
Quatrième
 

Exercice 1

Sur la figure ci-dessous on a représenté la position de cinq (5) villages A, B, C, E  et  F
 
Le village E est à équidistant des villages A  et  C.
 
Le village F est à équidistant des villages B  et  C.
 
 
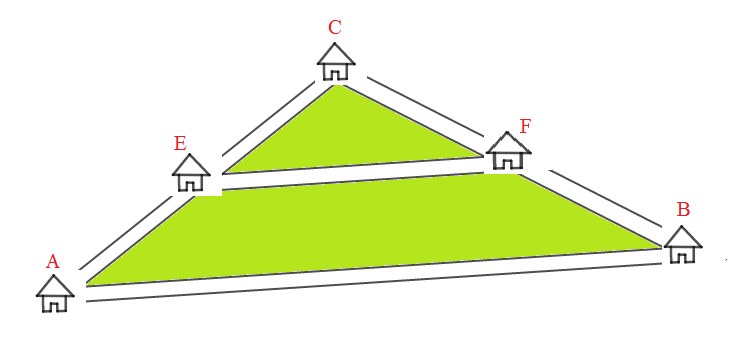
Au départ de A, Amadou a mis une demi-heure pour rejoindre le village B avec une vitesse de 2m.s−1
 
Au même moment, Badou part du village E pour rejoindre le village F, à la même vitesse.
 
1) Calculons la distance qui sépare les villages A  et  B.
 
Soit : DA↔B la la distance qui sépare les villages A  et  B.
 
Alors, on a : DA↔B=v×t avec v vitesse et t le temps mis.
 
On sait que t=30mn
 
Or, 1mn=60s donc, en convertissant le temps mis en seconde, on obtient :
 
t=30×60=1800s
 
Par suite,
 
DA↔B=2×1800=3600
 
D'où, DA↔B=3600m=3.6km
 
2) Calculons le temps mis par Badou pour rejoindre le village F.
 
On sait que : DE↔F=v×t
 
Or, DE↔F=DA↔B2
 
Donc, en remplaçant, on obtient :
 
DA↔B2=v×t⇒t=DA↔B2v⇒t=36002×2⇒t=36004⇒t=900
 
D'où, t=900s=15mn
 
Ainsi, Badou a mis un quart d'heur pour rejoindre le village F.
 
3) Énonçons la propriété géométrique utilisée.
 
Dans un triangle le segment qui joint les milieux des deux côtés quelconques a pour longueur la moitié de la longueur du troisième côté.
 
D'où, DE↔F=DA↔B2

Exercice 2

1) Développons, réduisons et ordonnons les expressions suivantes.
 
F=(5x2−9)2G=(4x9−25)(4x9+25)I=(5x3−12)2 
 
On a :
 
F=(5x2−9)2=(5x2)2−2×9×(5x2)+92=25x24−90x2+81=254x2−45x+81
 
Alors, F=254x2−45x+81
 
Soit : 
 
G=(4x9−25)(4x9+25)=(4x9)2−(25)2=16x281−425=1681x2−425
 
Donc, G=1681x2−425
 
On a : 
 
I=(5x3−12)2=(5x3)2−2×(5x3)×(12)+(12)2=25x29−10x6+14=259x2−53x+14
 
D'où, I=259x2−53x+14
 
2) Factorisons les expressions suivantes.
 
E=(4x5−17)2−(2x5+12)2F=(2x−23)2−9(32x+1)2 
 
Soit :
 
E=(4x5−17)2−(2x5+12)2=[(4x5−17)−(2x5+12)][(4x5−17)+(2x5+12)]=(4x5−17−2x5−12)(4x5−17+2x5+12)=(2x5−214−714)(6x5−214+714)=(25x−914)(65x+514)
 
Donc, E=(25x−914)(65x+514)
 
On a :
 
F=(2x−23)2−9(32x+1)2=(2x−23)2−(3(32x+1))2=[(2x−23)−3(32x+1)][(2x−23)+3(32x+1)]=(2x−23−92x−3)(2x−23+92x+3)=(42x−92x−23−93)(42x+92x−23+93)=(−52x−113)(132x+73)
 
D'où, F=(−52x−113)(132x+73)

Exercice 3

On considère les encadrements suivants :
1.20<x<1.21  et  3.90<y<3.91
1) Donnons un encadrement de xy3 à 10−2 prés.
 
En faisant le produit membre à membre des encadrements de x  et  y, on obtient :
 
1.20×3.90<xy<1.21×3.91
 
Ce qui donne : 4.68<xy<4.73
 
En divisant par 3 cet encadrement de xy, on trouve :
 
4.683<xy3<4.733
 
Par suite, 1.56<xy3<1.57
 
Comme 1.57−1.56=0.01=10−2 alors, un encadrement de xy3 à 10−2 prés est donné par :
1.56<xy3<1.57
2) Donnons un encadrement de 12x−23y à 10−2 prés.
 
En encadrant 12x, on obtient :
 
1.202<12x<1.212
 
Donc, 0.600<12x<0.605
 
Pour encadrer −23y, il faut prendre la précaution de changer le sens des inégalités.
 
On a : −3.91×23<−23y<−3.90×23
 
Par suite, −2.606<−23y<−2.600
 
En sommant membre à membre ces deux encadrements, on obtient :
 
0.600−2.606<12x−23y<0.605−2.600
 
Par suite, −2.006<12x−23y<−1.995
 
D'où, −2.00<12x−23y<−1.99
 
On a : −1.99−(−2.00)=0.01=10−2
 
Donc, un encadrement de 12x−23y à 10−2 prés sera donné par :
−2.00<12x−23y<−1.99
3) Donnons un encadrement de y−2x à 10−1 prés puis en déduisons sa valeur approchée par excès.
 
Un encadrement de y−2 est : 3.90−2<y−2<3.91−2
 
Ce qui donne : 1.90<y−2<1.91
 
On encadre ensuite 1x en changeant le sens des inégalités.
 
Ainsi, 11.21<1x<11.2
 
C'est à dire ; 0.826<1x<0.833
 
Enfin, on fait le produit membre à membre.
 
Ce qui donne : 1.90×0.826<y−2x<1.91×0.833
 
Par suite, 1.569<y−2x<1.591
 
Donc, un encadrement de y−2x à 10−1 prés est donné par :
1.5<y−2x<1.6
Ainsi, sa valeur approchée par excès est 1.6

 

Auteur: 
Diny Faye

Ajouter un commentaire