Corrigé devoir n° 4 maths - 4e

 

Mettons les expressions suivantes sous la forme de Puissances simples.

 

Soit : $A=(2\times 4\times 5)^{-3}\times((2\times 3)^{3})^{-2}\times 5^{-2}\times 2^{-2}$

 

Alors,

 

$\begin{array}{rcl} A&=&(2\times 4\times 5)^{-3}\times((2\times 3)^{3})^{-2}\times 5^{-2}\times 2^{-2}\\\\&=&(2\times 2^{2}\times 5)^{-3}\times((2\times 3)^{3})^{-2}\times 5^{-2}\times 2^{-2}\\\\&=&2^{-3}\times 2^{2\times(-3)}\times 5^{-3}\times(2^{3}\times 3^{3})^{-2}\times 5^{-2}\times 2^{-2}\\\\&=&2^{-3}\times 2^{-6}\times 5^{-3}\times 2^{3\times(-2)}\times 3^{3\times(-2)})\times 5^{-2}\times 2^{-2}\\\\&=&2^{-3}\times 2^{-6}\times 2^{-6}\times 2^{-2}\times 5^{-3}\times 5^{-2}\times 3^{-6}\\\\&=&2^{-3-6-6-2}\times 5^{-3-2}\times 3^{-6}\\\\&=&2^{-17}\times 5^{-5}\times 3^{-6}\end{array}$

 

D'où, $\boxed{A=2^{-17}\times 5^{-5}\times 3^{-6}}$

 

Soit : $B=(7^{-3}\times 2^{4})^{-2}\times(7^{3})^{-2}\times 21\times 3$

 

Alors, on a :

 

$\begin{array}{rcl} B&=&(7^{-3}\times 2^{4})^{-2}\times(7^{3})^{-2}\times 21\times 3\\\\&=&7^{(-3)\times(-2)}\times 2^{4\times(-2)}\times 7^{3\times(-2)}\times 7\times 3\times 3\\\\&=&7^{6}\times 2^{-8}\times 7^{-6}\times 7\times 3^{2}\\\\&=&7^{6}\times 7^{-6}\times 7^{1}\times 2^{-8}\times 3^{2}\\\\&=&7^{6-6+1}\times 2^{-8}\times 3^{2}\\\\&=&7^{1}\times 2^{-8}\times 3^{2}\\\\&=&7\times 2^{-8}\times 3^{2}\end{array}$

 

Ainsi, $\boxed{B=7\times 2^{-8}\times 3^{2}}$

 

Soit : $C=\dfrac{3^{-3}\times 5^{-2}\times(4^{-1})^{5}\times 3^{3}}{(5^{2})^{2}\times(4^{2}\times 3)^{3}}$

 

Alors, on a :

 

$\begin{array}{rcl} C&=&\dfrac{3^{-3}\times 5^{-2}\times(4^{-1})^{5}\times 3^{3}}{(5^{2})^{2}\times(4^{2}\times 3)^{3}}\\\\&=&\dfrac{3^{-3}\times 5^{-2}\times(2^{-2})^{5}\times 3^{3}}{(5^{2})^{2}\times(2^{4}\times 3)^{3}}\\\\&=&\dfrac{3^{-3}\times 5^{-2}\times 2^{(-2)\times 5}\times 3^{3}}{5^{2\times 2}\times 2^{4\times 3}\times 3^{3}}\\\\&=&\dfrac{3^{-3}\times 5^{-2}\times 4^{-5}\times 3^{3}}{5^{4}\times 4^{6}\times 3^{3}}\\\\&=&3^{-3}\times 5^{-2}\times 2^{-10}\times 3^{3}\times 5^{-4}\times 2^{-12}\times 3^{-3}\\\\&=&3^{-3}\times 3^{3}\times 3^{-3}\times 5^{-2}\times 5^{-4}\times 2^{-10}\times 2^{-12}\\\\&=&3^{-3+3-3}\times 5^{-2-4}\times 2^{-10-12}\\\\&=&3^{3}\times 5^{-6}\times 2^{-22}\end{array}$

 

D'où, $\boxed{C=3^{3}\times 5^{-6}\times 2^{-22}}$

 

Soit : $D=\dfrac{3^{2}\times 9^{-2}\times 0.25\times(5^{-1})^{-3}\times 7^{-3}}{(7^{2})^{-5}\times(9^{4}\times 3\times 5)^{-3}}$

 

Alors, on a :

 

$\begin{array}{rcl} D&=&\dfrac{3^{2}\times 9^{-2}\times 0.25\times(5^{-1})^{-3}\times 7^{-3}}{(7^{2})^{-5}\times(9^{4}\times 3\times 5)^{-3}}\\\\&=&\dfrac{3^{2}\times(3^{2})^{-2}\times\dfrac{1}{4}\times 5^{(-1)\times(-3)}\times 7^{-3}}{7^{2\times(-5)}\times((3^{2})^{4}\times 3\times 5)^{-3}}\\\\&=&\dfrac{3^{2}\times 3^{-4}\times 2^{-2}\times 5^{3}\times 7^{-3}}{7^{-10}\times 3^{2\times 4\times(-3)}\times 3^{-3}\times 5^{-3}}\\\\&=&\dfrac{3^{2}\times 3^{-4}\times 2^{-2}\times 5^{3}\times 7^{-3}}{7^{-10}\times 3^{-24}\times 3^{-3}\times 5^{-3}}\\\\&=&3^{2}\times 3^{-4}\times 2^{-2}\times 5^{3}\times 7^{-3}\times 7^{10}\times 3^{24}\times 3^{3}\times 5^{3}\\\\&=&3^{2}\times 3^{-4}\times 3^{3}\times 3^{24}\times 2^{-2}\times 7^{-3}\times 7^{10}\times 5^{3}\times 5^{3}\\\\&=&3^{2-4+3+24}\times 2^{-2}\times 7^{-3+10}\times 5^{3+3}\\\\&=&3^{25}\times 2^{-2}\times 7^{7}\times 5^{6}\end{array}$

 

D'où, $\boxed{D=3^{25}\times 2^{-2}\times 7^{7}\times 5^{6}}$

Soit les expressions suivantes :

 

$A=(x+2)(3x-3)-(x^{2}-4)\ $ et $\ B=(4x^{2}+16x+16)-25$

 

1) Factorisons $A\ $ et $\ B$

 

$\begin{array}{rcl} A&=&(x+2)(3x-3)-(x^{2}-4)\\\\&=&(x+2)(3x-3)-(x-2)(x+2)\\\\&=&(x+2)[(3x-3)-(x-2)]\\\\&=&(x+2)(3x-3-x+2)\\\\&=&(x+2)(2x-1)\end{array}$

 

Donc, $\boxed{A=(x+2)(2x-1)}$

 

$\begin{array}{rcl} B&=&(4x^{2}+16x+16)-25\\\\&=&(2x+4)^{2}-25\\\\&=&(2x+4)^{2}-5^{2}\\\\&=&[(2x+4)-5][(2x+4)+5]\\\\&=&(2x+4-5)(2x+4+5)\\\\&=&(2x-1)(2x+9)\end{array}$

 

Par suite, $\boxed{B=(2x-1)(2x+9)}$

 

2) Développons puis réduisons $A\ $ et $\ B$

 

$\begin{array}{rcl} A&=&(x+2)(3x-3)-(x^{2}-4)\\\\&=&3x^{2}-3x+6x-6-x^{2}+4\\\\&=&2x^{2}+3x-2\end{array}$

 

D'où, $\boxed{A=2x^{2}+3x-2}$

 

$\begin{array}{rcl} B&=&(4x^{2}+16x+16)-25\\\\&=&4x^{2}+16x+16-25\\\\&=&4x^{2}+16x-9\end{array}$

 

Donc, $\boxed{B=4x^{2}+16x-9}$

 

3) Soit $C=A+B$, factorisons $C$ puis calculons la valeur de $C$ pour $x=-\dfrac{2}{5}$

 

On a :

 

$\begin{array}{rcl} C&=&A+B\\\\&=&(x+2)(2x-1)+(2x-1)(2x+9)\\\\&=&(2x-1)[(x+2)+(2x+9)]\\\\&=&(2x-1)(x+2+2x+9)\\\\&=&(2x-1)(3x+11)\end{array}$

 

Ainsi, $\boxed{C=(2x-1)(3x+11)}$

 

Calculons $C\left(\dfrac{2}{5}\right)$

 

On a :

 

$\begin{array}{rcl} C\left(\dfrac{2}{5}\right)&=&\left(2\times\dfrac{2}{5}-1\right)\left(3\times\dfrac{2}{5}+11\right)\\\\&=&\left(2\times\dfrac{2}{5}-1\right)\left(3\times\dfrac{2}{5}+11\right)\\\\&=&\left(\dfrac{4}{5}-\dfrac{5}{5}\right)\left(\dfrac{6}{5}+\dfrac{55}{5}\right)\\\\&=&\left(-\dfrac{1}{5}\right)\left(\dfrac{61}{5}\right)\\\\&=&-\dfrac{61}{25}\end{array}$

 

D'où, $\boxed{C\left(\dfrac{2}{5}\right)=-\dfrac{61}{25}}$

 

4) Soit $D$ tel que $D-C=4x^{2}-1$

 

Donnons l'expression de $D$ puis calculons la valeur de $D$ pour $x=\dfrac{1}{2}.$

 

Soit : $D-C=4x^{2}-1$ alors, $D=4x^{2}-1+C$

 

Par suite,

 

$\begin{array}{rcl} D&=&4x^{2}-1+C\\\\&=&4x^{2}-1+(2x-1)(3x+11)\\\\&=&(2x-1)(2x+1)+(2x-1)(3x+11)\\\\&=&(2x-1)[(2x+1)+(3x+11)]\\\\&=&(2x-1)(2x+1+3x+11)\\\\&=&(2x-1)(5x+12)\end{array}$

 

D'où, $\boxed{D=(2x-1)(5x+12)}$

 

Calculons $D\left(\dfrac{1}{2}\right)$

 

On a :

 

$\begin{array}{rcl} D\left(\dfrac{1}{2}\right)&=&\left(2\times\dfrac{1}{2}-1\right)\left(5\times\dfrac{1}{2}+12\right)\\\\&=&\left(1-1\right)\left(\dfrac{5}{2}+\dfrac{24}{2}\right)\\\\&=&0\end{array}$

 

Donc, $\boxed{D\left(\dfrac{1}{2}\right)=0}$

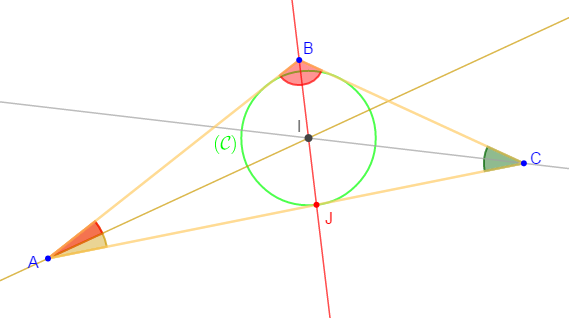
Exercice 3