Solution des exercices : Droites perpendiculaires et droites parallèles - 6e
Classe:
Sixième
Exercice 1
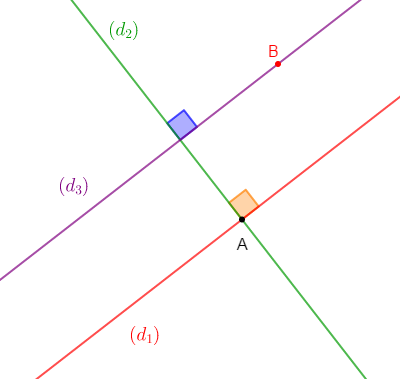
1) Traçons une droite $(d_{1})$ oblique puis marquons un point $A$ sur $(d_{1}).$
2) Traçons une droite $(d_{2})$ passant par $A$ et perpendiculaire à $(d_{1}).$
3) Marquons un point $B$ tel que $B$ n'appartenant ni à $(d_{1})$ ni à $(d_{2}).$
4) Traçons une droite $(d_{3})$ passant par $B$ et perpendiculaire à $(d_{2}).$
5) Les droites $(d_{1})\ $ et $\ (d_{3})$ sont parallèles.
Justifions la réponse par une propriété du cours.
D'après une propriété du cours, on a : si deux droites sont perpendiculaires alors, toute droite perpendiculaire à l'une est parallèle à l'autre.
Comme $(d_{2})$ est perpendiculaire à $(d_{1})\ $ et $\ (d_{3})$ perpendiculaire à $(d_{2})$ alors, en utilisant cette propriété du cours, on a : $(d_{3})$ parallèle à $(d_{1}).$
Exercice 2
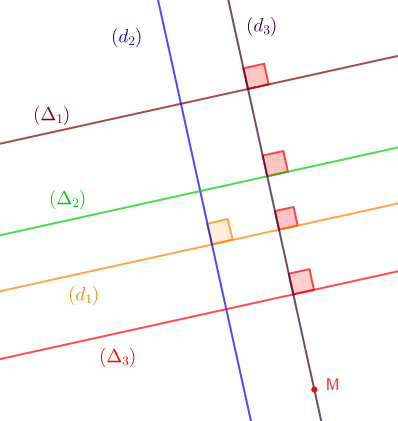
1) Traçons deux droites perpendiculaires $(d_{1})\ $ et $\ (d_{2}).$
2) Construisons trois droites $(\Delta_{1})\;,\ (\Delta_{2})\ $ et $\ (\Delta_{3})$ parallèles à $(d_{1}).$
3) Marquons un point $M$ tel que $M$ n'appartenant ni à $(d_{1})$ ni à $(d_{2}).$
4) Traçons une droite $(d_{3})$ passant par $M$ et perpendiculaire à $(d_{1}).$
5) La droite $(d_{3})$ est perpendiculaire à ces trois droites $(\Delta_{1})\;,\ (\Delta_{2})\ $ et $\ (\Delta_{3})$
Justifions
On sait que : si plusieurs droites sont parallèles entre elles alors, toute droite perpendiculaire à l'une est perpendiculaire aux autres.
Or, les trois droites $(\Delta_{1})\;,\ (\Delta_{2})\ $ et $\ (\Delta_{3})$ sont parallèles à $(d_{1}).$
Ce qui signifie que les quatre droites $(\Delta_{1})\;,\ (\Delta_{2})\;;\ (\Delta_{3})\ $ et $\ (d_{1})$ sont parallèles entre elles.
Comme $(d_{2})$ est perpendiculaire à $(d_{1})$ alors, en appliquant cette propriété, on obtient : $(d_{3})$ perpendiculaire à ces trois droites $(\Delta_{1})\;,\ (\Delta_{2})\ $ et $\ (\Delta_{3})$
Exercice 3
Répondons par vrai ou faux.
1) Si deux droites sont parallèles alors, toute droite perpendiculaire à l'une est perpendiculaire à l'autre.$\quad(\text{vrai})$
2) Si deux droites sont perpendiculaires alors toute droite perpendiculaire à l'une est perpendiculaire à l'autre.$\quad(\text{faux})$
3) Si deux droites sont parallèles alors toute droite parallèle à l'une est sécante à l'autre.$\quad(\text{faux})$
4) Si deux droites sont perpendiculaires alors toute droite perpendiculaire à l'une est parallèle à l'autre.$\quad(\text{vrai})$
Exercice 4
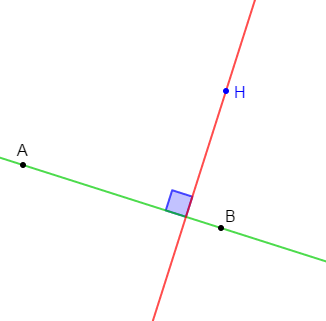
1) Marquons trois points $A\;,\ B\ $ et $\ H$ distincts du plan
2) On peut tracer une et une seule droite passant par $H$ et perpendiculaire à $(AB)$
D'après une propriété du cours, on sait que : par un point donné, il passe une et une seule droite perpendiculaire à une droite donnée.
Donc, en utilisant cette propriété, on peut dire que : par le point $H$, il passe une et une seule droite perpendiculaire à la droite $(AB).$
faisons une figure
Exercice 6 : Propriété de la médiatrice
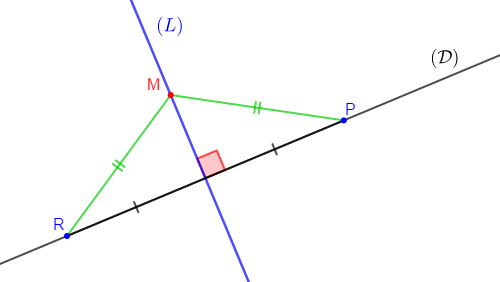
1) Marquons deux points $R\ $ et $\ P$ sur une droite $(D)$ tel que $RP=6\;cm.$
2) Construisons la droite $(L)$ médiatrice du segment $[RP].$
3) Plaçons le point $M$ sur la droite $(L)$ tel que : $RM=3.5\;cm$
4) La longueur du segment $[PM]$ est de : $3.5\;cm$
Justifions
D'après une propriété du cours, on a : tout point de la médiatrice d'un segment est à égale distance des extrémités de ce segment.
Donc, comme $(L)$ est médiatrice du segment $[RP]$ et que $M$ est sur cette médiatrice $(L)$ alors, d'après cette propriété du cours, $M$ est à égale distance de $R\ $ et $\ P.$
Ce qui signifie que $PM=RM$
Mais on sait que : $RM=3.5\;cm$
Par conséquent, $PM=3.5\;cm$
Exercice 7
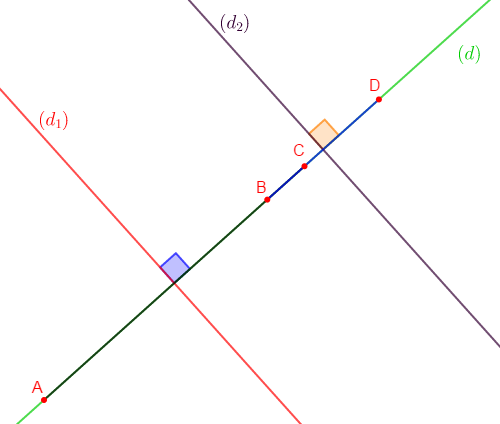
1) Sur une droite oblique $(d)$ ; marquons les points $A\;,\ B\;,\ C\ $ et $\ D$ dans cet ordre tel que : $AB=6\;cm\;;\ BC=1\;cm\ $ et $\ AD=9\;cm.$
2) Calculons les distances : $AC\;;\ BD\ $ et $\ CD.$
$-\ $ Calcul de la distance $AC$
Comme $B\in[AC]$ alors, on a :
$$AB+BC=AC$$
On remplace alors, $AB\ $ et $\ BC$ par leur valeur.
Ce qui donne : $AC=6+1=7$
D'où, $\boxed{AC=7\;cm}$
$-\ $ Calcul de la distance $BD$
Comme $B\in[AD]$ alors, on a :
$$AB+BD=AD$$
Ce qui donne :
$$BD=AD-AB$$
On remplace alors, $AD\ $ et $\ AB$ par leur valeur.
On obtient alors : $BD=9-6=3$
Ainsi, $\boxed{BD=3\;cm}$
$-\ $ Calcul de la distance $CD$
Comme $C\in[BD]$ alors, on a :
$$BC+CD=BD$$
Ce qui donne :
$$CD=BD-BC$$
On remplace alors, $BD\ $ et $\ BC$ par leur valeur.
On obtient alors : $CD=3-1=2$
D'où, $\boxed{CD=2\;cm}$
3) a) Traçons la droite $(d_{1})$ médiatrice de $[AC].$
Comme $(d_{1})$ est médiatrice de $[AC]$ alors, $(d_{1})$ est la droite qui passe par le milieu de $[AC]$ et qui est perpendiculaire au support de $[AC].$
b) Traçons la droite $(d_{2})$ médiatrice de $[BD].$
Comme $(d_{2})$ est médiatrice de $[BD]$ alors, $(d_{2})$ est la droite qui passe par le milieu de $[BD]$ et qui est perpendiculaire au support de $[BD].$
c) Les droites $(d_{1})\ $ et $\ (d_{2})$ sont parallèles.
Justifions notre réponse.
Par définition, on sait que : deux droites sont parallèles quand elles sont perpendiculaires à une même droite.
Or, les droites $(d_{1})\ $ et $\ (d_{2})$ sont perpendiculaires à la même droite $(d).$
Donc, d'après cette définition, les droites $(d_{1})\ $ et $\ (d_{2})$ sont parallèles.
Exercice 9
1) Plaçons trois points $A\;,\ I\ $ et $\ B$ alignés dans cet ordre sur une droite oblique $(d)$ tel que : $AI=3.5\;cm\ $ et $\ AB=7\;cm.$
Calculons $BI.$
Comme $I\in[AB]$ alors, on a :
$$BI+AI=AB$$
Ce qui donne :
$$BI=AB-AI$$
On remplace alors, $AB\ $ et $\ AI$ par leur valeur.
On obtient alors : $BI=7-3.5=3.5$
Donc, $\boxed{BI=3.5\;cm}$
Ainsi, on remarque que : $AI=BI=3.5\;cm$
Le point $I$ représente le milieu du segment $[AB].$
Comme les trois points $A\;,\ I\ $ et $\ B$ alignés et que $AI=BI$ alors, $I$ est milieu du segment $[AB].$
2) Traçons la droite $(d_{1})$ passant par $I$ et perpendiculaire à $(d).$
La droite $(d_{1})$ représente la médiatrice du segment $[AB].$
Justifions
Par définition, on sait que : la médiatrice d'un segment est la droite qui passe par le milieu de ce segment et qui est perpendiculaire au support de ce segment.
Or, la droite $(d_{1})$ passe par $I$ milieu du segment $[AB]$ et est perpendiculaire à la droite $(d)$ qui est le support du segment $[AB].$
Par conséquent, $(d_{1})$ est la médiatrice du segment $[AB].$
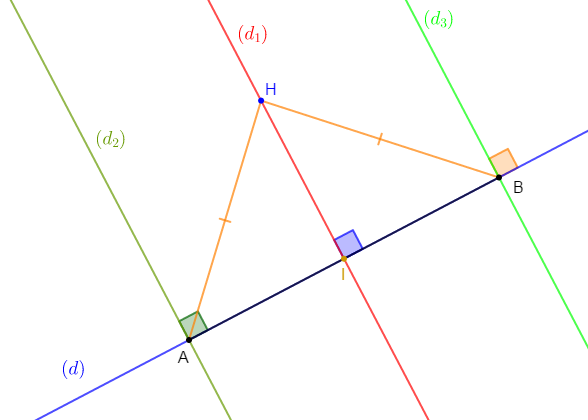
3) Marquons un point $H$ appartenant à $(d_{1})$ tel que $AH=5\;cm.$
La longueur de $[BH]$ est de : $5\;cm.$
Comme le point $H$ appartenant à $(d_{1})$ qui est médiatrice du segment $[AB]$ alors, $H$ est à égale distance de $A\ $ et $\ B.$
Ce qui signifie que : $BH=AH$
Or, $AH=5\;cm$ donc, $BH=5\;cm$
4) Traçons une droite $(d_{2})$ passant par $A$ et perpendiculaire à $(d)$ et une droite $(d_{3})$ passant par $B$ et perpendiculaire à $(d).$
Les droites $(d_{2})\ $ et $\ (d_{3})$ sont parallèles.
Justifions notre réponse.
On sait que : deux droites sont parallèles quand elles sont perpendiculaires à une même droite.
Or, les droites $(d_{2})\ $ et $\ (d_{3})$ sont perpendiculaires à la même droite $(d).$
Par conséquent, les droites $(d_{2})\ $ et $\ (d_{3})$ sont parallèles.
Exercice 10
Recopions et complétons les phrases ci-dessous par le mot qui convient.
1) La médiatrice d'un segment est la droite qui passe par le milieu de ce segment et qui est perpendiculaire au support de ce segment.
2) Deux droites sont parallèles quand elles sont perpendiculaires à une même droite.
3) Si deux droites sont parallèles alors toute droite sécante à l'une est sécante à l'autre.
4) Si un point est situé à égale distance des extrémités d'un segment alors il appartient à la médiatrice de ce segment.
Exercice 15
On considère la figure ci-dessous.
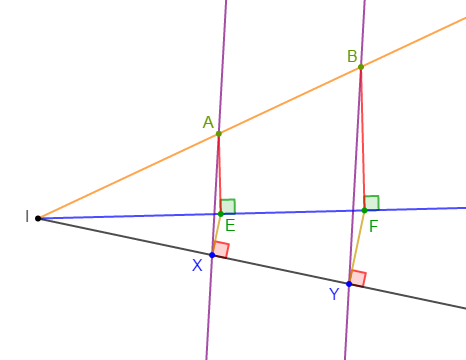
1) Reproduisons cette figure.
2) $(AE)\ $ et $\ (BF)$ sont deux droites parallèles.
Justifions notre choix.
Les droites $(AE)\ $ et $\ (BF)$ sont perpendiculaires à la même droite $(EF).$
Or, on sait que : deux droites perpendiculaires à une même droite sont parallèles.
Donc, d'après cette propriété, $(AE)\ $ et $\ (BF)$ sont deux droites parallèles.
3) Traçons les droites $(AX)\ $ et $\ (BY).$
Ces droites sont parallèles
Exercice 16
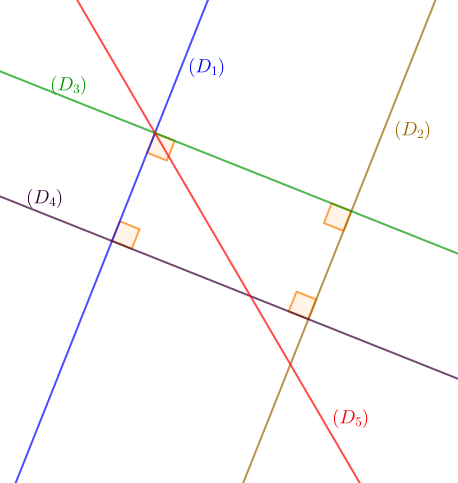
Observons la figure ci-dessous.
1) $(D_{1})\ $ et $\ (D_{3}$ sont deux droites perpendiculaires.
2) $(D_{3})\ $ et $\ (D_{4}$ sont deux droites parallèles.
Exercice 17
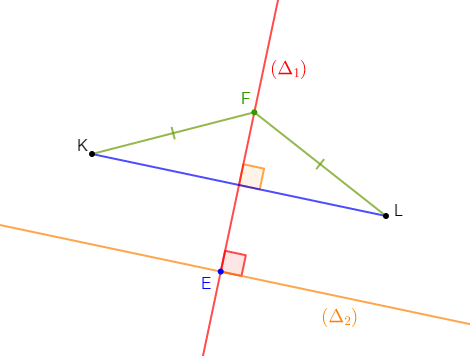
1) Traçons un segment $[KL].$
2) Construisons la droite $(\Delta_{1})$ médiatrice du segment $[KL].$
$(\Delta_{1})$ est donc la droite qui passe par le milieu de $[KL]$ et qui est perpendiculaire au support du segment $[KL].$
3) Marquons un point $E$ sur $(\Delta_{1})$ et n'appartenant pas à $[KL].$
4) Construisons la droite $(\Delta_{2})$ perpendiculaire à la droite $(\Delta_{1})$ passant par $E.$
5) Les droites $(\Delta_{2})\ $ et $\ (KL)$ sont parallèles.
Justifions notre réponse.
On a : $(\Delta_{1})$ médiatrice du segment $[KL]$ alors, $(\Delta_{1})$ est perpendiculaire à la droite $(KL).$
Aussi, $(\Delta_{2})$ est perpendiculaire à la droite $(\Delta_{1}).$
Ainsi, on a : les droites $(KL)\ $ et $\ (\Delta_{2})$ sont perpendiculaires à la même droite $(\Delta_{1}).$
Or, on sait que : deux droites perpendiculaires à une même droite sont parallèles.
D'où, en utilisant cette propriété, on a : $(\Delta_{2})$ parallèle à $(KL).$
6) Marquons un point $F$ équidistant des points $K\ $ et $\ L.$
On sait que : si tout point situé à égale distance de $K\ $ et $\ L$ appartient à la médiatrice du segment $[KL].$
Comme le point $F$ est équidistant des points $K\ $ et $\ L$ alors, il appartient à la médiatrice du segment $[KL].$
Ce qui signifie que $F$ est situé sur la médiatrice de $[KL].$
Exercice 18
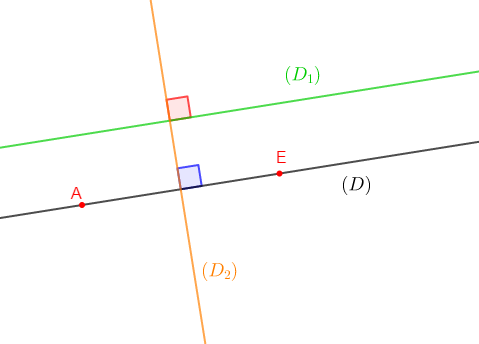
1) Plaçons sur une droite $(D)$ deux points $A\ $ et $\ E$ distincts tels que $AE=4\;cm.$
2) Construisons une droite $(D_{1})$ parallèle à $(D).$
3) Construisons la droite $(D_{2})$ médiatrice du segment $[AE].$
$(D_{2})$ est donc la droite qui passe par le milieu du segment $[AE]$ et qui est perpendiculaire à la droite $(D).$
4) Montrons que les droites $(D_{1})\ $ et $\ (D_{2})$ sont perpendiculaires.
On sait que : si deux droites sont parallèles alors, toute droite perpendiculaire à l'une est perpendiculaire à l'autre.
Or, on a : $(D_{1})$ parallèle à $(D)\ $ et $\ (D_{2})$ perpendiculaire à $(D).$
Donc, en utilisant cette propriété, on obtient : $(D_{1})$ perpendiculaire à $(D_{2}).$
Exercice 19
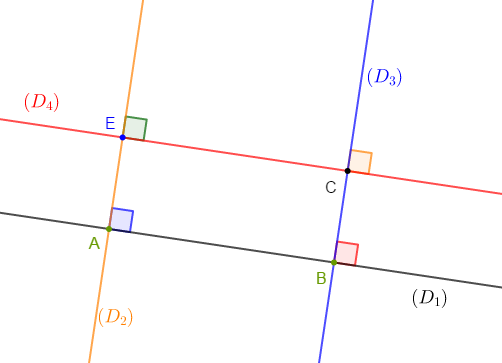
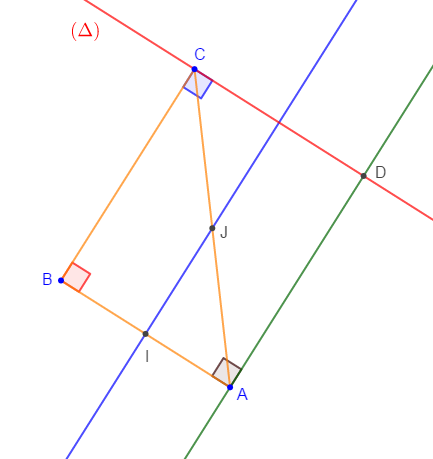
1) Construisons deux droites $(D_{1})\ $ et $\ (D_{2})$ perpendiculaires en $A.$
2) Marquons un point $B$ distinct de $A$ sur $(D_{1}).$
3) Traçons la droite $(D_{3})$ passant par $B$ et perpendiculaire à $(D_{1}).$
Les droites $(D_{2})\ $ et $\ (D_{3})$ sont parallèles.
On remarque que $(D_{2})\ $ et $\ (D_{3})$ sont deux droites qui sont perpendiculaires à une même droite $(D_{1}).$
Par conséquent, elles sont parallèles.
4) Marquons un point $C$ distinct de $B$ sur $(D_{3}).$
5) Traçons la droite $(D_{4})$ passant par $C$ et perpendiculaire à $(D_{3}).$
Les droites $(D_{4})\ $ et $\ (D_{1})$ sont parallèles.
6) Marquons le point $E$ intersection des droites $(D_{4})\ $ et $\ (D_{2}).$
7) La droite $(D_{4})$ est perpendiculaire à la droite $(D_{2})$
On sait que : si deux droites sont parallèles alors, toute droite perpendiculaire à l'une est perpendiculaire à l'autre.
Or, on a : $(D_{4})$ parallèle à $(D_{1})\ $ et $\ (D_{2})$ perpendiculaire à $(D_{1}).$
Par conséquent, la droite $(D_{2})$ est perpendiculaire à la droite $(D_{4}).$
Exercice 20
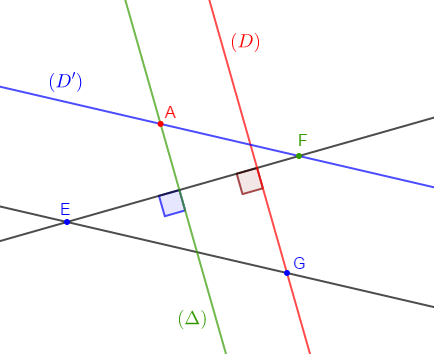
1) Traçons deux droites $(EF)\ $ et $\ (EG)$ non perpendiculaires.
2) Traçons la droite $(D)$ passant par $G$ et perpendiculaire à $(EF).$
3) Construisons la droite $(D')$ passant par $F$ et parallèle à $(EG).$
4) Marquons un point $A$ sur $(D')$ puis construisons la droite $(\Delta)$ passant par $A$ et parallèle à $(D).$
5) Les droites $(EF)\ $ et $\ (\Delta)$ sont perpendiculaires.
justifions notre réponse.
On a : $(\Delta)\ $ et $\ (D)$ sont deux droites parallèles.
On a aussi : $(EF)$ perpendiculaire à $(D).$
Or, on sait que : si deux droites sont parallèles alors, toute droite perpendiculaire à l'une est perpendiculaire à l'autre.
Donc, en utilisant cette propriété, on a bien : $(EF)$ perpendiculaire à $(\Delta).$
Exercice 23
1) Construisons un triangle $ABC$ rectangle en $B$ tel que $AB=4\;cm\ $ et $\ BC=5\;cm.$
2) Construisons les points $I\ $ et $\ J$ tels que : $I$ milieu de $[AB]\ $ et $\ J$ milieu de $[AC].$
3) On vérifie que les droites $(IJ)\ $ et $\ (BC)$ sont parallèles.
4. a) Traçons la droite $(\Delta)$ passant par $C$ et parallèle à $(AB).$
b) Les droites $(BC)\ $ et $\ (\Delta)$ sont perpendiculaires.
Justifions notre réponse.
On a : $(\Delta)$ parallèle à $(AB).$
On a aussi, $ABC$ triangle rectangle en $B.$ Ce qui signifie que $(BC)$ est perpendiculaire à $(AB).$
Or, on sait que : si deux droites sont parallèles alors, toute droite perpendiculaire à l'une est perpendiculaire à l'autre.
Donc, en utilisant cette propriété, on a : $(BC)$ perpendiculaire à $(\Delta).$
5) La perpendiculaire à $(AB)$ passant par $A$ coupe $(\Delta)$ en $D.$
a) Les droites $(AD)\ $ et $\ (BC)$ sont parallèles.
$(AD)\ $ et $\ (BC)$ sont deux droites perpendiculaires à la même droite $(AB).$
Par conséquent, elles sont parallèles.
b) Le quadrilatère $ABCD$ est un rectangle.
Justifions
On sait que : si un quadrilatère a trois angles droits alors, c'est un rectangle.
Or, on remarque que le quadrilatère $ABCD$ a trois angles droits.
Donc, en appliquant cette propriété, on peut dire que le quadrilatère $ABCD$ est un rectangle.
Exercice 24
Le maire d'une commune se propose de doter deux quartiers de la commune d'un terrain multifonctionnel pour les jeunes.
Après plusieurs rencontres entre le maire et les responsables des deux quartiers, il a été retenu de construire cette infrastructure à égale distance des deux quartiers.
Un marché est situé au milieu de ces deux quartiers distants de $900$ mètres.
Pour que le terrain multifonctionnel soit à égale distance des deux quartiers et à $500\;m$ du marché, le maire doit le placer sur une direction du marché perpendiculaire à la direction formée par les deux quartiers et à $500\;m$ du marché.
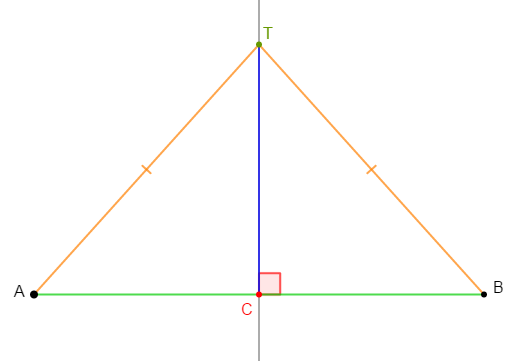
Faisons une figure à l'échelle $1/10\,000$ traduisant cette situation en notant par $A\ $ et $\ B$ les deux quartiers, $C$ le marché et $T$ le terrain.
On donne d'abord les dimensions sur la figure.
On sait que :
$$\text{Distance sur le plan}=\text{distance réelle}\times\text{échelle}$$
Donc, en remplaçant les distances réelles et l'échelle par leur valeur, on obtient les dimensions sur la figure.
Alors,
$\begin{array}{rcl} AB&=&900\times\dfrac{1}{10\,000}\\\\&=&\dfrac{900}{10\,000}\\\\&=&\dfrac{9}{100}\\\\&=&0.09\end{array}$
Ainsi, sur le plan, la distance entre les deux quartiers est donnée par :
$$AB=0.09\;m=9\;cm$$
De la même manière, on a :
$\begin{array}{rcl} TC&=&500\times\dfrac{1}{10\,000}\\\\&=&\dfrac{500}{10\,000}\\\\&=&\dfrac{5}{100}\\\\&=&0.05\end{array}$
Donc, sur le plan, la distance entre le terrain et le marché est donnée par :
$$TC=0.05\;m=5\;cm$$
Comme le terrain $T$ est à égale distance des deux quartiers $A\ $ et $\ B$ alors, $T$ est sur la médiatrice du segment $[AB].$
De plus, on sait que le marché $C$ est situé au milieu de ces deux quartiers. Cela signifie que $C$ est milieu du segment $[AB].$
Donc, on place $T$ sur la médiatrice de $[AB]$ telle que la longueur du segment $[TC]$ soit égale à : $5\;cm.$
Exercice 25
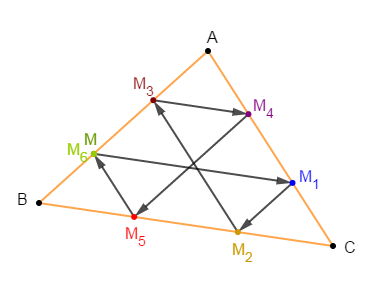
Une fourmi est placée sur une plaque triangulaire $ABC$ au point $M.$
Elle se dirige parallèlement à $(BC)$ et atteint le côté $[AC]$ en $M_{1}$, puis elle se dirige parallèlement à $(AB)$ et atteint $[BC]$ en $M_{2}$ et ainsi de suite.
1) Traçons une figure et faisons figurer les points
$$M_{1}\;,\ M_{2}\;,\ M_{3}\;,\ M_{4}\;,\ M_{5} \ \text{ et }\ M_{6}$$
2) Les droites $(MM_{1})\ $ et $\ (M_{3}M_{4})$ sont parallèles.
Justifions notre réponse.
La fourmi part de $M$ et arrive en $M_{1}$ en suivant une direction parallèle à $(BC).$ Donc, $(MM_{1})\ $ et $\ (BC)$ sont parallèles.
On a aussi : la fourmi, partant de $M_{3}$, arrive en $M_{4}$ en suivant une direction parallèle à $(BC).$ Donc, $(M_{3}M_{4})$ est parallèle à $(BC).$
Ainsi, on a : $(MM_{1})\ $ et $\ (BC)$ sont parallèles et $(M_{3}M_{4})$ est parallèle à $(BC).$
Or, on sait que : si deux droites sont parallèles alors, toute droite parallèle à l'une est parallèle à l'autre.
Donc, en utilisant cette propriété, on a : $(MM_{1})$ parallèle à $(M_{3}M_{4}).$
3) Donnons les autres droites parallèles que l'on trouve sur cette figure.
On a :
les droites $(MM_{1})\ $ et $\ (BC)$ sont parallèles
les droites $(M_{3}M_{4})\ $ et $\ (BC)$ sont parallèles
les droites $(M_{5}M_{6})\ $ et $\ (M_{2}M_{3})$ sont parallèles
les droites $(M_{5}M_{6})\ $ et $\ (AC)$ sont parallèles
les droites $(M_{2}M_{3})\ $ et $\ (AC)$ sont parallèles
les droites $(M_{4}M_{5})\ $ et $\ (AB)$ sont parallèles
les droites $(M_{1}M_{2})\ $ et $\ (M_{4}M_{5})$ sont parallèles
les droites $(M_{1}M_{2})\ $ et $\ (AB)$ sont parallèles
4) L'élève Salif affirme que sur sa figure les points $M\;,\ M_{1} \ $ et $\ M_{6}$ sont alignés.
C'est aussi le même cas sur notre figure.
On a : les points $M\ $ et $\ M_{1}$ appartiennent à la même droite $(MM_{1}).$
On remarque aussi que $M\ $ et $\ M_{6}$ sont confondus. Ce qui signifie $M=M_{6}.$
Donc, le point $M_{6}$ appartient aussi à la droite $(MM_{1}).$
Ainsi, les points $M\;;\ M_{1}\ $ et $\ M_{6}$ appartiennent à la même droite $(MM_{1}).$
Par conséquent, ils sont alignés.
Exercice 26
Deux villes $A\ $ et $\ B$ sont distantes de $10\;km.$
Une troisième ville $C$ se trouve à $5\;km$ de la ville $A$ dans une direction perpendiculaire à celle formée par les villes $A\ $ et $\ B.$
Un centre d'élevage $E$ se trouve au milieu des villes $B\ $ et $\ C.$
Une route menant au centre d'élevage et de direction parallèle à celle des villes $A\ $ et $\ C$ est construite.
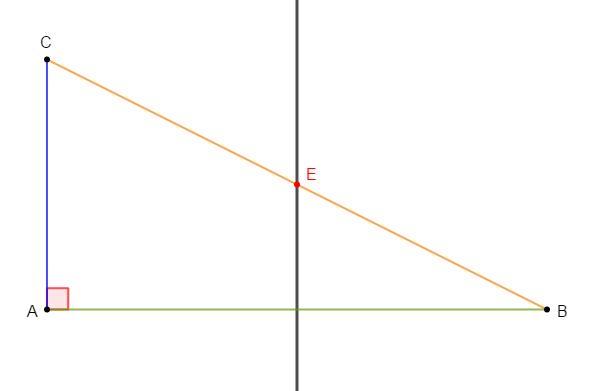
Construisons une figure géométrique décrivant cette situation.
On donne d'abord les dimensions sur la figure.
D'après l'échelle, on a : $1\;cm$ représente $1\;km$
Comme les deux villes $A\ $ et $\ B$ sont distantes de $10\;km$ alors, sur la figure, $10\;cm$ vont représenter $10\;km.$
Donc, on a : $AB=10\;cm$
Aussi, comme la ville $C$ se trouve à $5\;km$ de la ville $A$ alors, sur la figure, $5\;cm$ vont représenter $5\;km.$
Ainsi, on a : $AC=5\;cm$
Ensuite, on sait que la ville $C$ se trouve à $5\;km$ de la ville $A$ dans une direction perpendiculaire à celle formée par les villes $A\ $ et $\ B.$
Cela signifie que les droites $(AB)\ $ et $\ (AC)$ sont perpendiculaires en $A.$
Comme le centre d'élevage $E$ se trouve au milieu des villes $B\ $ et $\ C$ alors, on a : $E$ est le milieu du segment $[BC].$
Enfin, la route menant au centre d'élevage est représentée par la droite passant par $E$ et parallèle à la droite $(AC)$
Auteur:
Diny Faye

Commentaires
Anonyme (non vérifié)
jeu, 02/16/2023 - 15:17
Permalien
Très bien
Anonyme (non vérifié)
lun, 08/12/2024 - 16:38
Permalien
merci
Ajouter un commentaire