Solutions des exercices : Loi de Laplace - Ts
Classe:
Terminale
Exercice 1
1) Sens d'inclinaison de la tige $AN.$ (Voir figure)
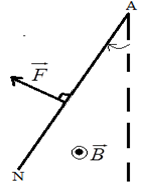
2) a) Caractéristiques de la force de la place $\overrightarrow{F}$ qui agit sur la tige $AN$
Direction ; point d'application $($milieu de la tige $AN)$ ; sens : (voir figure)
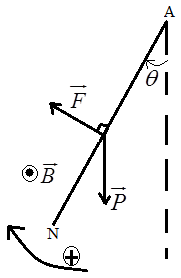
Intensité :
$\begin{array}{rcl} F&=&I_{2}IB_{1} \\ \\&=&5\times 4\cdot 10^{-2}\times 0.3\\ \\\Rightarrow F&=&-2 0.06N \end{array}$
b) Représentation de $\overrightarrow{F}$ (voir figure)
c) Détermination de la masse de la tige $AN$
La tige $AN$ est soumise aux forces : $\overrightarrow{F}$ ; $\overrightarrow{P}$ ; $\overrightarrow{R}$
La condition d'équilibre s'écrit :
$\begin{array}{rcl} M_{A}\left(\overrightarrow{P}\right)+M_{A}\left(\overrightarrow{F}\right)+M_{A}\left(\overrightarrow{R}\right)&=&\vec{0} \\ \\\Rightarrow\,-mg\dfrac{L\sin\theta}{2}+I_{2}lB_{1}\dfrac{L}{2}+0&=& 0\\ \\\Rightarrow m&=&\dfrac{I_{2}IB_{1}}{g\sin\theta}\\\\&=&\dfrac{5\times 4\cdot 10^{-2}\times 0.3}{10\sin 10^{\circ}}\\\\\Rightarrow\,m&=&0.035Kg \end{array}$
3) a) Il y a une interaction entre les deux tiges
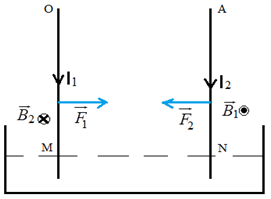
La tige $OM$ parcouru un courant $I_{1}$ crée au voisinage un champ magnétique $\overrightarrow{B_{1}}$ de la tige $AN$ qui, à son tour parcourue par $I_{2}$, subit une force
La tige $AN$ parcouru un courant $I_{2}$ crée au voisinage un champ magnétique $\overrightarrow{B_{2}}$ de la tige $OM$ qui, à son tour parcourue par $I_{1}$, subit une force $\overrightarrow{F_{1}}$
b) $I_{1}$ s'agit d'une interaction attractive.
c) La tige $OM$ est inclinée vers la tige $AN.$
d) Détermination de la valeur du champ $\overrightarrow{B_{2}}$
$B_{2}=\dfrac{\mu_{0}I}{2\pi MN}$
Exercice 2
1) Représentation des forces exercées sur le fil.
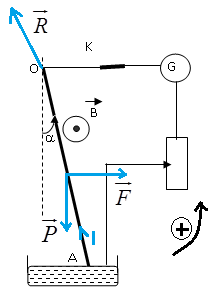
2) Sens du courant électrique. (Voir figure)
3) Calcul de l'angle $\alpha$
La condition d'équilibre appliquée à la tige s'écrit :
$\begin{array}{rcl} M_{O}\left(\overrightarrow{P}\right)+M_{O}\left(\overrightarrow{F}\right)+M_{O}\left(\overrightarrow{R}\right)&=&0 \\\\\Rightarrow\,-mg\dfrac{l\sin\alpha}{2}+IlB\dfrac{l}{2}+0&=& 0\\ \\\Rightarrow\sin\alpha&=&\dfrac{IlB}{mg}\\\\&=&\dfrac{5\times 25\cdot 10^{-2}\times 0.05}{10\times 8\cdot 10^{-3}}\\\\\Rightarrow\sin\alpha&=&0.78\\ \\ \alpha&=&51^{\circ} \end{array}$
Exercice 3
1) Tracé de la courbe $m=f(I).$
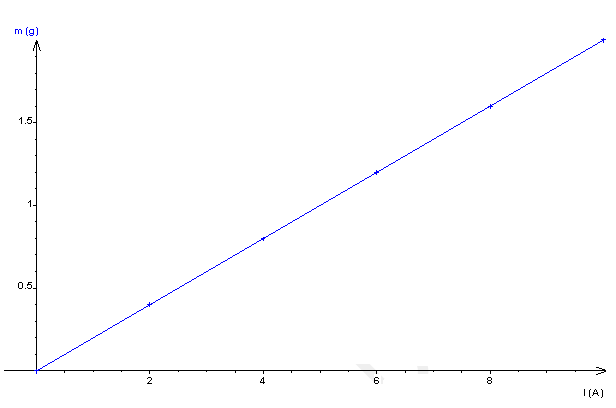
2) Établissement de la relation théorique $m=f(I).$
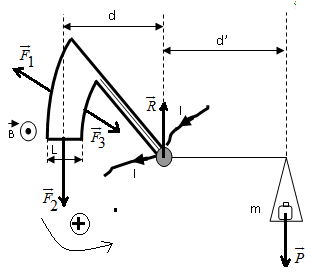
La balance est soumise aux forces : $\overrightarrow{F_{1}}$ ; $\overrightarrow{F_{2}}$ ; $\overrightarrow{F_{3}}$ ; $\overrightarrow{P}$ et $\overrightarrow{R}$
$\begin{array}{rcl} M_{\Delta}\left(\overrightarrow{P}\right)+M_{\Delta}\left(\overrightarrow{F_{1}}\right)+M_{\Delta}\left(\overrightarrow{F_{2}}\right)+M_{\Delta}\left(\overrightarrow{F_{3}}\right)+M_{\Delta}\left(\overrightarrow{R}\right)&=&0 \\ \\\Rightarrow\,-mgd'+0+ILBd+0+0&=& 0\\ \\\Rightarrow\,m&=&\dfrac{ILBd}{gd'} \end{array}$
3) Valeur du champ magnétique
Le graphe est une droite qui passe par l’origine de pente positive
$m=\dfrac{ILBd}{gd'}$
or $d'=\dfrac{5}{4}d$
$\Rightarrow\,m=\dfrac{4LB}{5g}I$
$\begin{array}{rcl} \Rightarrow\dfrac{4LB}{5g}&=&\dfrac{\Delta m}{\Delta I}\\ \\\Rightarrow\,B&=&\dfrac{5g\Delta m}{4L\Delta I}\\ \\&=&\dfrac{5\times 10\left(1\cdot 10^{-3}-0\right)}{4\times 2\cdot 10^{-2}(5-0)}\\ \\\Rightarrow\,B&=&0.125T \end{array}$
3) La masse maximale supportable par la balance
$\begin{array}{rcl} m&=&\dfrac{4\times2\cdot 10^{-2}\times 0.125}{5\times 10}\times 12\\\\\Rightarrow\,m&=&2.4g \end{array}$
La masse maximale supportable par la balance est inférieure $m=2.45g$ ; donc la balance ne peut pas supporter une telle masse.
Exercice 4
1) Représentation des forces qui exercent sur la barre $\overrightarrow{P}.$
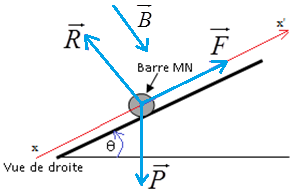
Sens de $\overrightarrow{B}$ (voir schéma)
a) La condition la condition d'équilibre de la barre $MN$ s'écrit :
$\overrightarrow{P}+\overrightarrow{F}+\overrightarrow{R}=\vec{0}$
b) Expression de la norme de $B$ en fonction de $I_{1}$, $L$, $m$, $g$ et $\theta.$
Pour que la barre reste en équilibre.
$\overrightarrow{P}+\overrightarrow{F}+\overrightarrow{R}=\vec{0}$
En projetant la relation suivant l'axe $xx'$
$\begin{array}{rcl} -mg\sin\theta+I_{1}LB+0&=&0\\\\\Rightarrow\,B&=&\dfrac{mg\sin\theta}{I_{1}L} \end{array}$
Montrons que $B=68mT.$
$\begin{array}{rcl} B&=&\dfrac{mg\sin\theta}{I_{1}L}\\\\&=&\dfrac{10\cdot 10^{-3}\times 10\times\sin 20^{\circ}}{10\times 0.05}\\\\\Rightarrow\,B&=&68mT \end{array}$
3) a) Représentation des forces qui exercent sur la barre $MN.$
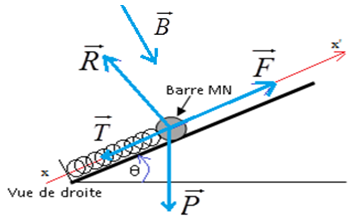
b) La condition d'équilibre de la barre s'écrit :
$\overrightarrow{P}+\overrightarrow{F}+\overrightarrow{R}+\overrightarrow{T}=\vec{0}$
Valeur de la constante de raideur $k$ du ressort.
En projetant la relation suivant l'axe $xx'$
$\begin{array}{rcl} -mg\sin\theta+I_{1}LB+0-k\Delta l&=&0\\\\\Rightarrow\,k&=&\dfrac{I_{2}LB-mg\sin\theta}{\Delta l}\\\\k&=&\dfrac{15\times 0.05\times 68\cdot 10^{-3}-10\cdot 10^{-3}\times 10\times\sin 20^{\circ}}{3.6\cdot 10^{-3}}\\\\\Rightarrow\,k&=&4.7N\cdot m^{-1} \end{array}$
Exercice 5
1) a) Sens du courant traversant la tige. Voir figure
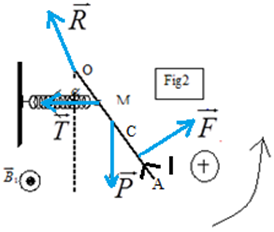
b) Caractéristiques de la force de la place exercée sur la tige
$\bullet\ $Point d'application : milieu $AC$
$\bullet\ $Direction : perpendiculaire à la tige
$\bullet\ $Sens : voir figure
$\bullet\ $Intensité :
$\begin{array}{rcl} F&=&I_{1}lB_{1}\\\\&=&10\times 10\cdot 10^{-2}\times 0.1\\\\\Rightarrow\,F&=&0.1N \end{array}$
2) a) Bilan des forces qui exercent sur la tige : $\overrightarrow{P}$ ; $\overrightarrow{F}$ ; $\overrightarrow{R}$ et $\overrightarrow{T}$
b) Détermination de l'allongement du ressort $\Delta l.$
Le théorème des moments appliqué à la tige s'écrit :
$\begin{array}{rcl} M_{O}\left(\overrightarrow{P}\right)+M_{O}\left(\overrightarrow{F}\right)+M_{O}\left(\overrightarrow{T}\right)+M_{O}\left(\overrightarrow{R}\right)&=&0\\\\\Rightarrow -mg\dfrac{L}{2}\sin\alpha+I_{1}lB_{1}\left(L-\dfrac{l}{2}\right)+0-k\Delta ll\cos\alpha&=&0\\\\\Delta l&=&\dfrac{I_{1}lB_{1}\left(L-\dfrac{l}{2}-mg\dfrac{L}{2}\sin\alpha}{kl\cos\alpha}\\\\&=&\dfrac{10\times 10\cdot 10^{-2}\times 0.1\left(40\cdot 10^{-2}-5\cdot 10^{-2}\right)-10\cdot 10^{-3}\times 10\times 20\cdot 10^{-2}\times\sin 8^{\circ}}{23\times 10\cdot 10^{-2}\times\cos 8^{\circ}}\\ \\\Rightarrow\Delta l&=&0.014m \end{array}$
3) a) Bilan des forces qui exercent sur la tige : $\overrightarrow{P}$ ; $\overrightarrow{F}$ et $\overrightarrow{R}$
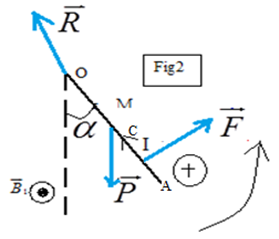
b) Détermination de la valeur du champ magnétique $\overrightarrow{B_{2}}.$
$\begin{array}{rcl} M_{O}\left(\overrightarrow{P}\right)+M_{O}\left(\overrightarrow{F}\right)+M_{O}\left(\overrightarrow{R}\right)&=&0\\\\\Rightarrow-mg\dfrac{L}{2}\sin\alpha+I_{1}l\left(B_{1}-B_{2}\right)\left(L-\dfrac{1}{2}\right)+0&=&0\\\\\Rightarrow\,B_{2}&=&B_{1}-\dfrac{mg\dfrac{L}{2}\sin\alpha}{I_{1}l\left(L-\dfrac{l}{2}\right)}\\\\&=&0.1-\dfrac{10\cdot 10^{-3}\times 10\times 20\cdot 10^{-2}\times\sin 4^{\circ}}{10\times 10\cdot 10^{-2}\times\left(40\cdot 10^{-2}-5\cdot 10^{-2}\right)}\\\\\Rightarrow\,B_{2}&=&0.096T \end{array}$
4) a) Caractéristiques de la force de Laplace
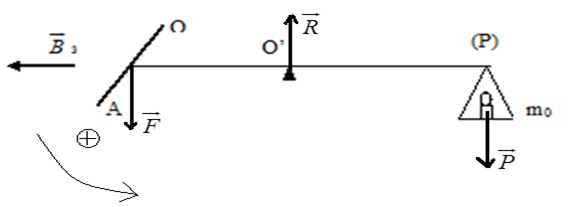
$\bullet\ $Point d'application : milieu $AC$
$\bullet\ $Direction : la verticale
$\bullet\ $Sens : de haut en bas
$\bullet\ $Intensité : $F=I_{3}lB_{3}$
b) Le courant $I_{3}$ circule de $O$ vers $A$
Calcul de la valeur de $I_{3}$
$\begin{array}{rcl} M_{O'}\left(\overrightarrow{P}\right)+M_{O'}\left(\overrightarrow{F}\right)+M_{O'}\left(\overrightarrow{R}\right)&=&0\\\\\Rightarrow-m_{0}gO'P+I_{3}lB_{3}O'A+0&=&0\\\\(O'P=O'A)\Rightarrow-m_{0}gO'P+I_{3}lB_{3}O'A+0&=&0\\\\\Rightarrow\,I_{3}&=&\dfrac{m_{0}g}{lB_{3}}\\\\&=&\dfrac{4\cdot 10^{-3}\times 10}{10\cdot 10^{-2}\times 5\cdot 10^{-2}}\\\\\Rightarrow\,I_{3}&=&4A \end{array}$
Exercice 6
1) a) Représentation des forces qui s'exercent sur la tige $(T)$
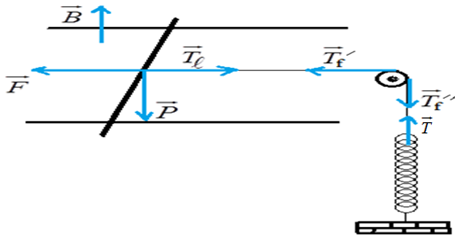
b) L'allongement du ressort est dû à la force à la tension du fil de direction verticale et de sens ascendant.
c) Le champ magnétique $\overrightarrow{B}$ est de direction verticale et de sens ascendant. Ce champ est dirigé suivant l'axe nord-sud.
2) a) Montrons que l'équation de la courbe est de la forme : $I=ax$
Système étudié : la tige
Référentiel d'étude : terrestre supposé galiléen
Bilan des forces appliquées :
$\overrightarrow{P}=m\overrightarrow{g}$ ; $\overrightarrow{T_{f}}$ ; $\overrightarrow{R}$
$\overrightarrow{F}=i\overrightarrow{L}\wedge\overrightarrow{B}$
La condition d'équilibre s'écrit :
$\overrightarrow{P}+\overrightarrow{F}+\overrightarrow{R}+\overrightarrow{T_{f}}=\vec{0}$
En projetant la relation suivant $\overrightarrow{F}$ force de Laplace
$0+0-T_{f}+F=0$ ; $F=ILB$
Le fil est inextensible et le poids de la poulie est négligeable :
$\begin{array}{rcl} T_{f}&=&T\\\\&=&kx\\\\\Rightarrow-kx+ILB&=&0\\\\\Rightarrow\,ILB&=&kx\\\\\Rightarrow\,I&=&\dfrac{k}{LB}x\\\\&=&ax\\\\\Rightarrow\,a&=&\dfrac{k}{LB} \end{array} $
b) Le graphe représentant $I$ en fonction de $x$ est une droite dont sa pente ou son coefficient directeur est a :
$\begin{array}{rcl} a&=&\dfrac{\Delta I}{\Delta x}\\\\&=&\dfrac{5-0}{2.5\cdot 10^{-3}-0}\\\\\Rightarrow\,a&=&2\cdot 10^{3}A\cdot m^{-1} \end{array}$
c) Relation qui lie $B$, $I$, $k$, $x$ et $L$
$I=\dfrac{k}{LB}x=ax$
$\begin{array}{rcl} a&=&\dfrac{k}{LB}\\\\\Rightarrow\,B&=&\dfrac{k}{aL}\\\\&=&\dfrac{10}{2\cdot 10^{3}\times 10\cdot 10^{-2}}\\\\\Rightarrow\,B&=&0.05T \end{array}$
3) a) Représentation des forces qui s'exercent sur la tige.
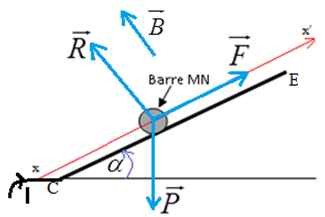
b) Montrons que la masse $m$ de la tige $(T)$ est donnée par l'expression : $m=\dfrac{IBL}{g\sin\alpha}$
Le système est en équilibre, la condition d'équilibre s'écrit :
$\overrightarrow{P}+\overrightarrow{F}+\overrightarrow{R}=\vec{0}$
La projection de la relation suivant $CE$ :
$\begin{array}{rcl} -mg\sin\alpha+ILB+0&=&0\\\\\Rightarrow\,mg\sin\alpha&=&ILB\\\\\Rightarrow\,m&=&\dfrac{ILB}{g\sin\alpha} \end{array}$
c) Calcul de la valeur de la masse $m$
$\begin{array}{rcl} m&=&\dfrac{ILB}{g\sin\alpha}\\\\&=&\dfrac{1\times 10\cdot 10^{-2}\times 0.05}{9.8\times\sin 15^{\circ}}\\\\\Rightarrow\,m&=&1.97\cdot 10^{-3}Kg \end{array}$

Commentaires
Papa Saloum (non vérifié)
mer, 04/26/2023 - 23:58
Permalien
Études
Papa Saloum (non vérifié)
mer, 04/26/2023 - 23:58
Permalien
Études
Ajouter un commentaire