Solutions des exercices : Induction Magnétique - Étude d'un dipôle RL - Ts
Classe:
Terminale
Exercice 1
I
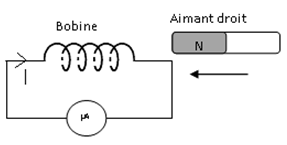
1) Le phénomène observé est l'induction électromagnétique
2) Le sens de circulation du courant induit dans la bobine. (Voir schéma)
3) L'inducteur, source du champ magnétique, est l'aimant droit.
L'induit, siège du courant induit, est la bobine.
II
1) a) Montrons que la bobine est le siège d'un phénomène d'auto-induction
Le circuit est le siège d'un courant d'intensité variable. Le courant crée, en tout point de la bobine, un champ magnétique variable à travers le circuit lui-même. Cette variation s'accompagne d'une f.é.m. ou d'un courant d'un courant d'auto-induction.
b) Montrons que la tension aux bornes de la bobine est : $u_{AB}=\dfrac{-L}{R}\dfrac{\mathrm{d}u_{CB}}{\mathrm{d}t}$
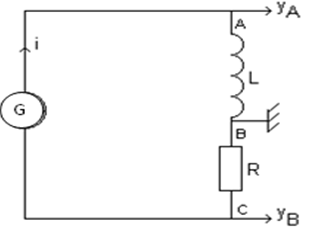
$u_{AB}=L\dfrac{\mathrm{d}i}{\mathrm{d}t}$
$\begin{array}{rcl} u_{CB}&=&-Ri\\\\\Rightarrow\,i&=&-\dfrac{u_{CB}}{R}\\\\\Rightarrow\,u_{AB}&=&L\dfrac{\mathrm{d}\left(-\dfrac{u_{CB}}{R}\right)}{\mathrm{d}t}\\\\\Rightarrow\,u_{AB}&=&-\dfrac{L}{R}\dfrac{\mathrm{d}u_{CB}}{\mathrm{d}t} \end{array}$
c) Justifions littéralement l'allure de la tension sur la voie $Y_{A}$
La tension aux bornes résistor est triangulaire de la forme : $u_{CB}=at+b$
$\dfrac{\mathrm{d}u_{CB}}{\mathrm{d}t}=a\Rightarrow\,u_{AB}=-\dfrac{L}{R}a$
La bobine transforme une tension triangulaire en tension carrée ; d'où l'allure de la tension sur la voie $Y_{A}$
2) a) Calcul de la période $T$ et la de fréquence $N$ des tensions
$T=0.2\cdot 10^{-3}\times 8\Rightarrow\,T=1.6\cdot 10^{-3}s$
$N=\dfrac{1}{1.6\cdot 10^{-3}}$
$\Rightarrow\,N=625Hz$
b) Détermination des expressions de $u_{AB}$ et de $u_{CB}$ en fonction du temps.
$\begin{array}{rcl} u_{AB}&=&1\times 0.2\\\\\Rightarrow\,u_{AB}&=&0.2V \end{array} $
$\begin{array}{rcl} u_{CB}&=&2\times 2\\\\\Rightarrow\,u_{CB}&=&4V \end{array} $
c) Valeur de l'inductance $L$ de la bobine
$\begin{array}{rcl} u_{AB}&=&-\dfrac{L}{R}\dfrac{\mathrm{d}u_{CB}}{\mathrm{d}t}\\\\\Rightarrow\,L&=&-Ru_{AB}\dfrac{\mathrm{d}t}{\mathrm{d}u_{CB}}\\\\&=&-10\cdot 10^{3}\times 0.2\times\left(\dfrac{0.8\cdot 10^{-3}}{-4}\right)\\\\\Rightarrow\,L&=&0.4H \end{array}$
Signification physique de l'inductance :
L'inductance est une grandeur physique caractérisant l'aptitude d'une bobine à modérer les variations de tout courant électrique qui y circule.
Exercice 2
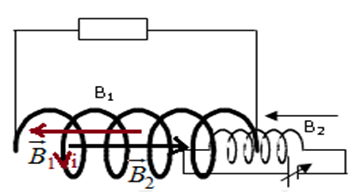
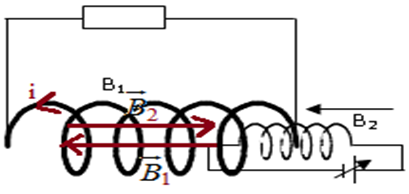
1) a) Représentation du champ magnétique créé par la bobine $B_{2}.$ (voir figure)
b) Énoncé la loi de Lenz.
Toute variation de flux à travers un circuit fermé entraine la circulation d'un courant induit qui, par ses effets électromagnétiques, s'oppose à la cause qui lui a donné naissance.
Représentation du champ magnétique induit dans la bobine $B_{1}.$ (voir figure)
Le sens du courant induit. (voir figure)
c) La bobine $B_{2}$ est l'inducteur et $B_{1}$ l'induit
2) a) En diminuant l'intensité du courant débitée par le générateur la valeur du champ magnétique créé par la bobine $B_{2}$ diminue.
b) Représentation du champ magnétique créé par $B_{2}$ et de celui qui est induit dans $B_{1}.$
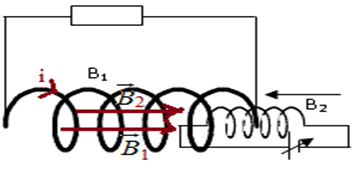
c) Sens du courant induit dans $B_{1}.$ (voir figure)
3) Représentation du champ magnétique induit dans la bobine $B_{1}$ lorsque on modifie les bornes générateur
Exercice 3
1) Schéma de principe du montage
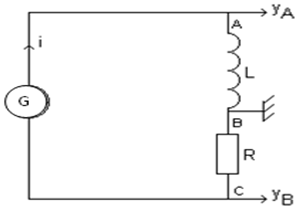
2) La tension aux bornes de la résistance permet d'observer l'allure de $i(t)$ car cette tension est proportionnelle à l'intensité du courant électrique. A une constante $R$ près, la voie $Y_{B}$ visualise les variations de l'intensité.
3) Détermination de la période $T$ de l'intensité du courant
$T=4\times 0.5\cdot 10^{-3}\Rightarrow\,R=2\cdot 10^{-3}s$
4) Détermination de l'amplitude $I_{m}$ (valeur maximale atteinte) de l'intensité du courant
$\begin{array}{rcl} u_{CB}&=&RI_{m}\\\\\Rightarrow\,I_{m}&=&\dfrac{u_{CB}}{R}\\\\&=&\dfrac{2\times 4}{10\cdot 10^{3}}\\\\\Rightarrow\,I_{m}&=&80\cdot 10^{-3}A \end{array}$
5) a) Détermination de la valeur de la tension $u_{L}$
$u_{L}=3\times 0.1\Rightarrow\,u_{L}=0.3V$
b) Détermination de la valeur de la dérivée par rapport au temps de l'intensité du courant
$\begin{array}{rcl} u_{CB}&=&-Ri\\\\\Rightarrow\,i&=&-\dfrac{u_{CB}}{R}\\\\\Rightarrow\dfrac{\mathrm{d}i}{\mathrm{d}t}&=&-\dfrac{1}{R}\dfrac{\mathrm{d}u_{CB}}{\mathrm{d}t}\\\\&=&-\dfrac{1}{10\cdot 10^{3}}\dfrac{(-4-4)}{10^{-3}}\\\\\Rightarrow\dfrac{\mathrm{d}i}{\mathrm{d}t}&=&0.8A\cdot s^{-1} \end{array}$
c) Valeur de $L$ de l'inductance de la bobine.
$\begin{array}{rcl} u_{L}&=&L\dfrac{\mathrm{d}i}{\mathrm{d}t}\\\\\Rightarrow\,L&=&u_{L}\dfrac{\mathrm{d}t}{\mathrm{d}i}\\\\&=&0.3\times\dfrac{l}{0.8}\\\\\Rightarrow\,L&=&0.4H \end{array}$
Exercice 4
1) Détermination de la direction et le sens du vecteur champ magnétique. ( Voir figure)
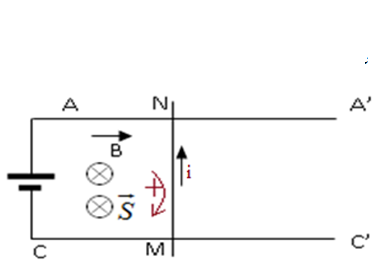
2) a) Sens positif et tracé du vecteur surface $\overrightarrow{S}.$
b) Détermination de l'expression du flux magnétique à travers le circuit.
$\Phi=\overrightarrow{B}\cdot\overrightarrow{S}=BS\cos\left(\overrightarrow{B}\cdot\overrightarrow{S}\right)$
or $\cos\left(\overrightarrow{B}\cdot\overrightarrow{S}\right)=\cos 0=0$
$\Rightarrow\Phi=BS$
Montrons que ce flux s'écrit sous la forme : $\Phi=B\cdot L\cdot V\cdot t$
$\Phi=BS$
or $S=MN\times CM=L\times Vt$
$\Rightarrow\Phi=BLVt$
3) a) Calcul de la force électromotrice induite
$\begin{array}{rcl} e&=&-\dfrac{\mathrm{d}\Phi}{\mathrm{d}t}\\\\\text{or}\quad\Phi&=&BLVt\\\\\Rightarrow\,e&=&-BLV\\\\&=&-1\times 25\cdot 10^{-2}\times 10\\\\\Rightarrow\,e&=&-0.25V \end{array}$
b) Calcul de l'intensité $i$ du courant induit
$\begin{array}{rcl} e&=&ri\\\\\Rightarrow\,i&=&\dfrac{e}{r}\\\\&=&\dfrac{-0.25}{0.5}\\\\\Rightarrow\,i&=&*-0.25A \end{array}$
c) Détermination du sens du courant induit.
Le sens du courant induit est de sens contraire du sens positif
d) Représentation de $i$ sur le schéma. (voir figure)
Exercice 5
1) a) Établissement de l'expression de l'inductance $L$ du solénoïde.
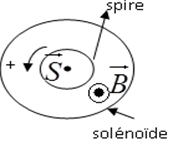
$\begin{array}{rcl} \Phi&=&N\overrightarrow{B}\cdot\overrightarrow{S}\\\\&=&N\overrightarrow{B}\cdot S\vec{n}\\\\&=&NBs\\\\&=&\dfrac{\mu_{0}N^{2}S}{l}i\\\\&=&Li\\\\\Rightarrow\,L&=&\dfrac{\mu_{0}N^{2}S}{l} \end{array}$
Calcul de la valeur de l'inductance
$\begin{array}{rcl} L&=&\dfrac{\mu_{0}N^{2}S}{l}\\\\&=&\dfrac{\mu_{0}N^{2}\pi R^{2}}{l}\\\\&=&\dfrac{4\pi 10^{-7}\times\left(10^{3}\right)^{2}\pi\times\left(5\cdot 10^{-2}\right)^{2}}{40\cdot 10^{-2}}\\\\\Rightarrow\,L&=&0.025H \end{array}$
b) Expression de $i(t)$ dans chaque intervalle de temps.
$t\in\left[0\ ;\ 2ms\right]$ ;
$\begin{array}{rcl} i_{0}&=&0\ ;\\\\ a&=&\dfrac{\Delta i}{\Delta t}\\\\&=&\dfrac{0.04-0}{2}\\\\&=&2\cdot 10^{-2}\\\\\Rightarrow\,i(t)&=&2\cdot 10^{-2}t \end{array}$
$t\in\left[2ms\ ;\ 6ms\right]$ ;
$\begin{array}{rcl} i_{0}&=&0.04\cdot 10^{-3}\ ;\\\\ a&=&\dfrac{\Delta i}{\Delta t}\\\\&=&\dfrac{0-0.4}{6-2}\\\\&=& 10^{-2}\\\\\Rightarrow\,i(t)&=&-10^{-2}t+0.04\cdot 10^{-3} \end{array}$
c) Le phénomène qui se produit dans le solénoïde est le phénomène d'induction.
Le solénoïde est le siège d'un courant d'intensité variable, donc une variation du flux qui entraine la création d'un courant induit ou d'une f.é.m induite.
d) Calcul de la f.é.m. induite dans le solénoïde dans des intervalles de temps
$e=-L\dfrac{\mathrm{d}i}{\mathrm{d}t}$
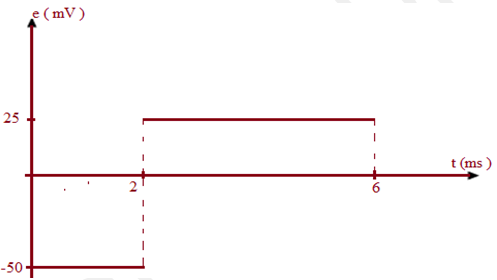
$\begin{array}{rcl} [0\ ;\ 2ms]\ ;\ i{t}&=&2\cdot 10^{-2}t\\\\\Rightarrow\dfrac{\mathrm{d}i}{\mathrm{d}t}&=&2\cdot 10^{-2}\\\\\Rightarrow\,e&=&-0.025\times 2\cdot 10^{-2}\\\\\Rightarrow\,e&=&-50\cdot 10^{-2}V \end{array}$
$\begin{array}{rcl} [2ms\ ;\ 6ms]\ ;\ i{t}&=&-10^{-2}t+0.04\cdot 10^{-3}t\\\\\Rightarrow\dfrac{\mathrm{d}i}{\mathrm{d}t}&=&-10^{-2}\\\\\Rightarrow\,e&=&-0.025\times -10^{-2}\\\\\Rightarrow\,e&=&-25\cdot 10^{-3}V \end{array}$
b) Représentation de f.é.m. au cours du temps. (voir figure)
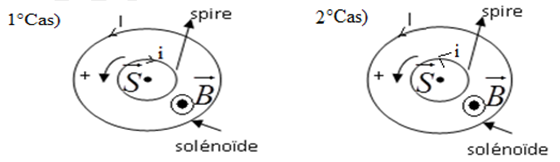
2) a) Représentation du sens du courant induit et du sens du courant principal. sur la spire et sur le solénoïde dans chacun des intervalles
3) a) Calcul de la tension aux bornes du solénoïde.
$u_{S}=ri$

Commentaires
khalifa
sam, 01/27/2024 - 01:11
Permalien
Très important
Ajouter un commentaire