Dénombrement et Probabilités - TL
Classe:
Terminale
I. Dénombrement
Dans cette rubrique, on ne considère que des ensembles finis, c'est-à-dire des ensembles dont on peut compter les éléments.
On appelle cardinal d'un ensemble fini $A$ le nombre de ses éléments.
Il est noté Card$(A).$
Propriétés du cardinal
$\bullet\ \text{Card}\phi=0$
$\bullet\ \text{Si }A\text{ et }B$ sont ensembles finis, $\text{Card}(A\cup B)=\text{Card}(A)+\text{Card}(B)-\text{Card}(A\cap B).$
$\bullet\ A\times B$ Représentant l'ensemble des couples $(a\;,\ b)$ avec $a$ élément de $A$ et $b$ élément de $B$, $\text{Card}(A\times B)=\text{Card}(A)\times\text{Card}(B).$
$P-$listes, arrangements et permutations
Définitions :
1. Soit $E$ un ensemble fini de cardinal $n.$
On appelle $p$-liste de $E$ toute liste ordonnée d'éléments distincts ou non de $E.$
2. Soit $E$ un ensemble fini de cardinal $n$ et $p$ un entier tel que $\leq p\leq n.$
On appelle arrangement à $p$ éléments de $E$ toute $p-$liste d'éléments distincts de $E.$
On appelle permutation de $E$ tout arrangement des $n$ éléments de $E.$
Remarque :
$\bullet\ $Les listes ordonnées de $p$ éléments pris parmi $n$ avec répétition possible sont appelées $p-$listes.
$\bullet\ $Les listes ordonnées de $p$ éléments pris parmi $n$ sans répétition sont appelées arrangements.
Si $p=n$, un arrangement porte le nom de permutation.
Théorèmes :
1. Soit $E$ un ensemble fini de cardinal $n.$
Alors le nombre de $p-$listes de $E$ est $n^{p}.$
2. Soit $E$ un ensemble fini de cardinal $n$ et $p$ un entier tel que $1\leq p\leq n.$
Alors le nombre d'arrangements à $p$ éléments de $E$ est le nombre noté : $A_{n}^{p}=n(n-1)\ldots\ldots(n-p+1)$
$($C'est le produit de $p$ entiers consécutifs décroissant à partir de $n)$, et le nombre de permutations de $E$ est le nombre noté : $n\ !=1\times 2\times\ldots\times n$
$($C'est le produit de tous les entiers de $1$ jusqu'à $n).$
Combinaisons
Définition :
Si $E$ est un ensemble fini, on appelle combinaison à $p$ éléments de $E$ tout sous-ensemble de $E$ de cardinal $p(0\leq p\leq n).$
Remarque :
La combinaison à $0$ élément de $E$ est noté $\Phi.$
Théorème :
Soit $E$ un ensemble fini de cardinal $n.$
Alors le nombre de combinaisons à $p$ éléments de $E$ est le nombre noté :
$C_{n}^{p}=\dfrac{A_{n}^{p}}{p!}=\dfrac{n!}{p!(n-p)!}.$
Propriétés des $C_{n}^{p}$
$\bullet\ C_{n}^{0}=C_{n}^{n}=1$
$\bullet\ C_{n}^{p}=C_{n
}^{n-p}$
}^{n-p}$
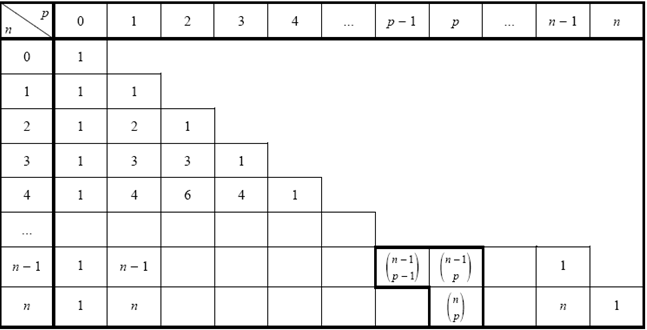
$\bullet\ C_{n}^{p}=C_{n-1}^{p}+C_{n-1}^{p-1}$
(Formule pascal)
Cette dernière formule permet de construire le triangle de Pascal :
Formule du binôme de Newton
Étant donné deux réels $a$ et $b$ un entier naturel, on démontre l'égalité
$(a+b)^{n}=\Sigma_{p=0}^{n}C_{n}^{p}a^{n-p}b^{p}=C_{n}^{0}a^{n}+C_{n}^{1}a^{n-1}b+\ldots+C_{n}^{p}a^{n-p}b^{p}+\ldots+C_{n}^{p}b^{n}.$
2. Probabilités
2.1 Vocabulaire
Une expérience aléatoire est une expérience qu'on peut répéter autant de fois qu'on veut, qui a plusieurs résultats possibles, et dont un seul se produit à la fois, sans qu'on puisse le prévoir.
Exemples :
Lancer d'un dé, d'une pièce de monnaie, tirage d'une carte d'un jeu de $32$ cartes $\ldots.$
L'univers $\Omega$ d'une expérience aléatoire est l'ensemble des résultats possibles.
Exemple :
$\Omega={1\;,\ 2\;,\ 3\;,\ 4\;,\ 5\;,\ 6}$ dans le cas du lancer d'un dé.
Les événements élémentaires sont les résultats possibles d'une expérience aléatoire.
Exemple :
Obtenir $3$ dans le lancer d'un dé.
On appelle événement toute partie de $\Omega$
L'univers $\Omega$ tout entier est l'événement certain.
Un événement impossible est un événement qui ne peut pas se produire $($comme obtenir $7$ dans le lancer d'un dé$).$
Il est noté $\Phi$
Deux événements incompatibles sont deux événements $A$ et $B$ qui ne peuvent pas se produire en même temps : $A\cap B=\Phi.$
On dit alors que $A$ et $B$ sont disjoints.
Deux événements contraires sont deux événements disjoints dont la réunion forme $\Omega$
L'événement contraire de $A$ est noté $\overline{A}.$
2.2 Notion de probabilité
A chaque événement élémentaire $\omega$ d'une expérience aléatoire, on peut associer un nombre $p(\omega)$ élément de l'intervalle $[0\;,\ 1].$
Intuitivement, $p(\omega)$ est la limite de la fréquence de réalisation de l'événement élémentaire quand on répète l'expérience un très grand nombre de fois.
La somme des probabilités de tous les événements élémentaires doit être égale à $1.$
La probabilité d'un événement quelconque $A$ est alors la somme des probabilités des événements élémentaires qui le constituent.
2.3 Propriétés des probabilités
1. Une probabilité est toujours un réel positif en plus petit que $1.$
2. $p(\Omega)=1$ et $p(\Phi)=0.$
3. $p(\overline{A})=1-p(A)\text{ pour tout événement }A$
4. $p(A\cup B)=p(A)+p(B)-p(A\cap B)$, pour tous événements $A$ et $B.$
2.4 Cas de l'équiprobabilité
L'hypothèse d'équiprobabilité dans une expérience aléatoire est celle que tous les événements élémentaires ont la même probabilité.
Alors, pour tout événement $A$, on a :
$$p(A)=\dfrac{\text{Card}A}{\text{Card}\Omega}=\dfrac{\text{Nombre de cas favorables}}{\text{Nombre de cas possibles}}$$

Ajouter un commentaire