Solution des exercices : Travail de la force électrostatique - Énergie potentielle électrostatique - 1er s
Classe:
Première
Exercice 1
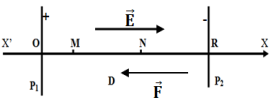
1. Direction et sens (voir figure)
Intensité du champ électrique $\overrightarrow{E}$ qui règne dans le domaine situé $D$ entre les deux plaques
$\begin{array}{rcl} E&=&\dfrac{U}{d}\\&=&\dfrac{500}{10\cdot10^{-2}}\\\Rightarrow\;E&=&50\cdot10^{2}Vm^{-1} \end{array}$
2. Calcul des $d\cdot d\cdot p V_{O}-V_{M}$ ;
$V_{O}-V_{N}$ et $V_{M}-V_{N}$
$\begin{array}{rcl} V_{0}-V_{M}&=&\overrightarrow{E}\cdot\overrightarrow{OM}\\&=&E\times OM\\&=&50\cdot10^{2}\times2\cdot10^{-2}\\\Rightarrow\;V_{0}-V_{M}&=&100V \end{array}$
$\begin{array}{rcl} V_{0}-V_{N}&=&\overrightarrow{E}\cdot\overrightarrow{ON}\\&=&E\times ON\\&=&E\times ON\\&=&50\cdot10^{2}\times7\cdot10^{-2}\\\Rightarrow\;V_{0}-V_{M}&=&3.5\cdot10^{2}V \end{array}$
$\begin{array}{rcl} V_{M}-V_{N}&=&\overrightarrow{E}\cdot\overrightarrow{MN}\\&=&E\times MN\\&=&50\cdot10^{2}\times\left|7\cdot10^{-2}-2\cdot10^{-2}\right|\\\Rightarrow\;V_{M}-V_{N}&=&2.5\cdot10^{2}V \end{array}$
3.1 Caractéristiques de la force électrostatique $\overrightarrow{F}$ qui s'exerce sur l'électron
Direction et sens (voir figure)
Intensité :
$\begin{array}{rcl} F&=&qE\\&=&1.6\cdot 1.6\cdot10^{-19}\times50\cdot10^{2}\\\Rightarrow\;F&=&80\cdot10^{-17}N \end{array}$
3.2 Vitesse de l'électron à son passage en $N$, $M$, puis en $O$
Appliquons le théorème de l'énergie cinétique :
Entre $R$ et $N$ :
$\begin{array}{rcl} E_{C_{N}}-E_{C_{R}}&=&W_{NR}\left(\overrightarrow{F}\right)+W_{NR}\left(\overrightarrow{P}\right)\\\Rightarrow\dfrac{1}{2}m_{e}V_{N}^{2}-0&=&-eU_{RN}+0\\\Rightarrow\dfrac{1}{2}m_{e}V_{N}^{2}-0&=&-e\times-\left(U-U_{ON}\right) \end{array}$
$\begin{array}{rcl} V_{N}&=&\sqrt{\dfrac{2e\left(U-U_{ON}\right)}{me}}\\&=&\sqrt{\dfrac{2\times1.6\cdot10^{-19}\times\left(500-3.5\cdot10^{2}\right)}{9.1\cdot10^{-31}}}\\\Rightarrow\;V_{N}&=&7.3\cdot10^{6}m\cdot s^{-1} \end{array}$
$\begin{array}{rcl} V_{M}&=&\sqrt{\dfrac{2e\left(U-U_{OM}\right)}{m_{e}}}\\&=&\sqrt{\dfrac{2\times1.6\cdot10^{-19}\times(500-100)}{9.1\cdot10^{-31}}}\\\Rightarrow\;V_{N}&=&11\cdot10^{6}m\cdot s^{-1} \end{array}$
$\begin{array}{rcl} V_{O}&=&\sqrt{\dfrac{2e\left(U-U_{OO}\right)}{m_{e}}}\\&=&\sqrt{\dfrac{2\times1.6\cdot10^{-19}\times(500-0)}{9.1\cdot10^{-31}}}\\\Rightarrow\;V_{o}&=&13\cdot10^{6}m\cdot s^{-1} \end{array}$
4. Calculer le travail $W\left(\overrightarrow{F}\right)$ de la force lorsque l'électron déplace de $N$ à $M$
$\begin{array}{rcl} W\left(\overrightarrow{F}\right)&=&-e\left(V_{N}-V_{M}\right)\\&=&-e\times-\left(V_{M}-V_{N}\right)\\&=&e\times\left(V_{M}-V_{N}\right)\\&=&1.6\cdot10^{-19}\times2.5\cdot10^{2}\\\Rightarrow\;W \left(\overrightarrow{F}\right)&=&4.0\cdot10^{-17}J \end{array}$
Exercice 2
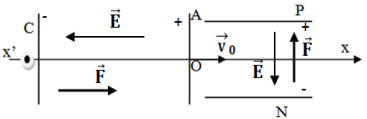
1.1 Détermination des caractéristiques du vecteur champ électrostatique entre $C$ et $A$
Direction et sens (voir figure)
Intensité du champ électronique $\overrightarrow{E}$
$\begin{array}{rcl} E&=&\dfrac{U_{AC}}{CA}\\&=&\dfrac{640}{5\cdot10^{-2}}\\\Rightarrow\;E&=&12.8\cdot10^{3}V\cdot m^{-1} \end{array}$
1.2 Calcul du travail de la force électrostatique appliquée à un électron pour aller de $C$ à $A$
$\begin{array}{rcl} W_{CA}\left(\overrightarrow{F}\right)&=&-eU_{CA}\\&=&-e\times-U_{AC}\\&=&eU_{AC}\\&=&1.6\cdot10^{-19}\times640\\\Rightarrow\;w_{CA}\left(\overrightarrow{F}\right)&=&1.0\cdot10^{-16}J \end{array}$
2. Calcul de la tension $U_{OM}$
$\begin{array}{rcl} U_{OM}&=&\overrightarrow{E}\cdot\overrightarrow{OM}\\&=&-E\times OM\text{ or }E\\&=&\dfrac{U_{PN}}{d}\\\Rightarrow\;U_{OM}&=&-\dfrac{U_{PN}}{d}\times d'\\&=&-\dfrac{1000}{5}\times 2\\\Rightarrow\;U_{OM}&=&-400V \end{array}$
3. Calcul de l'énergie potentielle électrostatique d'un électron en $O$ et en $M.$
$E_{p}=qV+\text{cte}$ ;
$\begin{array}{rcl} Q_{1}+Q_{2}&=&0\\\Rightarrow\left(\rho_{\text{eau}}V_{0}C_{\text{eau}}+\mu\right)\left(\theta_{4}-\theta_{0}\right)-m'L_{v}+m'C_{\text{eau}}\left(\theta_{4}-\theta_{3}\right)&=&0\\\Rightarrow\;-m'L_{v} &=&\left(\rho_{\text{eau}}V_{0}C_{\text{eau}}+\mu\right)\left(\theta_{0}-\theta_{4}\right)+m'C_{\text{eau}}\left(\theta_{3}-\theta_{4}\right)\\\Rightarrow\;L_{v}&=&-\dfrac{\left(\rho_{\text{eau}}V_{0}C_{\text{eau}}+\mu\right)\left(\theta_{0}-\theta_{4}\right)+m'C_{\text{eau}}\left(\theta_{3}-\theta_{4}\right)}{m'}\\\Rightarrow\;L_{v}&=&-\dfrac{\left(1\times450\cdot10^{-3}\times4185+100\right)(20.0-45.2)+20.0\cdot10^{-3}\times4185(100-45.2)}{20.0\cdot10^{-3}}\\\Rightarrow\;L_{v}&=&2.27\cdot10^{6}J\cdot kg^{-1} \end{array}$
4. Détermination du travail de la force électrostatique s'exerçant sur un électron pour aller de $O$ à
$\begin{array}{rcl} W_{OM}\left(\overrightarrow{F}\right)&=&-\Delta E_{p}\\&=&-\left(E_{P_{M}}-E_{P_{o}}\right)\\&=& \left(-14.4\cdot10^{-17}-8.0\cdot10^{-17}\right)\\\Rightarrow\;W_{OM}\left(\overrightarrow{F}\right)&=&6.4\cdot10^{-17} \end{array}$
5. Calcul de :
5.1. L'énergie cinétique de sortie $E_{CM}$ de l'électron en $M.$
Appliquons le théorème de l'énergie cinétique
$\begin{array}{rcl} W_{OM}\left(\overrightarrow{F}\right)&=&\Delta E_{C}\\&=&E_{C_{M}}-E_{C_{o}}\\&=&W_{OM}\left(\overrightarrow{F}\right)\\\Rightarrow\;E_{C_{M}}&=&W_{OM}\left(\overrightarrow{F}\right)+E_{C_{o}}\\\text{or }E_{C_{o}}=E_{C_{A}}=-eU_{CA}=-e\times -U_{AC}\\\Rightarrow\;E_{C_{M}}&=&W_{OM}\left(\overrightarrow{F}\right)+eU_{AC}\\\Rightarrow\;E_{C_{M}}&=&6.4\cdot10^{-17}+1.6\cdot 10^{-19}\times 640\\\Rightarrow\;E_{C_{M}}&=&7.4\cdot10^{-17}J \end{array}$
5.2 La vitesse de l'élection $V_{M}$ au point $M.$
$\begin{array}{rcl} E_{C_{M}}&=&\dfrac{1}{2}mV_{M}^{2}\\\Rightarrow\;V_{M}^{2}&=&\dfrac{2E_{C_{M}}}{m}\\\Rightarrow\;V_{M}&=&\sqrt{\dfrac{2E_{C_{M}}}{M}}\\&=&\sqrt{\dfrac{2\times7.4\cdot10^{-17}}{9.1\cdot10^{-31}}}\\\Rightarrow\;V_{M}&=&13\cdot10^{6}m\cdot s^{-1} \end{array}$
Exercice 3
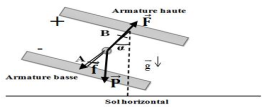
1. Inventaire des forces que subit la particule au cours de son déplacement de $A$ vers $B.$
La particule est soumise à : son poids $\overrightarrow{P}$ , la force électrostatique $\overrightarrow{F}$ et aux forces de frottement $\overrightarrow{F}$
2. Le poids $\overrightarrow{P}$ et la force électrostatique $\overrightarrow{F}$ sont des forces conservatives (le travail d'une force conservative ne dépend pas du chemin suivi)
3. Expression du travail de la force de frottement de l'air $f$ en fonction de $AB$ et $f.$
$W_{AB}\left(\overrightarrow{f}\right)=-f\times AB$
4. Le signe de la charge électrique de l'armature haute est positif car les électrons chargés négativement se déplacent vers l'armature chargée positivement
5. Représentation du champ électrique $E$ et du champ de pesanteur $g$ sur la figure.
(Voir figure
6. Expression du travail de la force électrique $Fe$ et du poids $P$, en fonction de $m$, $q$ $V_{A}$, $V_{B}$, $g$, $\alpha$ et $AB.$
$W_{AB}\left(\overrightarrow{F_{e}}\right)=q\left(V_{A}-V_{B}\right)$
$W_{AB}\left(\overrightarrow{P}\right)=-mgAB\cos\alpha$
7. Précisons pour chacune de ces forces si leur travail est moteur ou résistant.
$-\ $Le travail de la force électronique $\overrightarrow{F_{e}}$ est moteur car il favorise le déplacement.
$-\ $Le travail de la force électrostatique $\overrightarrow{P}$ est résistance car il s'oppose au déplacement.
8. Calcul du travail de ces forces sur le trajet $AB=1.8\,m$
$\begin{array}{rcl} W_{AB}\left(\overrightarrow{F_{e}}\right)&=&q\left(V_{A}-V_{B}\right)\\&=&-2e\left(V_{A}-V_{B}\right)\\&=&-2\times1.6\cdot10^{-19}(-3-5)\\\Rightarrow\;W_{AB}\left(\overrightarrow{F_{e}}\right)&=&16\cdot10^{-19}J \end{array}$
$\begin{array}{rcl} W_{AB}\left(\overrightarrow{P}\right)&=&-mgAB\cos\alpha\\&=&-3.210^{-27}\times 10\times 1.8\cos 30^{\circ}\\\Rightarrow\;W_{AB}\left(\overrightarrow{P}\right)&=&5.0\cdot10^{26}J \end{array}$
$W_{AB}\left(\overrightarrow{F_{e}}\right)\succ W_{AB}\left(\overrightarrow{P}\right)$, on peut négliger l'énergie potentielle de pesanteur de la particule.
Alors, on ne prend en compte que l'énergie potentielle électrique.
9. Déduction de l'expression de l'énergie mécanique de la particule au point $A$ en fonction de sa vitesse $v_{A}$
et des grandeurs $V_{A}$, $q$ et $m$
$\begin{array}{rcl} E_{m_{A}}&=&E_{P_{A}}+E_{C_{A}}\\\Rightarrow\;E_{m_{A}}&=&qV_{A}+\dfrac{1}{2}mv_{A}^{2} \end{array}$
10 Déduction de l'expression de l'énergie mécanique de la particule au point $B$ en fonction de la vitesse $v_{B}$
et des grandeurs $V_{B}$, $q$, et $m.$
$\begin{array}{rcl} E_{m_{B}}&=&E_{P_{B}}+E_{C_{B}}\\\Rightarrow\;E_{m_{B}}&=&qV_{B}+\dfrac{1}{2}mv_{B}^{2} \end{array}$
11 L'énergie mécanique se conserve car il y a un vide parfait ; les forces de frottement sont négligeables
12. Déduction de la vitesse $v_{B}$ de la particule
La conservation de l'énergie mécanique s'écrit :
$\begin{array}{rcl} E_{m_{B}}&=&E_{m_{A}}\\\Rightarrow\;qV_{B}+\dfrac{1}{2}mv_{B}^{2}&=&qV_{A}+\dfrac{1}{2}mv_{A}^{2}\\\Rightarrow\dfrac{1}{2}mv_{B}^{2}&=&q\left(V_{A}-V_{B}\right)+\dfrac{1}{2}mv_{A}^{2}\\\Rightarrow\;V_{B}&=&\sqrt{\dfrac{2q\left(V_{A}-V_{B}\right)}{m}+v_{A}^{2}}\\\Rightarrow\;V_{B} &=&\sqrt{\dfrac{-2\times1.6\cdot10^{-19}(-3-5)}{3.2\cdot10^{-27}}+(0.53)^{2}}\\\Rightarrow\;V_{B}&=&28\cdot10^{3}m\cdot s^{-1} \end{array}$
Exercice 4
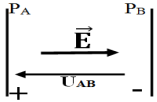
1. Expression du travail de la force électrostatique $\overrightarrow{F}$
$\begin{array}{rcl} W_{AB}\left(\overrightarrow{F}\right)&=&q\overrightarrow{E}\cdot\overrightarrow{AB}\\&=&qE\times AB \end{array}$
2. Montrons que le travail de cette force s'écrit :
$\begin{array}{rcl}W_{AB}\left(\overrightarrow{F}\right)&=&qU_{AB} W_{AB}\left(\overrightarrow{F}\right)\\&=&q\overrightarrow{E}\cdot\overrightarrow{AB}\text{ or }\overrightarrow{E}\cdot\overrightarrow{AB}=U_{AB}\\\Rightarrow\;W_{AB}\left(\overrightarrow{F}\right)&=&qU_{AB} \end{array}$
3. Calcul de sa valeur dans le cas d'un noyau d'hélium $He^{2+}$ se déplaçant de $A$ à $B$
$\begin{array}{rcl} W_{AB}\left(\overrightarrow{F}\right)&=&qU_{AB}\\&=&2e\times U_{AB}\\&=&2\times 1.60\cdot10^{-19}\times400\\\Rightarrow\;W_{AB}\left(\overrightarrow{F}\right)&=&12.8\cdot10^{-19}J \end{array}$
Exercice 5
1. Charge $q_{\alpha}$ de la particule $\alpha$
$\begin{array}{rcl} q_{\alpha}&=&2e\\&=&2\times1.60\cdot10^{-19}\\\Rightarrow\;q_{\alpha}&=&3.20\cdot10^{-19}C \end{array}$
2. Établissement de l'expression du travail de la force électrostatique et expression du travail en fonction $q_{\alpha}$, $V_{A}$ et $V_{B}$
$\begin{array}{rcl} W_{AB}\left(\overrightarrow{F}\right)&=&q\alpha\overrightarrow{E}\cdot\overrightarrow{AB}\\\text{or }\overrightarrow{E}\cdot\overrightarrow{AB}&=&V_{A}-V_{B}\\\Rightarrow\;W_{AB}\left(\overrightarrow{F}\right)&=&q\alpha\left(V_{A}-V_{B}\right) \end{array}$
3. Déduction de l'expression de la variation d'énergie potentielle électrique entre $A$ et $B$
$\begin{array}{rcl} W_{AB}\left(\overrightarrow{F}\right)&=&q_{\alpha}\overrightarrow{E}\cdot\overrightarrow{AB}\\\text{ or }\overrightarrow{E}\cdot\overrightarrow{AB}&=&q_{\alpha}\left(V_{A}-V_{B}\right)\\\Rightarrow\Delta E_{p}&=&-q_{\alpha}\left(V_{A}-V_{B}\right) \end{array}$
4. L'énergie mécanique se conserve car les frottements sont négligeables lors de ce mouvement
5.1. Expression de la différence de potentiel $V_{A}-V_{B}$ en fonction de $v_{B}$, $m_{\alpha}$ et $q_{\alpha}$
La conservation de l'énergie mécanique s'écrit :
$\begin{array}{rcl} -\Delta E_{p}&=&\Delta E_{c}\\\Rightarrow\;q\alpha\left(V_{A}-V_{B}\right)&=&\dfrac{1}{2}m_{\alpha }v_{B}^{2}-0\\\Rightarrow\;V_{A}-V_{B}&=&\dfrac{m_{\alpha} v_{B}^{2}}{2q_{\alpha}} \end{array}$
5.2 Calcul de la valeur de la différence de potentiel $V_{A}-V_{B}$
$\begin{array}{rcl} V_{A}-V_{B}&=&\dfrac{m_{\alpha}v_{B}^{2}}{2q_{\alpha}}\\&=&\dfrac{6.70\cdot10^{-27}\times\left(1.00\cdot10^{6}\right)^{2}}{2\times2\times1.60\cdot10^{-19}}\\\Rightarrow\;V_{A}-V_{B}&=&1.05\cdot10^{4}V \end{array}$
Exercice 6
1. Détermination des constantes $a$ et $b.$
$E=a+bz$
$\begin{array}{rcl} z=0\;,E&=&100V\cdot m^{-1}\\\Rightarrow\;E&=&a+b\times 0\\&=&100V\cdot m^{-1}\\\Rightarrow\alpha&=&100V\cdot m^{-1} \end{array}$
$\begin{array}{rcl} z=140m\;,E&=&20V\cdot m^{-1}\\\Rightarrow\;E&=&100+1400b\\&=&20V\cdot m^{-1}\\\Rightarrow\;b&=&\dfrac{20-100}{1400}\\\Rightarrow\;b&=&-5.7\cdot10^{-2}V\cdot m^{-2}\\\Rightarrow\;E&=&100-5.7\cdot10^{-2}z \end{array}$
Les constantes $a$ et $b$ sont respectivement $V\cdot m^{-1}$ et $V\cdot m^{-2}$
Représentation graphique $E$ en fonction de $z$
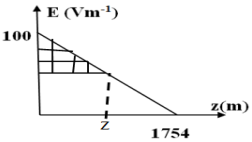
2. Détermination du travail des forces électriques s'exerçant sur la charge par une méthode graphique.
$\begin{array}{rcl} W\left(\overrightarrow{F}\right)&=&\dfrac{1}{2}qEz\\\text{or }E&=&a+bz\\\Rightarrow\;W\left(\overrightarrow{F}\right)&=&\dfrac{1}{2}q(a+bz)z\\\Rightarrow\;W\left(\overrightarrow{F}\right)&=&\dfrac{1}{2}\times10^{-10}\left(100-5.7\cdot10^{-2}z\right)z \end{array}$
Déduction du potentiel électrostatique d'un point situé à l'altitude $h$
$\begin{array}{rcl} W\left(\overrightarrow{F}\right)&=&qU\\&=&\dfrac{1}{2}q(a+bz)z\\\Rightarrow\;U&=&\dfrac{1}{2}(a+bz)\ ;\ z\\&=&h\\\Rightarrow\;U&=&\dfrac{1}{2}(a+bh)h\\\Rightarrow\;U&=&\dfrac{1}{2}(a+bh)h\\\Rightarrow\;U&=&\dfrac{1}{2}\left(100-5.7\cdot10^{-2}h\right)h \end{array}$
3. Calcul de l'énergie potentielle de pesanteur et de l'énergie potentielle électrostatique de cet ion.
$\begin{array}{rcl} E_{pp}&=&mgz\\&=&\dfrac{1.0\cdot10^{-3}}{6.02\cdot10^{23}}\times10\times1400\\\Rightarrow\;E_{pp}&=&2.3\cdot10^{-23}J \end{array}$
$\begin{array}{rcl} E_{PE}&=&\dfrac{1}{2}q(a+bz)z\\&=&\dfrac{1}{2}\times1.6\cdot10^{-19}\left(100-5.7\cdot10^{-2}\times1400\right)\times1400\\ \Rightarrow\;E_{PE}&=&16.2\cdot10^{-19}J \end{array}$
L'énergie potentielle électrostatique est grande devant l'énergie potentielle de pesanteur.
Cette dernière peut être négligée
Vitesse de l'ion à l'arrivée sur le sol
Appliquons la conservation de l'énergie mécanique
$\begin{array}{rcl} E_{C_{f}}+E_{P_{f}}&=&E_{C_{I}}+E_{P_{I}}\\\Rightarrow\;E_{C_{f}}+0&=&0+E_{P_{I}}\\\Rightarrow\dfrac{1}{2}mv^{2}&=&E_{P_{I}}\\\Rightarrow\;v&=&\sqrt{\dfrac{2E_{P_{I}}}{m}}\\&=&\sqrt{\dfrac{2\times16.2\cdot10^{-19}\times6.02\cdot10^{23}}{1.0\cdot10^{-3}}}\\\Rightarrow\;v&=&44\cdot10^{3}m\cdot s^{-1} \end{array}$
Exercice 7
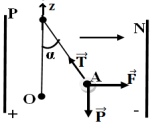
1. Calcul de la charge $q$ du pendule si, à l'équilibre
La condition d'équilibre, appliquée à la sphère, s'écrit :
$\begin{array}{rcl} \overrightarrow{P}+\overrightarrow{F} \overrightarrow{T}&=&\overrightarrow{0}\\&\Rightarrow&\left\lbrace\begin{array}{lcl} 0+F-T\sin\alpha&=&0\\ mg+0-T\cos\alpha&=&0 \end{array}\right.\\&\Rightarrow&\left\lbrace\begin{array}{lcl} T\sin\alpha&=&F\quad(1)\\ T\cos\alpha&=&mg\quad(2) \end{array}\right.\\\Rightarrow\tan\alpha&=&\dfrac{qE}{mg}\\\Rightarrow\;q&=&\dfrac{m\times g\times\tan\alpha}{E}\\\text{ or }E&=&\dfrac{U_{PN}}{d}\\\Rightarrow\;q&=&\dfrac{mgd\tan\alpha}{U_{PN}}\\&=&\dfrac{0.5\cdot10^{-3}\times10\times15\cdot10^{-2}\times\tan 30^{\circ}}{1500V}\\ \Rightarrow\;q&=&2.9\cdot10^{-7}C \end{array}$
2. Expression en fonction de $\alpha$ l'énergie potentielle de pesanteur $\varepsilon pg$ et l'énergie potentielle électrostatique
$\varepsilon pe.$
$\varepsilon pg=mgz+\text{cte}$
$\begin{array}{rcl} \varepsilon pg(z=0)&=&mg\times 0+\text{cte}\\&=&0\\\Rightarrow\text{cte}&=&0\\\Rightarrow\varepsilon&=&mgz \end{array}$
$\begin{array}{rcl} Z_{A}&=&1-1\cos\alpha\\&=&1(1-\cos\alpha)\\\Rightarrow\varepsilon_{pg}&=&mgl(1-\cos\alpha) \end{array}$
$\begin{array}{rcl} \Delta\varepsilon pe&=&-W\left(\overrightarrow{F}\right)\\\Rightarrow\varepsilon pe-0&=&-Fl\sin\alpha\\\text{ or }F&=&qE\\&=&q\dfrac{U_{PN}}{d}\\\Rightarrow\varepsilon pe&=&-q\dfrac{U_{PN}}{d}l\sin\alpha \end{array}$
Valeur de $\alpha$ pour laquelle la somme $\varepsilon P$ de ces énergies potentielles est minimale
$\begin{array}{rcl} \varepsilon_{p}&=&\varepsilon_{pg}+\varepsilon_{pe}\\&=&mgl(l-\cos\alpha)-q\dfrac{U_{PN}}{d}l\sin\alpha\\\Rightarrow\varepsilon'_{p}&=&mgl\sin\alpha-q\dfrac{U_{PN}}{d}l\cos\alpha\\&=&0\\\Rightarrow\;mgl\sin\alpha&=&q\dfrac{U_{PN}}{d}l\cos\alpha\\\Rightarrow\dfrac{\sin\alpha}{\cos\alpha}&=&\dfrac{qU_{PN}}{mgd}\\ \Rightarrow\tan\alpha&=&\dfrac{qU_{PN}}{mgd}\\\Rightarrow\alpha&=&\tan^{-1}\left(\dfrac{qU_{PN}}{mgd}\right)\\ \Rightarrow\alpha&=&\tan^{-1}\left(\dfrac{2.9\cdot 10^{-7}\times 1500}{0.5\cdot10^{-3}\times 10\times 15\cdot10^{-2}}\right)\\\Rightarrow\alpha&=&30^{\circ} \end{array}$
Conclure.
Données : masse de la sphère : $m=0.5\;g$ ; longueur du fil : $1=20\;m$ ; $g=10\;m\cdot s^{2}$
Exercice 8
1. Calcul du travail de la force électrostatique qui s'exerce sur cet élection
$\begin{array}{rcl} W\left(\overrightarrow{F}\right)&=&-eU\\&=&-1.60\cdot10^{-19}\times200\\ \Rightarrow\;W\left(\overrightarrow{F}\right)&=&-3.20\cdot10^{-17}J \end{array}$
$\begin{array}{rcl} W\left(\overrightarrow{F}\right)&=&\dfrac{-3.20\cdot10^{-17}}{1.60\cdot10^{-19}}\\\Rightarrow\;W\left(\overrightarrow{F}\right)&=&-200eV \end{array}$
2/ Caractérisation du champ électrostatique en tout point de l'espace compris entre les plaques.
Le champ électrostatique en tout point de l'espace a même direction, même sens et même intensité
$\begin{array}{rcl} E&=&\dfrac{U}{d}\\&=&\dfrac{200}{2\cdot10^{-2}}\\\Rightarrow\;E&=&10\cdot10^{3}V \end{array}$
3. Calcul du travail de la force et caractérisation du champ électrostatique
$\begin{array}{rcl} W\left(\overrightarrow{F}\right)&=&-eU\\&=&-1.60\cdot10^{-19}\times\\\Rightarrow\;W\left(\overrightarrow{F}\right)&=&-3.20\cdot 10^{-17}J \end{array}$
$\begin{array}{rcl} W\left(\overrightarrow{F}\right)&=&\dfrac{-3.20\cdot10^{-17}}{1.60\cdot10^{-19}}\\\Rightarrow\;W\left(\overrightarrow{F}\right)&=&-200eV \end{array}$
Le champ électrostatique en tout point de l'espace a même direction, même sens et même intensité
$\begin{array}{rcl} E'&=&\dfrac{U}{d'}\\&=&\dfrac{200}{4\cdot10^{-2}}\\\Rightarrow\;E'&=&5\cdot10^{3}V \end{array}$
Le travail de la force électrostatique ne dépend que de la charge et de la différence de potentiel (d.d.p)
4. On peut toujours calculer simplement le travail de la force électrostatique qui s'exerce sur l'électron allant
de la plaque positive à la plaque négative.
Il suffit de connaitre la différence de potentiel ou la tension entre deux les plaques
Exercice 9
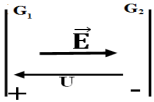
1. Vitesse $V_{1}$ minimale des électrons qui parviennent à traverser la grille $G_{2}$
La conservation de l'énergie mécanique entre les grilles $G_{1}$ et $G_{2}$ s'écrit :
$\begin{array}{rcl} E_{m_{1}}&=&E_{m_{2}}\\\Rightarrow\;-eV_{1}+\dfrac{1}{2}mv_{1}^{2}&=&-eV_{2}+0\\\Rightarrow\dfrac{1}{2}mv_{1}^{2}&=&-e\left(V_{2}-V_{1}\right)+\dfrac{1} {2}mv_{1}^{2}\\\Rightarrow\;v_{1}&=&\sqrt{\dfrac{-2e\left(V_{2}-V_{1}\right)}{m}}\\\Rightarrow\;v_{1} &=&\sqrt{\dfrac{-2\times1.6\cdot10^{-19}\times-100}{9.1\cdot10^{-31}}}\\\Rightarrow\;v_{1}&=&5.9\cdot10^{6}m\cdot s^{-1} \end{array}$
2. Vitesse $V_{2}$ d'un électron traversant $G_{2}$
La conservation de l'énergie mécanique entre les grilles $G_{1}$ et $G_{2}$ s'écrit :
$\begin{array}{rcl} E_{m_{2}}&=&E_{m_{1}}\\\Rightarrow\;-eV_{2}+\dfrac{1}{2}mv_{2}^{2}&=&-eV_{1}+\dfrac{1}{2}mv_{1}^{2}\\\Rightarrow\dfrac{1}{2}mv_{2}^{2}&=&-e\left(V_{A}-V_{B}\right)+\dfrac{1}{2}mv_{1}^{2}\\\Rightarrow\;v_{2}&=&\sqrt{\dfrac{-2e\left(V_{1}-V_{2}\right)}{m}+v_{1}^{2}}\\\Rightarrow\;v_{2}&=&\sqrt{\dfrac{-2\times1.6\cdot^{-19}\times 100}{9.1\cdot10^{-31}}+\left(9\cdot10^{6}\right)^{2}}\\\Rightarrow\;v_{2}&=&1.8\cdot10^{6}m\cdot s^{-1} \end{array}$
3.Vitesse avec laquelle l'élection retraverse $G_{1}$
Au cours d'un choc élastique il y a conservation de l'énergie cinétique et conservation de la quantité de mouvement du système (électrons, neutron).
$\begin{array}{rcl} \overrightarrow{m_{e}v_{e}}+\overrightarrow{0}&=&\overrightarrow{m_{e}v_{e}^{'}}+\overrightarrow{m_{n}v_{n}}\\\Rightarrow\;m_{e}v_{e}&=&-m_{e}v^{'}+m_{n}v_{n}\\\Rightarrow\;m_{e}\left(v_{e}+v_{e}^{'}\right)&=&m_{n}v_{n}\\\Rightarrow\;m_{e}\left(v_{e}+v_{e}^{'}\right)&=&1840\,m_{e}v_{n}\\\Rightarrow\;v_{e}+v_{e}^{'}&=&1840\,v_{n}\quad(1) \end{array}$
$\begin{array}{rcl} \dfrac{1}{2}m_{e}v_{e}^{2}+0&=&\dfrac{1}{2}m_{e}v_{2}^{'2}+\dfrac{1}{2}m_{n}v_{n}^{2}\\\Rightarrow\;m_{e}\left(v_{e}^{2}-v_{e}^{'2}\right)&=&m_{n}v_{n}^{2}\\\Rightarrow\;m_{e}\left(v_{e}^{2}-v_{e}^{'2}\right)&=&1840m_{e}v_{n}^{2}\quad(2)\\\Rightarrow\;v_{e}^{2}-v_{e}^{'2}&=&1840\,v_{n}^{2}\quad(2) \end{array}$
$\begin{array}{rcl} &\Rightarrow&\dfrac{(2)}{(1)}\\&\Rightarrow&\;v_{e}-v_{e}^{'}=1840\,v_{n}\\&\Rightarrow&\left\lbrace\begin{array}{lcl} v_{e}+v_{e}^{'}&=&1840\,v_{n}\\ v_{e}-v_{e}^{'}&=&1840\,v_{n} \end{array}\right.\\\Rightarrow\;v_{e}+v_{e}^{'}&=&v_{e}-v_{e}^{'}\\\Rightarrow\;2v_{e}^{'}&=&v_{e}-v_{e}\\\Rightarrow\;v_{e}^{'}&=&0m\cdot s^{-1} \end{array}$
Exercice 10
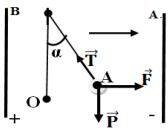
2.2. Calcul de l'intensité du champ électrique
La condition d'équilibre, appliquée à la boule, s'écrit :
$\begin{array}{rcl} \overrightarrow{P}+\overrightarrow{F}+\overrightarrow{T}&=&0\\&\Rightarrow&\left\lbrace\begin{array}{lcl} 0+F-T\sin\alpha&=&0\\ mg+0-T\cos\alpha&=&0 \end{array}\right.\\&\Rightarrow&\left\lbrace\begin{array}{lcl} T\sin\alpha&=&F\quad(1)\\T\cos\alpha&=& mg\quad(2) \end{array}\right.\\\text{ or }F&=&|q|E\\\Rightarrow\tan\alpha&=&\dfrac{|q|E}{mg}\\\Rightarrow\;E&=&\dfrac{mg\tan\alpha}{|q|}\\\Rightarrow\;E&=&\dfrac{2.5\cdot10^{-3}\times10\times\tan30^{\circ}}{|-0.50|\cdot10^{-6}}\\\Rightarrow\;E&=&2.9\cdot10^{4}Vm^{-1} \end{array}$
2.3 Angle d'inclinaison du fil par rapport à la verticale
$\begin{array}{rcl} \overrightarrow{P}+\overrightarrow{F}+\overrightarrow{T}&=&0\\&\Rightarrow&\left\lbrace\begin{array}{lcl} 0+F-T\sin\alpha&=&0\\ mg+0-T\cos\alpha&=&0 \end{array}\right.\\&\Rightarrow&\left\lbrace\begin{array}{lcl} T\sin\alpha&=&F\quad(1)\\ T\cos\alpha&=&mg\quad(2) \end{array}\right.\\\Rightarrow\tan\alpha&=&\dfrac{|q|E}{mg}\\\Rightarrow\alpha&=&\tan^{-1}(\dfrac{|q|E}{mg})\\&=&\tan^{-1}\left(\dfrac{|0.50|\cdot10^{-6}\times1.0\cdot10^{4}}{2.5\cdot10^{-3}\times10}\right)\\\Rightarrow\alpha&=&11^{\circ} \end{array}$

Commentaires
Anonyme (non vérifié)
mer, 03/20/2024 - 15:32
Permalien
Perfect
Anonyme (non vérifié)
mer, 03/20/2024 - 15:35
Permalien
perfect
Marcel (non vérifié)
jeu, 03/28/2024 - 07:49
Permalien
Demande de téléchargement
Ajouter un commentaire