Solution des exercices : Condensateurs : capacité, énergie emmagasinée - 1er s
Classe:
Première
Exercice 1
1. Tracé du graphique $U=f(t)$
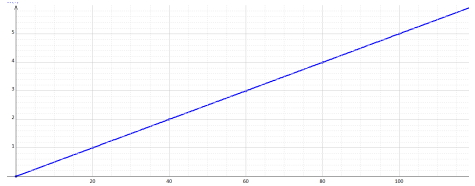
Le graphe $U=f(t)$ est une fonction linéaire du temps
2. Détermination de la variation de $U$ en fonction du temps.
$\begin{array}{rcl} U&=&kt\\\text{ avec }k&=&\dfrac{\Delta U}{\Delta t}\\&=&\dfrac{4.5-3.5}{(90-70)\cdot10^{-3}}\\\Rightarrow\;K&=&50\,V_{s}^{-1}\\\Rightarrow\;U&=&50\,t \end{array}$
Déduction de la capacité du condensateur
$\begin{array}{rcl} q&=&It\\&=&Cu\\\text{ or }u&=&50t\\\Rightarrow\;q&=&It\\&=&50Ct\\\Rightarrow\;C&=&\dfrac{I}{50}\\&=&\dfrac{0.5\cdot10^{-3}}{50}\\\Rightarrow\;C&=&1.0\cdot10^{-5}F \end{array}$
Exercice 2
1. Calcul la capacité équivalente pour chaque schéma
$\begin{array}{rcl} \text{a. }\quad\dfrac{1}{C_{\text{éq}}}&=&\dfrac{1}{C_{1}}+\dfrac{1}{C_{2}}+\dfrac{1}{C_{3}}\\\Rightarrow\dfrac{1}{C_{\text{éq}}}&=&\dfrac{C_{2}C_{3}}{C_{1}C_{2}C_{3}}+\dfrac{C_{1}C_{2}}{C_{1}C_{2}C_{3}}+\dfrac{C_{1}C_{2}}{C_{1}C_{2}C_{3}}\\\Rightarrow\;C_{\text{éq}}&=&\dfrac{C_{1}C_{2}C_{3}}{C_{1}C_{2}+C_{1}C_{3}+C_{2}C_{3}}\\\Rightarrow\;C_{\text{éq}}&=&\dfrac{10\cdot10^{-6}\times2\cdot10^{-6}\times1000\cdot10^{-9}}{10\cdot10^{-6}\times2\cdot10^{-6}+10\cdot10^{-6}\times1000\cdot10^{-9}+2\cdot10^{-6}\times1000\cdot10^{-9}}\\\Rightarrow\;C_{\text{éq}}&=&0.625\cdot10^{-6}F \end{array}$
$\begin{array}{rcl}\text{b. } \quad C_{\text{éq}}&=&C_{1}+C_{2}+C_{3}\\&=&10\cdot10^{-6}+2\cdot10^{-6}+1000\cdot10^{-9}\\\Rightarrow\;C_{\text{éq}}&=&2.7\cdot10^{-6}F \end{array}$
$\begin{array}{rcl}\text{c. }\quad C_{\text{éq}}&=&\dfrac{C_{2}C_{1}}{C_{2}+C_{1}}+C_{3}\\&=&\dfrac{2\cdot10^{-6}\times10\cdot10^{-6}} {2\cdot10^{-6}+10\cdot10^{-6}}+1000\cdot10^{-9}\\\Rightarrow\;C_{\text{éq}}&=&2.7\cdot10^{-6}F \end{array}$
2. Déterminer la valeur de $C_{AB}$
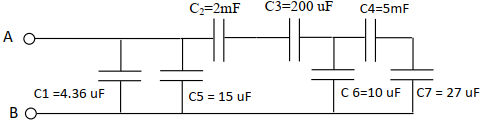
$\begin{array}{rcl} \dfrac{1}{C_{\text{éq}}}&=&\dfrac{1}{C_{1}+C_{3}}+\dfrac{1}{C_{2}}+\dfrac{1}{C_{3}}+\dfrac{1}{C_{6}+\dfrac{C_{4}C_{7}}{C_{4}+C_{7}}}\\\Rightarrow\;C_{\text{éq}}&=&\dfrac{1}{\dfrac{1}{C_{1}+C_{5}+\dfrac{1}{C_{2}+\dfrac{1}{C_{3}+\dfrac{1}{C_{6}+\dfrac{C_{4}C_{7}}{C_{4}+C_{7}}}}}}}\\\Rightarrow\;C_{\text{éq}}&=&\dfrac{1}{\dfrac{1}{4.36+5000}+\dfrac{1}{2000}+\dfrac{1}{200}+\dfrac{1}{10\dfrac{5000\times27}{5000+27}}} \\\Rightarrow\;C_{\text{éq}}&=&9.96\cdot10^{-11}F \end{array}$
Calcul de la capacité $C_{3}$
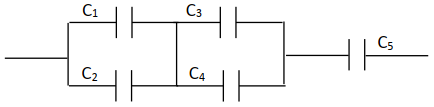
$\begin{array}{rcl} \dfrac{1}{C_{\text{éq}}}&=&\dfrac{1}{C_{1}+C_{2}}+\dfrac{1}{C_{3}+C_{4}}+\dfrac{1}{C_{5}}\\\Rightarrow\dfrac{1}{C_{3}+C_{4}}&=&\dfrac{1}{C_{\text{éq}}}-\dfrac{1}{C_{1}+C_{2}}-\dfrac{1}{C_{5}}\\\Rightarrow\;C_{3}+C_{4}&=&\dfrac{\left(C_{1}+C_{2}\right)C_{5}C_{\text{éq}}}{\left(C_{1}+C_{2}\right)C_{5}-C_{\text{éq}}C_{5}-C_{\text{éq}}\left(C_{1}+C_{2}\right)}\\\Rightarrow\;C_{3}&=&\dfrac{\left(C_{1}+C_{2}+C_{5}\right)C_{\text{éq}}}{\left(C_{1}+C_{2}\right)C_{5}-C_{\text{éq}\left(C_{1}+C_{2}\right)}}-C_{4}\\\Rightarrow\;C_{3}&=&\dfrac{(100+100+1000)\times155}{(100+100)\times1000-155\times1000-155(100+100)}-470\\\Rightarrow\;C_{3}&=&2.21\mu\cdot F \end{array}$
Exercice 3
I. Calcul de :
1. La surface des armatures.
$\begin{array}{rcl} \Rightarrow\;C&=&\dfrac{\varepsilon S}{e}\\&=&\dfrac{\varepsilon_{r}\varepsilon_{0}S}{e}\\\Rightarrow\;S&=&\dfrac{Ce}{\varepsilon_{r}\varepsilon_{0}}\\&=&\dfrac{0.12\cdot10^{-6}\times0.2\cdot10^{-3}}{5\times8.84\cdot 10^{-12}}\\\Rightarrow\;S&=&0.54\,m^{2} \end{array}$
2. La charge du condensateur soumis à la tension de service.
$\begin{array}{rcl} Q&=&CU_{S}\\&=&0.12\cdot10^{-6}\times100\\\Rightarrow\;Q&=&12\cdot10^{-6}C \end{array}$
3. L'énergie emmagasinée.
$\begin{array}{rcl} E&=&\dfrac{1}{2}\dfrac{Q^{2}}{C}\\&=&\dfrac{1}{2}\dfrac{\left(12\cdot10^{-6}\right)^{2}}{0.12\cdot10^{-6}}\\\Rightarrow\;E&=&5.0\cdot10^{-4}J \end{array}$
II. Calcul de :
1. La charge total de l'ensemble formé par les deux condensateurs.
$Q=12\cdot10^{-6}C$
2. La tension commune aux deux condensateurs en régime permanent.
$U=100\,V$
3. L'énergie emmagasinée par le montage
$E=5.0\cdot10^{-4}J$
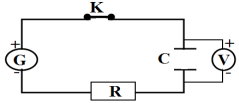
Exercice 4
1. Schéma du montage permettant de suivre l'évolution de $U_{c}$ au cours du temps

2. Détermination graphique de la capacité $C$ du condensateur.
$\begin{array}{rcl} E&=&\dfrac{1}{2}\dfrac{q^{2}}{C}\\\text{ or }q&=&It\\\Rightarrow\;E&=&\dfrac{1}{2}\dfrac{I^{2}}{C}t^{2}\dfrac{1}{2}\dfrac{I^{2}}{C}\\&=&\dfrac{\Delta E}{\Delta t^{2}}\\\Rightarrow\;C&=&\dfrac{I^{2}\Delta t^{2}}{2\Delta E}\\&=&\dfrac{\left(50\cdot10^{-6}\right)^{2}\times(100-0)}{2\times\left(1.25\cdot10^{-2}-0\right)}\\\Rightarrow\;C&=&10^{-5}F \end{array}$
3. Calcul de la permittivité relative du condensateur.
$\begin{array}{rcl} C&=&\dfrac{\varepsilon S}{e}\\&=&\dfrac{\varepsilon_{r}\varepsilon_{0}S}{e}\\\Rightarrow\varepsilon_{r}&=&\dfrac{Ce}{S\varepsilon_{0}}\\&=&\dfrac{10^{-5}\times0.1\cdot10^{-3}}{1\times8.85\cdot10^{-12}}\\\Rightarrow\varepsilon_{r}&=&113 \end{array}$
Exercice 5
1.La capacité C du condensateur en $\mu F$
$\begin{array}{rcl} C&=&\dfrac{Q}{U}\\\text{ or }Q&=&I_{0}t\\\Rightarrow\;C&=&\dfrac{I_{0}t}{U}\\&=&\dfrac{0.30\cdot10^{-3}\times8}{12}\\&=&2\cdot10^{-4}F\\\Rightarrow\;C&=&200\mu F \end{array}$
2. Valeur de la charge $q$ portée par son armature positive
$\begin{array}{rcl} q&=&CU\\&=&150\cdot10^{-3}\times500\\\Rightarrow\;q&=&75.0\,C \end{array}$
L'énergie $E$ stockée par ce condensateur
$\begin{array}{rcl} E&=&\dfrac{1}{2}CU^{2}\\&=&\dfrac{1}{2}\times150\cdot10^{-3}\times500^{2}\\\Rightarrow\;E&=&18.8\cdot10^{3}J \end{array}$
Exercice 6
1. Calcul de la valeur de l'énergie $W_{1}$ emmagasinée par $C_{1}$
$\begin{array}{rcl} W_{1}&=&\dfrac{1}{2}C_{1}U_{1}^{2}\\&=&\dfrac{1}{2}\times470\cdot10^{-6}\times24^{2}\\\Rightarrow\;W_{1}&=&0.14J \end{array}$
2. La valeur de l'énergie $W_{2}$ emmagasinée par $C_{2}.$
$\begin{array}{rcl} W_{2}&=&\dfrac{1}{2}C_{1}U_{2}^{2}\\&=&\dfrac{1}{2}\times1000\cdot10^{-6}\times0^{2}\\\Rightarrow\;W_{2}&=&0\cdot J \end{array}$
3. Détermination de la valeur de la tension $U$ aux bornes des deux condensateurs
$U=24\,V$
4. Calcul de la valeur de l'énergie $W_{12}$ emmagasinée
$\begin{array}{rcl} W_{12}&=&\dfrac{C_{1}C_{2}}{C_{1}+C_{2}}U^{2}\\&=&\dfrac{470\cdot10^{-6}\times1000\cdot10^{-6}}{470\cdot10^{-6}+1000\cdot10^{6}}\times24^{2}\\\Rightarrow\;W_{12}&=&0.18\,J \end{array}$
5. Comparons $W_{12}$ avec $W_{1}+W_{2}$ et donnons une explication au résultat.
$W_{12}=.18\,J$
$W_{1}=0.14\,J$
$\begin{array}{rcl} W_{1}+W_{2}&=&0.14+0\\\Rightarrow\;W_{1}+W_{2}&=&0.14 \end{array}$
$W_{12}\succ W_{1}+W_{2}$
Le condensateur $C_{2}$ n'était pas totalement déchargé
Exercice 7 : Charge d'un condensateur à courant constant
1. Rappel de l'expression de la charge $Q(i\;,\ t)$ et les unités utilisées.
$Q=it$ avec $i$ en ampères, $t$ en secondes et $Q$ en coulombs
2. Rappel de l'expression de la tension $Q(C\;,\ U)$ et les unités utilisées.
$Q=CU$ avec $C$ en farads, $U$ en vols et $Q$ en coulombs
3. Détermination de la charge $Q$ portée par une armature du condensateur à l'instant $t=t_{1}$
$\begin{array}{rcl} Q&=&It_{1}\\&=&250\cdot10^{-6}\times7\times60\\\Rightarrow\;Q&=&0.105\,C \end{array}$
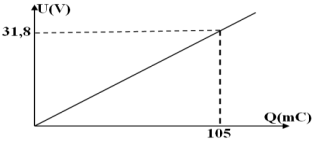
4.Tracé de la courbe $U(Q)$

5. Déduction de la capacité $C$ du condensateur.
$\begin{array}{rcl}C&=&\dfrac{\Delta Q}{\Delta U}\\&=&\dfrac{(105-0)\cdot10^{-3}}{31.8-0}\\\Rightarrow\;C&=&3.30\cdot10^{-3}F \end{array}$
6. Calcul de l'énergie $W$ emmagasinée par le condensateur à la l'instant $t_{1}$
$\begin{array}{rcl} W&=&\dfrac{1}{2}QU\\&=&\dfrac{1}{2}\times0.105\times31.8\\\Rightarrow\;W&=&1.67\,J \end{array}$
Exercice 8: Association de condensateurs
1. Expression de la capacité équivalente $C_{S}$
$\begin{array}{rcl} C_{S}&=&\dfrac{C_{1}C_{2}}{C_{1}+C_{2}}\\&=&\dfrac{2.2\times3.3}{2.2+3.3}\\\Rightarrow\;C_{S}&=&1.32\;m\cdot F \end{array}$
2. Expression de la capacité équivalente $C_{p}$
$\begin{array}{rcl} C_{p}&=&C_{1}+C_{2}\\&=&2.2+3.3\\\Rightarrow\;C_{p}&=&5.5\,m\cdot F \end{array}$
3. Détermination de la charge $Q_{1}$ portée par une armature de ce condensateur.
$\begin{array}{rcl} Q_{1}&=&C_{1}U\\&=&2200\cdot10^{-6}\times30\\\Rightarrow\;Q_{1}&=&66\cdot10^{-3}C \end{array}$
4. Détermination de la charge portée par l'ensemble.
$\begin{array}{rcl} Q&=&Q_{1}\\\Rightarrow\;Q&=&66\cdot10^{-3}C \end{array}$
5. Déduction de la tension U' aux bornes de l'ensemble.
$\begin{array}{rcl} U'&=&\dfrac{Q}{C_{p}}\\&=&\dfrac{66\cdot10^{-3}}{5.5\cdot10^{-3}}\\\Rightarrow\;U^{'}&=&12\,V \end{array}$
Exercice 9 : Association de condensateurs en parallèle
1.1. La capacité équivalente du groupe de deux condensateurs
$\begin{array}{rcl} C_{EQ}&=&C_{1}+C_{2}\\&=&6\cdot10^{-6}+10\cdot10^{-3}\\\Rightarrow\;C_{EQ}&=&10^{-2}F \end{array}$
1.2. La $d\cdot d\cdot p\cdot$ aux bornes des condensateurs en parallèle
$\begin{array}{rcl} U&=&\dfrac{Q}{C}\\&=&\dfrac{200\cdot10^{-3}}{10^{-2}}\\\Rightarrow\;U&=&20\,V \end{array}$
1.3 Charge accumulée sur les armatures du condensateur de $6\,m\cdot F$
$\begin{array}{rcl} Q&=&CU\\&=&6\cdot10^{-3}\times 20\\\Rightarrow\;Q&=&12\cdot10^{-2}C \end{array}$
1.4. Charge accumulée sur les armatures du condensateur de $10\,m\cdot F$
$\begin{array}{rcl} Q&=&CU\\&=&10\cdot10^{-3}\times20\\\Rightarrow\;Q&=&2.0\cdot10^{-1}C \end{array}$
2.1 Détermination des charges $Q_{1}$ et $Q_{2}$
$\begin{array}{rcl} Q_{1}&=&C_{1}U\\&=&3.3\cdot10^{-3}\times20\\\Rightarrow\;Q_{1}&=&6.6\cdot10^{-2}C \end{array}$
$\begin{array}{rcl} Q_{2}&=&C_{2}U'\\&=&2200\cdot10^{-6}\times10\\\Rightarrow\;Q_{2}&=&22\cdot10^{-3}C \end{array}$
2.2 La charge $Q$ portée par l'ensemble
$\begin{array}{rcl} Q&=&Q_{1}+Q_{2}\\&=&6.6\cdot10^{-2}+2.2\cdot10^{-2}\\\Rightarrow\;Q&=&8.8\cdot10^{-2}C\end{array}$
2.3. Déduction de la tension $U"$ aux bornes de l'ensemble
$\begin{array}{rcl} U"&=&\dfrac{Q}{C_{1}+C_{2}}\\&=&\dfrac{8.8\cdot10^{-2}}{3.3\cdot10^{-2}+2200\cdot10^{-6}}\\\Rightarrow\;U"&=&1.6\,V \end{array}$
Exercice 10 : Association de condensateurs en série.
1. Détermination de la capacité équivalente $C_{EQ}.$
$\begin{array}{rcl} C_{EQ}&=&\dfrac{C_{1}C_{2}}{C_{1}+C_{2}}\\&=&\dfrac{20\times33}{20+33}\\\Rightarrow\;C_{EQ}&=&12\,n\cdot F \end{array}$
2. Calcul de la charge $Q$ portée par la capacité équivalente.
$\begin{array}{rcl} Q&=&C_{EQ}U\\&=&12\cdot10^{-9}\times20\\\Rightarrow\;Q&=&24\cdot10^{-8}C \end{array}$
3. La charge $q$ portée par un condensateur.
$\begin{array}{rcl} q&=&Q\\\Rightarrow\;q&=&24\cdot10^{-8}C \end{array}$
4. Déduction de la tension $U_{1}$ aux bornes de $C_{1}$ et de la tension $U_{2}$ aux bornes de $C_{2}.$
$\begin{array}{rcl} U_{1}&=&\dfrac{q}{C_{1}}\\&=&\dfrac{24\cdot10^{-8}}{20\cdot10^{-9}}\\\Rightarrow\;U_{1}&=&12\,V \end{array}$
$\begin{array}{rcl} U_{2}&=&\dfrac{q}{C_{2}}\\&=&\dfrac{24\cdot10^{-8}}{33\cdot10^{-9}}\\\Rightarrow\;U_{2}&=&7.3\,V \end{array}$
5. Calcul de l'énergie $W$ emmagasinée par l'ensemble.
$\begin{array}{rcl} W&=&\dfrac{1}{2}QU\dfrac{1}{2}\times24\cdot10^{-8}\times20\\\Rightarrow\;W&=&24\cdot10^{-7}J \end{array}$
Exercice 11
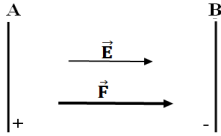
1. Les caractéristiques de la force électrique $\overrightarrow{F}$ qui s'exerce sur chaque ion entre les deux plaques $A$ et $B$
Direction et sens (voir figure)
Intensité :
$\begin{array}{rcl} F&=&2eE\\&=&2e\dfrac{U_{AB}}{d}\\&=&2\times1.6\cdot10^{-19}\times\dfrac{4\cdot10^{4}}{0.10}\\\Rightarrow\;F&=&12.8\cdot10^{-14}N\end{array}$
2. Evaluons le rapport $\dfrac{P}{f'}$
$\begin{array}{rcl} \dfrac{F}{P}&=&\dfrac{F}{mg}\\&=&\dfrac{12.8\cdot10^{-14}}{1.16\cdot10^{-25}\times10}\\\Rightarrow\dfrac{F}{P}&=&11\cdot10^{10}\\\Rightarrow\;F&\succ& P \end{array}$
Le poids $P$ est négligeable devant la force $F$
3. Calcul de l'énergie cinétique de chaque ion arrivant en $B'$, en Joules et en électronvolts :
3.1. Par utilisation du théorème de l'énergie cinétique.
$\begin{array}{rcl} E_{C_{B}}-E_{C_{A}}&=&W\left(\overrightarrow{F}\right)\\\Rightarrow\;E_{C_{B}}&=&W\left(\overrightarrow{F}\right)+E_{C_{A}}\\&=&2eU_{AB}+\dfrac{1}{2}mV_{A}^{2}\\&=&2\times1.6\cdot10^{-19}\times4\cdot10^{4}+\dfrac{1}{2}\times1.16\cdot10^{-25}\times\left(10^{5}\right)^{2}\\\Rightarrow\;E_{C_{B}}&=&1.34\cdot10^{-14}J\\\Rightarrow\;E_{C_{B}}&=&84\,e\cdot V \end{array}$
3.2 Par utilisation de la conversation de l'énergie total $\left(E_{c}+E_{p}\right)$ de l'ion,
$\begin{array}{rcl} E_{m_{B}}&=&E_{m_{B}}\\\Rightarrow\;E_{C_{B}}+E_{P_{B}}&=&E_{C_{A}}+E_{P_{A}}\\\Rightarrow\;E_{C_{B}}+2eV_{B}&=&\dfrac{1}{2}mV_{A}^{2}+2eV_{A}\\\Rightarrow\;E_{C_{B}}&=&2e\left(V_{A}-V_{B}\right)+\dfrac{1}{2}mV_{A}^{2}\\\Rightarrow\;E_{C_{B}}&=&2eU_{AB}+\dfrac{1}{2}mV_{A}^{2}\\&=&2\times1.6\cdot10^{-19}\times4\cdot10^{4}+\dfrac{1}{2}\times1.16\cdot10^{-25}\times\left(10^{5}\right)^{2}\\\Rightarrow\;E_{C_{B}}&=&1.34\cdot10^{-14}\\\Rightarrow\;E_{C_{B}}&=&84\;e\,V \end{array}$
3.3 Déduction de la vitesse d'un ion en $B'$
$\begin{array}{rcl} E_{C_{B}}&=&\dfrac{1}{2}mV_{B}^{2}\\\Rightarrow\;V_{B}&=&\sqrt{\dfrac{2E_{C_{B}}}{m}}\\&=&\dfrac{2\times1.34\cdot10^{5}m\cdot s^{-1}}{1.16\cdot10^{-25}}\\\Rightarrow\;V_{B}&=&4.8\cdot10^{5}m\cdot s \end{array}$
Exercice 12
a. La tension entre ses bomes à la fin de la charge
$\begin{array}{rlc} U_{C}&=&E\\\Rightarrow\;U_{C}&=&6\;V \end{array}$
b. L'énergie emmagasinée par ce condensateur
$\begin{array}{rcl} W&=&\dfrac{1}{2}C_{1}U_{c}^{2}\\&=&\dfrac{1}{2}\times2\cdot10^{-6}\times6^{2}\\\Rightarrow\;W&=&36\cdot10^{-6}J \end{array}$
2. a. Le courant s'annule dans le circuit formé par $C_{1}$ et $C_{2}$ lorsque la tension du condensateur $C_{2}$ est égale à la
tension du condensateur $C_{1}$
b. Calcul des charges électriques finales de chacun de deux condensateurs.
$\begin{array}{rcl} Q_{1}&=&C_{1}U_{c}\\&=&2\cdot10^{-6}\times6\\\Rightarrow\;Q_{1}&=&12\cdot10^{-6}C \end{array}$
$\begin{array}{rcl} Q_{2}&=&C_{2}U_{C}\\&=&1\cdot10^{-6}\times6\\\Rightarrow\;Q_{2}&=&6\cdot10^{-6}C\end{array}$
3. La capacité du condensateur équivalent à l'association de condensateurs $C_{1}$ et $C_{2}$ dans chacun des cas
a. Les condensateurs $C_{1}$ et $C_{2}$ sont branchés en série
$\begin{array}{rcl} C_{EQ}&=&\dfrac{C_{1}C_{2}}{C_{1}+C_{2}}\\&=&\dfrac{2\times1}{2+1}\\\Rightarrow\;C_{EQ}&=&0.7\mu\,F \end{array}$
b. Les condensateurs $C_{1}$ et $C_{2}$ sont branchés en parallèle
$\begin{array}{rcl} C_{EQ}&=&C_{1}+C_{2}\\&=&2+1\\\Rightarrow\;C_{EQ}&=&3\mu\,F \end{array}$

Commentaires
Ntsoumou (non vérifié)
sam, 06/01/2024 - 16:29
Permalien
Je vais bien mais j'ai un
Ajouter un commentaire