Exercice dénombrement - TL
Classe:
Terminale
Exercice 1
On a représenté sur le diagramme ci-dessous un ensemble et deux sous-ensembles de (Chaque élément est représenté par une lettre de l'alphabet).
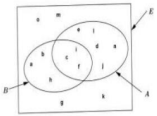
1. Énumérer les éléments de chacun des ensembles suivants : $A$, $B$, $A\cup B$, $A\cap B$, $A/B$, $B/A$, $A\Delta B$, $E\left(A\cap B\right)$ et $E\left(A\cup B\right)$
2. En déduire : card $(A)$, card $(B)$, card $(A \cup B)$ et card $\left(A \cap B\right).$
3. Établir la relation liant card $(A)$, card $(B)$, card $(A\cup B)$ et card $\left(A\cap\right)$ puis vérifier la.
Exercice 2
Dans une classe de $30$ élèves, $20$ parlent français, $12$ parlent anglais et $10$ parlent français et anglais.
1. Combien d'élèves parlent anglais uniquement.
2. Combien d'élèves parlent français ou anglais ?
3. Combien d'élèves ne parlent ni français ni anglais ?
Exercice 3
Dans une classe de $35$ élèves il y a $23$ sénégalais, $18$ maliens et $10$ sénégalo – maliens.
Déterminer
1. Le nombre d'élèves ayant uniquement la nationalité sénégalaise.
2. Le nombre d'élèves ayant uniquement la nationalité malienne.
3. Le nombre d'élèves ayant soit la nationalité malienne, soit la nationalité sénégalaise.
4. Déterminer le nombre d'élèves qui n'ont ni la nationalité sénégalaise ni la nationalité malienne.
5. On choisit successivement 3 élèves pour représenter la classe à l'assemblée de l'école.
a. Calculer le nombre de choix possibles
b. Déterminer le nombre de possibilités d'avoir :
1 élève de nationalité sénégalaise uniquement, $1$ élève de nationalité malienne uniquement et $1$
élève qui est ni sénégalais, ni malien.
$2$ élèves de nationalité sénégalaise uniquement au moins
un élève de nationalité sénégalo –malienne.
Exercice 4
Déterminer le nombre d'anagramme des mots suivants : ATHENA, ZEYNAB, ABABACAR MISSISSIPI, RAMADAN, NDOGOU, ANAGRAMME, DENOMBREMENT
MATHEMATIQUES, ANTICONSTITUTIONNELLEMENT
2. Souadou entre dans un restaurant où l'on propose $7$ entrées, $5$ places de résistance et $8$ dessers.
Combien de menu peut-elle composé sachant qu'un menu est composé d'une entrée, d'un plat de résistance et d'un dessers.
3. Combien de menus différents peut-on composer si on a le choix entre $3$ entrées, $2$ plats et $4$ desserts ?
4. Une femme a dans sa garde-robe $4$ jupes, $5$ chemisiers et $3$ vestes.
Elle choisit au hasard une jupe, un chemisier et une veste. De combien de façons différentes peut-elle s'habiller ?
Exercice 5
Dans une classe de $45$ élèves, $17$ parlent Wolof ; $15$ parlent Pulaar ; $8$ parlent Diola ; 5 parlent Pulaar et Diola ; $8$ parlent Wolof et Pulaar ; $6$ parlent Wolof et Diola et 4$4$ parlent les $3$ langues.
1. Traduire ces données sous forme schéma (diagramme de Venn).
2. Combien d'élèves parlent au plus une des $3$ langues ?
3. Combien d'élèves parlent au moins une des $3$ langues ?
B : $\text{ card } A(\cup B\cap C)=\text{ card } (A)+ \text{ card } (B)+\text{ card }(C)−\text{ card }\left(A\cap B\right)−\text{ card }\left(A\cap C\right)- \text{ card } \left(B\cap C\right)+ \text{ card }\left(A\cap B\cap C\right)$
Exercice 6
Une valise contient $3$ écharpes rouges, $4$ noires, $2$ vertes.
On tire successivement avec remise quatre écharpes de la valise.
Les écharpes sont supposées indiscernables au touché.
Calculer le cardinal des ensembles suivants :
$A$ "avoir des écharpes de la même couleur"
$B$ "avoir une écharpe rouge, $2$ noirs et une verte dans cet ordre."
$C$ "avoir au moins une écharpe noire" ; $D$ "avoir au plus trois écharpes noires"
$E$ " avoir autant d'écharper rouges que d'écharper vertes" Commentaire : pour cette question « $E$ » , au besoin, se rapprocher d'un spécialiste
$F$ " avoir trois écharpes de couleurs différentes "
Exercice 7
Dans un centre de rechercher, on se propose de former, pour une expérience, une équipe de $4$ chercheurs choisis parmi un effectif de $10$ personnes dont $4$ femmes :
1. Combien d'équipes différentes peut-on ainsi constituer ?
2. Combien d'équipes différentes peut-on constituer
A : « si les $4$ chercheurs sont des femmes ? »
B : « si un chercheur et un seul doit être une femme »
C : « si un chercheur au moins doit être une femme »
Exercice 8
Une urne contient $5$ billets de $F$ ; $3$ billets de $F$ et billets de $F.$
On tire au hasard et simultanément $3$ billets de l'urne.
1. Combien y a-t-il de tirages distincts ?
2. Combien y a-t-il de tirages dont la valeur est $300\,F$ ?
3. Combien y a-t-il de tirages dont la valeur est supérieure ou égale à $450\,F$ ?
Exercice 9
Une urne contient $2$ boules rouges portant le chiffre boules noires portant le chiffre et $6$ boules vertes portant le chiffre.
On extrait successivement $3$ boules de l'urne en remettant la boule tirée dans l'urne après chaque tirage.
1. Définir l'univers $\Omega$ associé à cette épreuve.
Déterminer son cardinal.
2. Quelle est la probabilité des événements suivants :
A : « obtenir exactement une boule portant le chiffre $0$ »
B : « obtenir exactement $2$ boules portant le chiffre $1$ »
C : « obtenir $3$ boules portant le même chiffre »
D : « obtenir exactement $2$ vertes »
Exercice 10
Un sac contient trois jetons blancs et deux jetons noirs.
On tire simultanément trois jetons de l'urne.
Combien y a t il de tirages contenant :
1. Un jeton noir et un seul.
2. $2$ jetons noirs.
3. aucun jeton noir
4. au moins un jeton noir.
Exercice 11
1. Combien de mots de $4$ lettres distinctes peut-on former avec les lettres du mot conflit.
2. Combien de ces mots ne contiennent que des consonnes ?
3. Combien de ces mots contiennent $2$ consonnes et $2$ voyelles ?
4. Combien de ces mots contiennent la lettre $T$ ?
5. Combien de ces mots finissent par la lettre $T$ ?
6. Combien de ces mots commencent par une voyelle ?
Exercice 12
A l'aide de $6$ chiffres $1$, $2$, $3$, $4$, $5$ et $6$, combien peut-on écrire
1. de nombres de $3$ chiffres
2. de nombres de $3$ chiffres distincts
3. de nombres de $6$ chiffres distincts
Exercice 13
Dans un centre de rechercher, on se propose de former, pour une expérience, une équipe de $4$ chercheurs choisis parmi un effectif de $10$ personnes dont $4$ femmes :
1. Combien d'équipes différentes peut-on constituer ainsi ?
2. Combien d'équipes différentes peut-on constituer si les $4$ chercheurs sont des femmes ?
3. Combien d'équipes différentes peut-on constituer si un chercheur et un seul doit être une femme
4. Combien d'équipes différentes peut-on constituer si un chercheur au moins doit être une femme
Exercice 14
Une urne contient $3$ boules vertes et $7$ boules jaunes.
On tire successivement avec remise $4$ boules de l'urne.
Déterminer le nombre de triages comportant :
1.a. $4$ jaunes
b. $4$ vertes
c. $3$ jaunes et une verte dans cet ordre
d. $3$ jaunes et une verte
e. $2$ jaunes et $2$ vertes dans cet ordre
f. $2$ jaunes et $2$ vertes
2. Reprendre la question $1.$ dans le cas où les $4$ boules sont tirées successivement sans remise
Exercice 15
Une urne contient $5$ jetons vertes numérotes de $1$ à $5$ et $4$ jetons rouges numérotes de $1$ à $4$
1. On tire simultanément $3$ jeton de l'urne.
Combien y a t il de tirages contenant :
a. $3$ jetons de la même couleur ?
b. contenant le vert numéro $1$ et le rouge numéro $1$ ?
c. un seul jeton portant le numéro $1$ ?
d. exactement un jeton vert et un jeton numéro $1$ ?
2. On tire successivement sans remise $3$ jetons de l'urne.
a. Combien y a-t-il de tirages possibles.
b. Combien y a-t-il de tirages contenant $1$ rouge et $2$ vert dans cet ordre.
c. Combien y a-t-il de tirages contenant $1$ rouge et $2$ verts dans un ordre quelconque.
Exercice 16
Un bana-bana présente en vrac un lot de $13$ paires de chaussures .
Les chaussures ne se différencient que par leurs pointures ou par le fait qu'elles sont soit du pied droit soit du pied gauche .
Parmi les $13$ paires, il y a $4$ paires de la pointure $40$, $6$ paires de la pointure $41$ et $3$ paires de la pointure $42.$
Un client choisit au hasard $2$ chaussures dans le tas des $26$ chaussures .
1. Combien y a-t-il de possibilités pour que les deux chaussures soient de pointures différentes ?
2. Combien y a-t-il de possibilités pour que les deux chaussures soient de la même pointure ?
3. Combien y a-t-il de possibilités pour que les deux chaussures soient du même pied ?
4. Combien y a-t-il de possibilités pour que les deux chaussures soient de pieds différents ?
Exercice 17
Une urne contient $12$ boules numérotées : $5$ noires $(5N)$, $3$ blanches $(3B)$, $4$ rouges $(4R).$
1. On tire simultanément $5$ boules.
a. Combien y a-t-il de tirages possibles ?
b. Combien y a-t-il de tirages comportant $2N$ et $3B$ ?
c. Combien y a-t-il de triages comportant $2R$ ; $1N$ et $2B$ ?
2. On tire successivement et sans remise $5$ boules.
Répondre aux questions précédentes.
3. On tire successivement et avec remise $5$ boules.
Répondre aux questions précédentes
Exercice 18
Un jury est composé de $7$ membres tirés au sort parmi $12$ hommes et $9$ femmes .
1. Combien de jurys peut-on former ayant $3$ femmes et $4$ hommes ?
2. Combien de jurys peut-on former ayant au moins une femme ?
3. Combien de jurys peut-on former sachant que Mademoiselle $X$ refuse de siéger avec Monsieur $Y$ ?
Exercice 19
Une urne contient $7$ boules blanches numérotées de $1$ ; $2$ ; $3$ ; $4$ ; $5$ ; $6$ ; $7$ et $8$ boules rouges numérotées de $8$ ; $9$ ; $10$ ; $11$ ; $12$ ; $13$ ; $14$ ; $15.$
Sachant que l'on tire simultanément $5$ boules de l'urne, déterminer :
1. le nombre de tirages possibles.
2. le nombre de tirages contenant $5$ boules de même couleur.
3. le nombre de tirages contenant au moins $3$ boules rouges.
4. le nombre de tirages contenant $5$ boules dont les numéros sont pairs.
5. le nombre de tirages contenant $5$ boules dont les numéros sont inférieurs ou égaux à $9.$
6. le nombre de tirages contenant au plus $2$ boules blanches
Exercice 20
Dans un jeu de $32$ cartes, on tire simultanément $8$ cartes, qui constituent une main.
1. Calculer le nombre de possibilités.
2. Dénombrer les mains qui contiennent :
a. exactement un sac
b. aucun as
c. au moins un as
d. exactement $2$ cœurs et $3$ piques
e. exactement $2$ cœurs, $3$ piques et un trèfle
f. exactement $2$ cœurs et $2$ dames
g. $4$ cartes de même valeur
Exercice 21
On jette simultanément $3$ dés identiques dont les faces sont numérotées de $1$ à $6$ et on note les résultats possibles.
1. Calculer le nombre de possibilités ?
2. Calculer le nombre de façon d'obtenir :
a. le même numéro
b. des numéros différents
c. les numéro $5$ exactement une fois
Exercice 22
Un sac contient $15$ boules dont $3$ blanches numérotées de $1$ à $3$, $5$ rouges de $1$ à $5$, $7$ jaunes de $1$ à $7.$
1. On tire simultanément $3$ boules du sac.
Calculer le nombre de tirages comprenant :
a. $3$ boules de même couleur.
b. au moins une boule jaune.
c. Exactement une boule jaune et exactement une boule numérotée $2.$
2. On tire successivement avec remise $3$ boules du sac.
Calculer le nombre de tirage comprenant.
a. Une boule au premier tirage.
b. Exactement $2$ boules jaunes cote à cote.
Exercice 23
Un panier contient $30$ poissons dont $10$ Meureug, $12$ tass et $8$ sompatt.
On suppose que les poissons sont indiscernables au toucher. Maguette Mbodji, pour préparer son « thiébou-dieun » , tire successivement et sans remise $3$ poissons du panier.
1. Combien y a-t-il de tirages possibles ?
2. Combien de tirages comportent exactement deux Meureug ?
3. Combien de tirages ne comportent aucun tass ?
4. Combien de tirages comportent au moins un tass ?
5. Combien de tirages comportent trois poissons de la même espèce ?
Exercice 24
Une classe de $30$ élèves, $18$ filles et $12$ garçons, doit élire un comité comprenant un président, un trésorier et un secrétaire (sachant qu'il n'y a ni cumul ni discrimination).
1. Combien de comités peut-on ainsi constituer ?
2. Quel est le nombre de comités comprenant l'élève $X$ ?
3. Quel est le nombre de comités pour lesquels le président est une fille et le secrétaire un garçon ?
4. Sachant que le président est un garçon, le secrétaire une fille, et que monsieur $X$ ne veut pas faire partie du même comité que mademoiselle $Y$, quel est le nombre de comités possibles ?
Exercice 25
Au poker, on donne à chacun des $4$ joueurs une « main » de $5$ cartes d'un jeu de $32$ cartes.
Chaque carte a une valeur (par ordre croissant : $7$, $8$, $9$, $10$, valet, dame, roi, as) et une couleur (trèfle, carreau, cœur, pique).
1. Combien y a-t-il de mains différentes ?
2. Combien y a-t-il de « quinte flush » (mains formées de $5$ cartes consécutives de la même couleur) ?
3. Combien y a-t-il de « couleurs » (mains formées de $5$ cartes non consécutives de la même couleur) ?
4. Combien y a-t-il de « carrés » (mains contenant $4$ cartes de la même valeur, $4$ as ou $4$ rois par exemple) ?
5. Combien y a-t-il de « fulls » c'est-à-dire de mains formées de cartes de la même valeur ( $3$ as par exemple) et de $2$ autres cartes de la même valeur ($2$ rois par exemple) ?
6. Combien y a-t-il de « quinté » (mains formées de $5$ cartes de valeurs consécutives pas nécessairement de même couleur) ?
7. Combien y a-t-il de « brelans » (mains où figurent $3$ cartes de la même valeur) ?
8. Combien y a-t-il de « simple paire » (mains contenant $2$ cartes de la même valeur et de couleurs différentes) ?
Exercice 26
Les numéros d'un réseau téléphonique sont tous formés de $6$ chiffres choisis parmi les chiffres : $0$, $1$, $2$, $3$, $4$, $5$, $6$, $7$, $8$, $9.$
Exemples de numéros théoriquement acceptés : $000000$ ; $982517$ ; $022233$ ; $\ldots\ldots\ldots\ldots$
Calculer le cardinal des ensembles suivants :
$\Omega$ : : la capacité théorique du réseau
A : « ensemble des numéros composés de $6$ chiffres distincts »
B : « ensemble des numéros composés de $6$ chiffres identiques »
C : « ensemble des numéros ne contenant aucun $0$ »
D : « ensemble des numéros contenant exactement un $0$ »
E : « ensemble des numéros contenant au moins un $0$ »
F : « ensemble des numéros contenant au moins deux $0$ »
G : « ensemble des numéros pairs, chaque numéro étant strictement inférieur à $600000$ »
H : « ensemble des numéros commençant par un chiffre pair et finissant par un chiffre impair strictement
inférieur à $7.$ »
Exercice 27
Au loto, une grille simple est un choix de $6$ numéros parmi $1$, $2$, $\ldots\ldots\ldots\ldots$, $48$, $49.$
1. Quel est le nombre total de grilles que l'on peut jouer ?
2. Une grille gagnante ayant été déterminée, calculer, parmi toutes les grilles possibles, le nombre d'entre elles comportant exactement bons numéros pour $n=5$ ; $n=4$ ; $n=3$
Exercice 28
Pour ouvrir son téléphone portable, G-Maleye doit composer un code secret de quatre chiffres sur un clavier numérique de dix chiffres : $0$ ; $1$ ; $2$ ; $3$ ; $4$ ; $5$ ; $6$ ; $7$ ; $8$ ; $9.$
1. Déterminer le nombre de codes possibles.
2. Combien y a-t-il de codes commençant par $2$ ?
3. Combien y a-t-il de codes ne contenant pas $0$ ?
Exercice 29
La confédération africaine de football décide de classer par ordre les $3$ meilleurs joueurs africains de l'année $2019$, parmi un groupe de $22$ joueurs choisis par les journalistes sportifs.
Parmi les $22$ joueurs figurent trois sénégalais : Sadio Mane, Kalidou Koulibaly et Mbaye Niang.
1. Calculer le nombre de classements possibles ;
2. Calculer le nombre de classements tels que :
a. les trois joueurs choisis soient tous des sénégalais ;
b. Sadio Mane soit élu meilleur joueur parmi les $3$ joueurs choisis ;
c. Koulibaly figure parmi les $3$ joueurs choisis ;
d. Seul le $1^{er}$ des trois joueurs choisis est sénégalais
e. Il y a au moins un sénégalais parmi les trois joueurs choisis.
(NB : $II$ n'y a pas de possibilité d'ex-aequo).
Exercice 30
Les numéros de téléphones du réseau téléphonique sénégalais ont $7$ chiffres.
1. Quel est la capacité théorique de ce réseau ?
2. Sachant que les numéros de téléphones fixes de la région de Dakar commencent par le chiffre $8$, déterminer le nombre de numéros de téléphones fixes que peut compter la région de Dakar.
3. Quel est le nombre de numéros de téléphones ayant exactement $2$ chiffres identiques ?
4. Quel est le nombre de numéros de téléphones ayant exactement $2$ fois $2$ chiffres identiques, les autres étant distincts.
5. Quel est le nombre de numéros de téléphones ayant $3$ chiffres identiques, les autres étant distinct
Exercice 31
Une pièce de théâtre est jouée par un groupe de $10$ acteurs (et actrices) désignés au hasard dans un troupe de $25$ artistes comportant $14$ femmes et $11$ hommes dont DIEK et NGOR.
1. De combien de façons peut-on choisir le groupe de $10$ acteurs pour jouer la pièce ?
2. Combien y a-t-il de groupes comprenant seulement $3$ hommes ?
3. Combien y a-t-il de groupes comprenant autant de femmes que d'hommes ?
4. Combien y a-t-il de groupes comprenant au moins $2$ femmes ?
5. Combien y a-t-il de groupes comprenant NGOR ?
6. Combien y a-t-il de groupes comprenant NGOR et DIEK ?
7. Combien y a-t-il de groupes comprenant NGOR ou DIEK ?
8. Combien y a-t-il de groupe comprenant ni NGOR ni DIEK ?
9. Combien y a-t-il de groupes comprenant NGOR et pas DIEK ?

Ajouter un commentaire