Concours miss sciences - 2nd 2013
Exercice 1
Pour chacun des énoncés ci-dessous, entoure la bonne réponse.
$\begin{array}{|c|c|c|c|c|} \hline N^{°}&\text{ Enoncés}&\text{Réponses proposées }&\\ \hline 1&\text{Si }ABCD\text{ est un rectangle, alorsdans}&&&\\&\text{lerepère}\left(A\;,\overrightarrow{AB}\;,\overrightarrow{AC}\right)&(0,1)&(1,1)&(1.0)\\ &\text{le point }C\text{ a pour coordonnées}&&&\\ \hline 2&\text{Si }\cos(x)=\dfrac{-\sqrt{2}}{2}&&&\\ &\text{ et }\sin(x)=\dfrac{\sqrt{2}}{2}\text{alors, dans }&\dfrac{-\pi}{4}&\dfrac{3\pi}{4}&\dfrac{5\pi}{4}\\ &[-\pi\ ;\ \pi[\;,x\text{ est égal à}&&&\\ \hline 3&\cos\left(\dfrac{\pi}{2}+x\right)\text{ est égale à }&\sin x&-\cos x&-\sin x\\ \hline 4. &\text{ La mesure principale de }&&&\\ &\dfrac{17\pi}{5}\text{ dans }[-\pi\ ;\ \pi[\text{est égale à }-\dfrac{-3\pi}{5}&\dfrac{-3\pi}{5}&\dfrac{3\pi}{5}&\dfrac{2\pi}{5}\\ \hline 5&\cos\left(\dfrac{7\pi}{5}\right)\text{ est }&\text{ négatif }&\text{ nul }&\text{psitif}\\ \hline\end{array}$
$\begin{array}{|c|c|c|c|} \hline 6.&\text{« Le cercle a une infinité }&\text{vrai }&\text{faux }\\ &\text{d’axes de symétrie » }&&\\ \hline 7.&\text{« Dans l’espace quand deux droites sont }&&\\ &\text{perpendiculaires tout droite perpendiculaire à l’une }&\text{vrai}&\text{faux}\\ &\text{est parallèle à l’autre » est un énoncé }&&\\ \hline 8&« \vec{u}(2\;,1)\text{ est un vecteur directeur de (D) :}&\text{vrai }&\text{ faux }\\ &2x+y-1=0 » \text{ est un énoncé }&&\\ \hline 9&« \text{Si }x=-2\text{alors }x^{2}-7x-18=0»&\text{vrai }&\text{faux }\\ &\text{est un énoncé }&&\\ \hline 10&« \text{Si } x^{2}-7x-18=0\text{alors }x=-2»&\text{vrai }&\text{faux }\\ &\text{est un énoncé }&&\\ \hline \end{array}$
Exercice 2
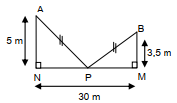
Un martin-pêcheur est perché sur une branche $B.$
Il aperçoit un poisson $P$ dans la rivière et plonge directement sur lui, remonte en ligne droite pour se poser sur une autre branche $A.$
La distance parcourue pour atteindre le poisson est égale à celle parcourue pour se poser sur la branche $A.$
Voir la figure ci-dessous.
Calculer la distance $MP.$
Exercice 3
Soit les réels $a$ et $c$ tels que :
$1<a\leq 2\;,-3\leq c\leq -1$ et $y=a-ac+\dfrac{2}{a}.$
Déterminer un encadrement de $Y.$
Exercice 4
On donne la figure ci-contre où $ABCD$ est un rectangle,$M\in[DC]$ et $N\in[BC].$
L'unité de mesure est le centimètre.
La figure ne sera pas reproduite.
On donne : $AB=10\ ;\ BC=6\ ;\ DM=x\ :\ BN=\dfrac{x}{2}.$
1. Démontrer que le triangle $NCM$ existe si$0\leq x<10.$
2. Déterminer l'ensemble des valeurs de $x$ pour que l'aire du triangle $MCN$
soit inférieure ou égale au quart de l'aire de $ABCD.$

Ajouter un commentaire