Vous êtes ici

Systèmes d'équations linéaires - 2nd L

Classe:

Terminale

1. Généralités

a. définition

On appelle système de deux équations linéaires à deux inconnues tout système qui peut se mettre sous forme :

$\left\lbrace\begin{array}{rcl} ax+by&=&c\\ a'x+b'y&=&c' \end{array}\right.$ où

$a\;,b\;,c\;,c\;,a'\;,b'\;,c'$ sont deux réels donnés.

Une solution d'un tel système est un couple

$(x\ ;\ y)$ tels que

$(x\ ;\ )$ soit solution de chacune des deux équations.

Résoudre un système c'est déterminer tous les couples solutions du système.

Exemple ;

$\left\lbrace\begin{array}{rcl} 2x+3y&=&11\\ 3x-5y&=& \end{array}\right.$ est un système linéaire. Le couple

$(4\ ;\ 1)$ est une solution de ce système.

b. Interprétation graphique

Le plan est muni d'un repère

$\left(O\ .\ \vec{i}\;,\vec{j}\right)$

Soit le système

$(S)\left\lbrace\begin{array}{rc} ax+by&=&c\\\quad (1) a'x+b'y&=&c'\quad (2) \end{array}\right.$ où

$a$ et

$b$ d'une part,

$a'$ et

$b'$ d'autre part ne sont pas simultanément nuls.

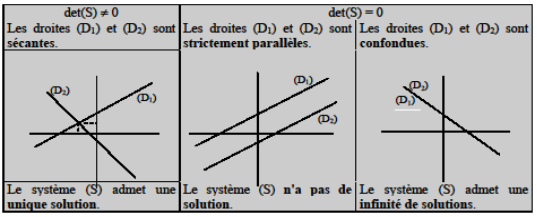
Les équations

$(1)$ et

$(2)$ du système sont les équations de deux droites

$\left(D_{1}\right)$ et

$\left(D_{2}\right)$

Dire qu'un couple

$(x\;,y)$ est solution du système

$(S)$ revient donc à dire que le point

$M$ de coordonnées

$(x\ ;\ y)$ est un point d'intersection des deux droites.

2. Résolution des systèmes

Soit

$(S)$ le

$\left\lbrace\begin{array}{rcl} ax+by&=&c\\ a'x+b'y&=&c' \end{array}\right.$

On appelle déterminant de

$(S)$ le nombre réel noté

$d$ et

$(S)$ défini par

$d$ et

$(S)=ab'-a'b$

Le tableau ci-dessous regroupe les possibles :

5. Comment résoudre un problème ?

Pour résoudre un problème, on peut procéder suit :

$-\$ d'abord, faire le choix des inconnues ;

$-\$ ensuite, traduire les énoncés du problème à des équations du premier degré à deux inconnues ;

$-\$ en outre, former un système d'équations à partir des deux équations trouvées ;

$-\$ en fin résoudre ce système par la méthode de votre choix, si la méthode n'est pas indiquée.

Exemples :

Problèmes :

II. Système d'inéquations du première

1. Définition :

$\ast\$ Inéquation du premier degré à deux inconnues :

On appelle inéquation du premier degré à deux inconnues

$x$ et

$y$ toute inéquation qui peut se ramener sous la forme :

$ax+by+c\leq 0(\text{ ou }>0\text{ ou }\geq 0\text{ ou }<0)$

Exemples :

$\ast\$ Système d'inéquations du premier degré à deux inconnues :

On appelle système de deux ou trois inéquations du premier degré à deux inconnues

$x$ et

$y$ , tout système se ramenant à :

$\left\lbrace\begin{array}{rcl} ax+by+c&\leq&0 (\text{ ou }>0\text{ ou }\geq 0\text{ ou }<0)\text{ ou bien}\\ a'x+b'y+c'&<&0(\text{ ou }\geq 0\text{ ou }<0\text{ ou }\leq) \end{array}\right.$

$\left\lbrace\begin{array}{rcl} ax+by+c&>&(\text{ ou }\geq 0\text{ ou }<0\text{ ou }\leq 0)\\ a'x+b'y+c'&\geq&0(\text{ ou }\geq 0\text{ ou }\leq0\text{ ou }>0)\\ a"x+b"y+c"&<&0(\text{ ou }\geq 0\text{ ou }>0\text{ ou }\leq 0) \end{array}\right.$

Exemples :

2. Région du plan :

Propriétés :

Toute droite

$(\Delta)$ d'équation :

$ax+by+c$ divise le plan en deux demi-plans ouverts :

$-\$ pour tout point

$M(x\ ;\ )$ de l'un des demi-plans, on a :

$ax+by+c>0$ ;

$-\$ pour tout point

$M(x\ ;\ y)$ de l'autre demi-plan, on a :

$ax+by+c<0$

$\begin{array}{|c|c|c|c|c|c|c|} \hline &&&&&&\\ \hline &&&&&&\\ \hline &&&&&&\\ \hline &&&&&&\\ \hline &&&&&&\\ \hline &&&&&&\\ \hline \end{array}$

Exemple :

Construire la droite

$(\Delta)$ d'équation :

$2x+y-4=0$ dans un repère orthogonal

$(O\;,\ I\;, J)$

3. Comment résoudre une inéquation ?

Pour résoudre une inéquation du premier degré à deux inconnues

$x$ et

$y$ , on peut procéder comme suit :

$\ast\$ on trace la droite

$(D)$ ou

$(\Delta)$ d'équation :

$ax+by+c=0$ dans un repère orthogonal

$(O\;, I\;, J)$

$\ast\$ on détermine le demi-plan solution en choisissant un point de coordonnées

$(x\ ;\ y)$ qui n'est pas sur la droite tracée et on teste l'inéquation :

$ax+by+c\leq 0(\text{ ou }>0\text{ ou }\geq 0\text{ ou }<0)$

par les cordonnées de ce point. Et pour cela, on peut rencontrer un des deux cas :

$-$ si l'inéquation est vérifiée, alors les solutions sont les couples

$(x\ ;\ y)$ coordonnées des points situés dans ce demi-plan ;

$-\$ si l'inéquation n'est pas vérifiée, alors les solutions sont les couples

$(x\ ;\ )$ coordonnées des points situés dans l'autre demi-plan.

Exemples :

4. Comment résoudre un système d'inéquations ?

Résoudre un système d'inéquations revient à déterminer l'ensemble des points de coordonnées

$(x\ ;\ y)$ qui vérifient à la fois les deux ou bien les trois inéquations du système.

Autrement dit, résoudre un système d'inéquations c'est déterminer le demi-plan solution ou bien une partie qui est solution du système.

Exemples :

NB :

$\ast\$ Tout nombre réel négatif est toujours plus petit que nombre réel zéro :

$-5<0$ vraie ;

$-2\leq 0$ vraie ;

$-7\geq 0$ fausse ;

$-20000>0$ fausse ;

$\ast\$ Tout nombre réel positif est toujours plus grand que nombre réel zéro :

$-2\geq 0$ vraie ;

$1>0$ vraie ;

$14\leq 0$ fausse ;

$\sqrt{2}<0$ fausse.

Série d'exercices :

Exercice 1 :

Résoudre chacun des systèmes suivants par la méthode indiquée :

$\left\lbrace\begin{array}{rcl} x-y&=&\dfrac{3}{4}\\ 5x+2y&=&3 \end{array}\right.$ ;

$\left\lbrace\begin{array}{rcl} 2x-y&=&5\\ x-2y&=&3 \end{array}\right.$ ;

$\left\lbrace\begin{array}{rcl} 2x-3y&=&1\\ x+y&=&-4 \end{array}\right.$ ;

$\left\lbrace\begin{array}{rcl} 3x-y+2&=&0\\ 3x-y-1&=&0 \end{array}\right.$ ;

$\left\lbrace\begin{array}{rcl} 2y+x&=&5\\ -y+7&=&4 \end{array}\right.$ ;

$\left\lbrace\begin{array}{rcl} 3x-y&=&2\\ 2x-y&=&1 \end{array}\right.$ ;

$\left\lbrace\begin{array}{rcl} x+y&=&3\\ -y+4&=&x-2 \end{array}\right.$ ;

$\left\lbrace\begin{array}{rcl} x-y&=&5\\ x+2y&=&4 \end{array}\right.$ ;

$\left\lbrace\begin{array}{rcl} x-3y&=&11\\ 2x-y&=&8 \end{array}\right.$ ;

$\left\lbrace\begin{array}{rcl} -4x+y&=&2\\ 3x-y&=&-4 \end{array}\right.$ ;

$\left\lbrace\begin{array}{rcl} 2x-y&=&3\\ 3x-y&=&5 \end{array}\right.$ ;

$\left\lbrace\begin{array}{rcl} 3x-2y&=&5\\ 2x+y&=&1 \end{array}\right.$ ;

$\left\lbrace\begin{array}{rcl} \dfrac{x}{2}+\dfrac{y}{3}&=&7\\ \dfrac{x}{3}+\dfrac{y}{2}&=&8 \end{array}\right.$

$\left\lbrace\begin{array}{rcl} \dfrac{x}{6}+\dfrac{y}{5}&=&5\\ \dfrac{2x}{3}-\dfrac{y}{2}&=&8 \end{array}\right.$

$\left\lbrace\begin{array}{rcl} \dfrac{3}{2}x+\dfrac{5}{4}&=&11\\ x+2y&=&11 \end{array}\right.$

$\left\lbrace\begin{array}{rcl} x\sqrt{2}-5y\sqrt{3}&=&17\\ x\sqrt{6}+y&=&\sqrt{3} \end{array}\right.$

$\left\lbrace\begin{array}{rcl} 2x-y-4&=&0\\ x+5y-13&=&0\\ -3x+2y+5&=&0 \end{array}\right.$ ;

$\left\lbrace\begin{array}{rcl} -x+y-3&=&0\\ -2x+2y+1&=&0\\ 3x-2y-4&=&0 \end{array}\right.$

1. méthode de substitution :

$a. \ ;\ b.\ ;\ c$ et

$d.$

2. méthode d'addition :

$e. \ ;\ f.\ ;\ h.\ ;\ q$ et

$r$

3. méthode graphique :

$i$ ;

$j$ ;

$k$ et

$l$ $

4. méthode de CRAMER :

$m$ ;

$n$ ;

$o$ ;

$p$ ;

$q$ rt

$r$

Exercice 2 :

Le périmètre d'un rectangle est

$220m.$

Sa la largeur a

$100$ de moins que sa longueur.

Quelles sont ses dimensions ?

Exercice 3 : Une salle de théâtre compte 400 places. Les « parterres » sont à

$1500\,F$ et les « balcons » à

$1200\,F.$

La recette quand la salle est pleine est

$534000.$

Combien y-a-t-il de « parterres » et de « balcons » ?

Exercice 3 :

Une boite contient

$10$ billles.

Les unes sont rouges et les autres bleues.

On ajoute 3 billes et 2 billes rouges.

Il y a alors deux fois plus de billes bleues que de billes rouges.

Combien y-a-t-il de billes de chaque couleur dans la boite ?

Exercice 4 :

Résoudre graphiquement chacun des systèmes suivants :

$\left\lbrace\begin{array}{rcl} 2x-y+3\leq 0\\ y-2x+1\leq0 \end{array}\right.$ ;

$\left\lbrace\begin{array}{rcl} 2x+3y\geq 0\\ x-2y+1<0 \end{array}\right.$ ;

$\left\lbrace\begin{array}{rcl} x-y+3\leq 0\\ 2x+y-1\leq 0 \end{array}\right.$ ;

$\left\lbrace\begin{array}{rcl} 4x+y-5> 0\\ 2x+y-5<0 \end{array}\right.$ ;

$\left\lbrace\begin{array}{rcl} x-y+3\leq 0\\ 2x+y-1\leq 0 \end{array}\right.$ ;

$\left\lbrace\begin{array}{rcl} x+y-2<0\\ x+2y<-2 \end{array}\right.$ ;

$\left\lbrace\begin{array}{rcl} y&<&3\\ x&>&-2\\ y&>&2x-1 \end{array}\right.$ ;

$\left\lbrace\begin{array}{rcl} x&>&0\\ x\&geq&0\\ y&>&-x+3.5 \end{array}\right.$

Exercice 5 :

Un collectionneur veut acheter, pour remplir un rayon de sa bibliothèque, des livres de

$4\,cm$ d'épaisseur et des livres de

$5\,cm$ d'épaisseur.

Il souhaite avoir au moins

$7$ livres de la première sorte, au moins

$8$ livres de la deuxième sorte et la longueur du rayon ainsi constituée soit strictement comprise entre

$60\,cm$ et

$80\,cm$

1. Traduire ces données par un système d'inéquation.

2. Déterminer tous les couples d'entiers répondant aux exigences précisées ci-dessus.

Ajouter un commentaire

form.antibot { display: none !important; } You must have JavaScript enabled to use this form.

Vous êtes ici

Systèmes d'équations linéaires - 2nd L

Formulaire de recherche

1. Généralités

a. définition

II. Système d'inéquations du première

1. Définition :

2. Région du plan :

Propriétés :

4. Comment résoudre un système d'inéquations ?

Série d'exercices :

Exercice 1 :

Exercice 2 :

Exercice 3 :

Exercice 4 :

Exercice 5 :

Ajouter un commentaire

Plain text