Bac Mathématiques TS1 2024 - Epreuves 1er groupe
Exercice 1
Dans l'espace, on considère $8$ points $O$, $A$, $B$, $C$, $D$, $E$, $F$ et $G$ tels que $OABCGDEF$ soit un cube d'arête une unité.
l'espace est muni du repère orthonormé $\left(O\ ;\ \overrightarrow{OA}\;,\overrightarrow{OC}\;,\overrightarrow{OG}\right)$
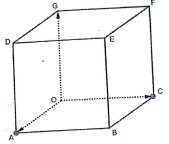
1. Donner les coordonnées des points $A$, $C$, $G$ et $E$
2.a. Déterminer les coordonnées du vecteur $\overrightarrow{AG}\Lambda\overrightarrow{AC}$
b. En déduire une équation cartésienne du plan $(AGG)$
4. Déterminer les coordonnées du points $I$ intersection de la droite $(OE)$ et du plan $(AGC)$
5. Calculer alors le volume du tétraèdre $OAGC.$
6. On note $(P)$ et $\left(P'\right)$ respectivement les plans médiateurs de $[AC]$ et de $[CG]$ et on note $s$ et $s'$ les réflexions par rapport respectivement aux plans $(P)$ et $\left(P'\right)$
a. Déterminer $\left(s'°s\right)(A)$
b. Démontrer que $s'°s$ est une rotation d'axe $(OI)$
c. Soit $\theta$ son angle, déterminer $|\theta|$
Exercice 2
1. On considère les nombres $\alpha=57370$ et $b=104275$
a. Déterminer le $PGCD$ de $a$ et $b$
b. L'équation $ax+by=5$ admet-elle des solutions dans $\mathbb{Z}\times\mathbb{Z}$ ?
2. Soit $(E)$ d'équation : $11474x+20855y=1$
a. Vérifier que le couple $(3059-1683)$ est solution de l'équation $(E)$
b. Résoudre dans $\mathbb{Z}\times\mathbb{Z}$ l'équation $(E)$
c. En déduire les solutions dans $\mathbb{Z}\times\mathbb{Z}$ de l'équation $ax+by=5$
3. Pour chacune des propositions suivantes, dire si elle est vraie ou fausse :
$P_{_{1}}$ : Dans la base $P$ où $p$ est un entier naturel supérieur ou égal à $2$, $p-1$ est un chiffre.
$P_{2}$ : Dans la base $7,8$ est un chiffre.
$P_{3}$ : Dans la base $16$, $E$ est un chiffre.
$P_{4}$ : Dans la base $8$, les chiffres sont : $0\ ;\ 1\ ;\ 2\ ;\ 3\ ;\ 4\ ;\ 5\ ;\ 6\ ;\ 7$
4. Deux commerçantes Anta et fatou se rendent au marché pour acheter des articles.
Un article coûte $5$ francs l'unité.
Anta et fatou disposent respectivement d'un montant de $S_{1}$ et de $S_{2}$ en francs.
On sait que $S_{1}=1x00y2$ en base huit, et fatou $S_{2}=x1y003$ en base sept.
a. Donner, en fonction de $x$ et $y$ les expressions se $S_{1}$ et de $S_{2}$ en base dix.
b. Déterminer les chiffres $x$ et $y$ pour que chacune des deux commerçantes puisse dépenser tout montant à sa disposition.
c. En déduire le nombre d'articles que chacune d'elles pourra acheter.
Problème
Soit $n$ un entier naturel.
On considère la fonction $f_{n}$ définie par :
$f_{n}(x)=\mathrm{e}^{\left(n+\dfrac{1}{2}\right)}x\times\sqrt{2-\mathrm{e}^{x}}$
On note $C_{n}$ la courbe représentative de $f_{n}$ dans le plan muni d'un repère orthonormé $\left(O\ ;\ \vec{i}\;,\vec{j}\right)$, l'unité graphique est $4\,cm$
1. Déterminer le domaine de définition de $f_{n}$, puis calculer les limites aux bornes de cet ensemble.
2. Montrer que toutes les courbes $C_{n}$ passent par deux points fixes que l'on déterminera.
3. Étudier les positions relatives des courbes $C_{n+1}$ et $C_{n}$ pour $n\in\mathbb{N}$
4. Étudier les variations de $f_{n}.$
5. Montrer que $f_{n}$ admet un maximum $a_{n}$ puis exprimer $a_{n}$ en fonction de $n.$
6. Dresser le tableau de variations de $f_{n}$
7. Tracer les courbes $C_{1}$, $C_{2}$ et $C_{3}$
8. Soient $\left(U_{n}\right)$ et $\left(V_{n}\right)$ les suites définies pour tout $n\in\mathbb{N}$ par : $U_{n}=\ln\left(\dfrac{2n+1}{n+1}\right)$ et $V_{n}=f_{n}\left(U_{n}\right).$
a. Déterminer la limite de $U_{n}$
b. Calculer la limite de $\ln\left(V_{n}\right)$ et en déduire celle de $V_{n}$
Partie B
Soit $\varphi$ la fonction définie sur $]0\;,2[$ par : $\varphi(t)=\sqrt{t(2-t)}$
1. Montrer que $\varphi\left(\mathrm{e}^{t}\right)=f°(t)$
2. Soit $g$ fonction définie sur l'intervalle $]0\;,2[$ par : $g(t)=\ln\left(\varphi(t)\right)$
a. Soit $\beta$ un réel de l'intervalle $]0\;,2[$
Résoudre dans $]0\;,2[$ l'équation $g(t)$ - $g(Q)$
b. En déduire que la courbe $C_{g}$ de la fonction $g$ dans le repère $\left(O\ ;\ \vec{i}\;,\vec{j}\right)$ est invariante par une transformation que l'on déterminera.
3. Étudier les variations de $g.$
4. Tracer $C_{g}.$
5. Soit $h$ les restrictions de $g$ à l'intervalle $]0\;,1]$
a. Montrer que $h$ est une bijection de $]0\;,1]$ sur un intervalle $J$ que l'on précisera
b. Donner l'expression $h^{-1}(t)$ de $h^{-1}$ pour tout élément $t$ de $J$
6. Soit $G=h^{-1}°G;$
Déterminer le domaine de $G$, puis l'expression $G(t)$ de $G$ pour tout $t$ de l'intervalle
Partie C
Pour tout entier naturel $n$, on considère la fonction $\varphi_{n}$ définie sur $[0\;,2]$ par : $$\varphi_{0}(t)=\sqrt{t(2-t)}\text{ et }\forall n\in\mathbb{N}^{\ast}\quad\forall_{n}(t)=t^{n}\sqrt{t(2-t)}$$
On désigne par $F_{n}$ la fonction définie de l'intervalle $\left[-\dfrac{-\pi}{2}\;,\dfrac{\pi}{2}\right]$ dans $\mathbb{R}$ par $$F_{n}(\theta)=\int_{0}^{1+\sin\theta}\varphi_{n}(t)dt$$
1. Justifier l'existence de $F_{n}(\theta)$ pour tout entier naturel $n$ et pour tout réel $\theta$ de l'intervalle $[-\dfrac{\pi}{2}\;,\dfrac{\pi}{2}]$
2.Déterminer que pour tout entier naturel $n$, $F_{n}$ est dérivable sur l'intervalle $[-\dfrac{\pi}{2}\;,\dfrac{\pi}{2}]$ et déterminer sa fonction dérivée $F^{'}_{n}.$
3. déterminer $F_{0}(\theta)$ et $F_{1}(\theta)$ pour $\theta\in[-\dfrac{\pi}{2}\;,\dfrac{\pi}{2}]$
4. Calculer l'aire $\mathbb{A}$ du domaine plan $\mathbb{D}$ définie par : $$D={M(t\;,y)\text{ tel que }0\leq t\leq 1\text{ et }\varphi_{1}(t)\leq y\leq\varphi_{o}(t)}$
5. Dans le plan muni du repère orthonormé $\left(O\ ;\ \vec{i}\;,\vec{j}\right)$, on note de la fonction $\varphi_{0}$ et $\left(\Gamma_{0}^{'}\right)I$ courbe d'équation : $y=-\varphi_{0}(t)$
On pose $(\Gamma)=\left(\Gamma_{0}'\right)\cup\left(\Gamma_{0}'\right)$
Montre que $(\Gamma)$ est un cercle dont on e le centre et le rayon.

Ajouter un commentaire