Suite numerique
1. METHODE DE RAISONNEMENT PAR RECURRENCE
Exemple 1 : Soit à démontrer la propriété : $(1) 1^{2} + 2^{2}+ 3^{2}+ …..+ n^{2}=\frac{n(n+1)(2n+1)}{6} \forall n\in \mathbb{N}$*,
a) Remarquons d’abord que cette propriété est vraie pour n = 1, car alors le membre de gauche est égal à $1^{2} = 1$ et celui de droite à $\frac{1\times{2}\times{3}}{6}=1$.
b) Supposons que la propriété est vraie pour un entier k, c’est-à-dire que : $(2) 1^{2} + 2^{2}+ 3^{2}+ …..+ k^{2} =\frac{k(k+1)(2K+1)}{6}$.
Montrons alors qu’elle est vraie pour $n = k + 1$.
En effet, d’après (2) :
$1^{2}+ 2^{2}+ 3^{2}+ …..+ k^{2}+ (k + 1)^{2} =\frac{k(k+1)(2K+1)}{6}+{(k+1)}^{2}$
$=(k + 1)(\frac{k(2k+1)}{6}+(k+1))=(k+1)(\frac{2k^{2}+7k+6}{6})=(\frac{(k+1)(K+2)(2k+3)}{6}) {(3)}$.
(3) est identique à (1) avec $n = k + 1$.
Ainsi, on a démontré que: (3) Si la propriété est vraie pour n = k, alors elle est vraie pour n = k + 1.
c) Or (1) est vraie pour n = 1, donc d’après (3) avec n = 1 , elle est vraie pour n = 2.
Donc, d’après (3) avec n = 2, elle est vraie pour n = 3.
Donc, d’après (3) avec n = 3, elle est vraie pour n = 4…...
En continuant ce raisonnement, on voit que la propriété (1) est vraie pour tout entier naturel n.
De manière générale, nous admettrons le principe suivant, appelé principe de récurrence :
Soit à démontrer une propriété (Pn) dépendant de l’entier naturel n.
(a) Si on démontre qu’elle est vraie pour une certaine valeur $n = n_{0}$ ,
(b) Et si on démontre que dès qu’elle est vraie pour n = k, alors elle est vraie pour n = k + 1
(c) Alors, on peut conclure qu’elle est vraie pour $n \geq n_{0}$.
Exemple 2: Démontrer que : $\forall {n ≥ 1}$ , 7 divise $2^{n + 1} + 3^{2n ― 1}$.
N.B. On dit que l’entier k divise l’entier n (notation : k | n) si et seulement si: il existe un entier p tel que : $n = k\times{p}$.
(a) pour $n = 1, 2^{2} + 3^{1} = 7 = 7\times{1}$ et $7|7$ ,
donc la propriété est vraie.
(b) Supposons qu’elle est vraie pour n = k, c’est-à-dire que : $7|2^{k+1} + 3^{2k―1}$.
Il existe donc un entier p tel que $2^{k+1}+3^{2k ― 1} = 7p (∗)$.
Alors, $2^{k + 2}+3^{2k + 1} = 2(2^{k + 1}) + 9 × 3^{2k ― 1}$.
D’après (∗), ceci est égal à : $2(7p ― 3^{2k ― 1}) + 9 × 3^{2k―1} = 14p + 7 × 3^{2k―1} = 7 (2p + 3^{2k―1})$.
Donc, $2^{k + 2} + 3^{2k + 1}$ est aussi un multiple de 7.
On en conclut que : $\forall {n ≥ 1}$ , 7 divise $2^{n+1}+3^{2n―1}$ .
Exercices : 1) Démontrer par récurrence les propriétés suivantes :
a)$\forall n\in \mathbb{N}$*, $\sum_{p=n}^{p=1} p.p!=(n+1)!-1$
b)$\forall n\in \mathbb{N}$*,$\sum_{p=0}^{p=n}(2p+1)^{3}(n+1)^{2}(2n^{2}+4n+1)$
c)$\forall n\in \mathbb{N}$*,$\sum_{p=n}^{p=1} p.p(p+1)=\frac{n(n+1)(n+2)}{3}$
d)$\forall n\in \mathbb{N}$*,11 divise $3^{2n+2}+3^{6n+1}$.
2) Démontrer que, si $10^{n+1}$ est divisible par 9, alors ($10^{n+1}+1$) est divisible par 9. Peut-on en conclure que, pour tout n de $\mathbb{N}$, $10^{n+1}$ est divisible par 9 ?
2. GENERALITES SUR LES SUITES
2.1 Définition: Une suite numérique est une fonction u d’une partie A de $\mathbb{N}$ vers $\mathbb{N}$.
$u : A \rightarrow \mathbb{N}(A \subset \mathbb{N})$.
L’image $u(n)$ d’un entier $n\in{A}$ par $u$ est notée $u_n$ (notation indicielle).
La suite elle-même est notée ($u_{n})$ $n\in{A} $.
Remarque :
? Ne pas confondre :
- la suite ($u_{n}$) qui est une application ;
- le terme de rang n, un qui est un réel ;
- {$u_{n}$ , $n\in \mathbb{N}$}, ensemble des valeurs de la suite.
. Certaines suites ne sont définies qu'à partir d'un certain rang, comme par exemple :
$u_{n}=\frac{1}{n}$ définie pour $n \in \mathbb{N}$*. $v_{n}=\sqrt{n-3}$ définie pour $n\geq{3}$.
Notons que le domaine de définition est nécessairement du type $[n_{0},+\infty[$ = ensemble des entiers n tels que $n\geq{n_{0}}$,où $n_{0}\mathbb{N}$.
2.2 Modes de définition d’une suite
Une suite peut être définie de deux manières :
· Suite définie en fonction du rang n (définition explicite) :
Exemple : $u_{n}=\frac{(-1)^{n}}{n}$, pour $n\geq{1}$. On obtient : $u_{1} = - 1$ ; $u_{2} =\frac{1}{2}$; $u_{3} = -\frac{1}{3}$ etc...
Exercice : Calculer les six premiers termes de la suite $(U_n)$ dans chacun des cas suivants :
a) $u_{n} = 2^{n} - 3^{n - 1}$; b) $u_{n} =\frac{(- 1)^{n}}{n}$ ; c) $u_{n} =n\frac{\sqrt{n}}{n+1}$ d) $u_{n}=(-1)^{n}\cos\frac{n\pi}{3}$ .
· Suite définie par une relation de récurrence :
Exemple 1 :$\left\{
\begin{array}{rl}
u_{0} &= 2 \\
u_{n+1}&= U_{n}=u_{n}(1-u_{n})
\end{array}
\right.$
On obtient : $u_{1} = u_{0} (1 -u_{0})=-2 $; $u_{2} =-6 $ ; $u_{3} =-42 $ etc….
Exemple 2 :$\left\{
\begin{array}{rl}
u_{0} &= 2 u_{1}=1 \\
u_{n}&= u_{n-1}+u_{n-2} \forall n\geq 2 & \text{(Suite de FIBONACCI)}
\end{array}
\right.$
On obtient : $u_{2} = 1 + 1 = 2$ ; $u_{3} = 2 + 1 = 3$ ; $u_{4} = 3 + 2 = 5$ ; $u_{5} = 5+3 = 8$ etc….
(Chaque terme est a somme des deux précédents).
Exercice :
1)Calculer les six premiers termes de la suite (un) dans chacun des cas suivants :
a) $u_{0} = 9$ ; $u_{n+1} = f(u_{n})$, avec $f(x) = \frac{2x-5}{x+1}$
b) Pour tout n de $\mathbb{N}$*, $u_{n+1} =2u_{n}+\frac{1}{u_{n-1}}$ Avec $u_{0}=1$ et $u_{1} = 1$.
2) soit $(u_{n})$ la suite définie par : $u_{0}=1$ ; $u_{1}=2$ et $u_{n+2}=5u_{n+1}-6u_{n}$ pour tout $n\geq{0}$.
Démontrer que $u_{n}=2^{n}$
pour tout entier n.
2.3. Sens de variation d’une suite
2.3.1 Définition
Soit $u_{n} n\in{A}$ une suite de nombres réels. On dit que :
La suite ($u_{n}$) est croissante (à partir du rang $n_{0}$) lorsque $u_{n}\leq{u_{n+1}}$ pour tout entier $n\geq{n_{0}}$.
La suite ($u_{n}$) est décroissante (à partir du rang $n_{0}$) lorsque $u_{n}\geq{u_{n+1}}$ pour tout entier $n\geq{n_{0}}$.
La suite ($u_{n}$) est monotone (à partir du rang n_{0}) si elle est croissante ou décroissante (à partir du rang $n_{0}$).
La suite ($u_{n}$) est stationnaire lorsque $u_{n}= u_{n+1}$ pour tout $n\geq{n_{0}}$. (Constante si ($u_{n}$) est définie à partir du rang n0).
N.B. On définit la stricte croissance (ou décroissance) à l'aide de l'inégalité stricte $u_{n}<u_{n+1} (u_{n} > u_{n+1}$).
2.3.2 Méthode
Pour vérifier qu'une suite est croissante (ou décroissante), on calcule, pour tout indice n, labdifférence de deux termes consécutifs $u_{n+1}-u_{n}$. Si on obtient une quantité positive, alors la suite ($u_{n}$) est croissante. Si on obtient une quantité négative, alors la suite ($u_{n}$) est décroissante. Si on obtient une quantité de signe variable alors la suite n'est ni croissante, ni décroissante.
Exemple : $u_{n}=2n+\sin{n}$.
Étudions, pour tout entier n, le signe de la différence de deux termes consécutifs :
$u_{n+1}-u_{n}=2(n+1)+\sin{(n+1)}-2n-\sin{n}=2+\sin{(n+1)}-\sin{n}$
Or $-1\leq\sin{(n+1)}\leq{1}$ et $-1\leq {-\sin{n}}\leq{1}$, donc $-2=\sin{(n+1)}-\sin{n}\leq{2}$,
par conséquent : $u_{n+1}- u_{n} =0$ : la suite ($u_{n}$) est donc croissante.
2.3.3 Cas des suites du type $u_{n}=f(n)$ :
Théorème : Où l'on utilise une fonction associée
Soit ($u_{n}$) la suite définie par $u_{n}=f(n)$ où f est une fonction définie sur un intervalle du type $[a;+\infty[$ où $a \in\mathbb{R}+$.
Si la fonction $f$ est monotone sur $[a ;+\infty[$ alors la suite ($u_{n}$) est monotone sur $[E(a)+1;+\infty[$ et possède le même sens de variation que $f$.
Démonstration :
Supposons f croissante sur $[a ;+\infty[$. (Les autres cas se prouvent de manière analogue)
Pour tout $n\in [E(a)+1;+\infty[$, on a alors : $u_{n+1}-u_{n}=f(n+1)-f(n)>0$
Donc ($u_{n}$) est croissante sur $[E(a)+1;+\infty[$.
Exercice : Etudier le sens de variation de la suite (un) dans chacun des cas suivants :
1) $u_{n}=-3n^{2}+20n+100$ 2) $u_{n}=\frac{-3n+4}{n+2}$ 3) $u_{n} =\frac{(1,1)^{n}}{n}$
4) $u_{n+1} = 3u_{n}-2u_{n} - 1$ ,$ u0 = 1$, $u_{1} = 2$ 5) $2u_{n+1}=u_{n}-u_{n-1}$ , $u_{0}=0$, $u_{1} =-3$.
2.4 Suites bornées
Définition :
On dit que la suite ($u_{n})n\in{A} $
. majorée s’il existe $u_{n}$réel M tel que, pour tout n de A, $u_{n} \leq{M}$.
. minorée s’il existe $u_{n}$ réel m tel que, pour tout n de A, $u_{n}\leq{M}$
. bornée si et seulement si elle est majorée et minorée.
Remarque : La suite ($u_{n}) n\in{A}$ est bornée s’il existe un couple (m, M) de réels tel que, pour tout n de A, on a :$ m\leq{u_{n}}\leq{M}$.
Exemples : 1°) Soit ($u_{n}$) la suite définie par : $u_{n} =\frac{(- 1)^{n}+\sin{n}}{n^{2}}$.
On a $-2\leq (-1)^{n}+\sin{n}\leq{2}$ et $0\leq{\frac{1}{n^{2}}}\leq{1}$ pour $n\geq{1}$. D’où : $- 2 \leq u_{n} \leq 2$. La suite est bornée.
2°) Soit (un) la suite définie par : $u_{n} =\sum_{k=1}^{k=n} \frac{1}{k^{2}}=1+\frac{1}{2^{2}}+...+\frac{1}{n^{2}}$.
Montrons que ($u_{n}$) est majorée par 2.
On peut remarquer que: $\frac{1}{k^{2}}\leq{\frac{1}{k(k-1)}}=\frac{1}{k}-\frac{1}{k-1}$ .
D’où $u_{n} =1+\sum_{k=2}^{k=n} \frac{1}{k^{2}}\leq 1 + \sum_{k=2}^{k=n} (\frac{1}{k-1}-\frac{1}{k})=1+1-\frac{1}{n}=2-\frac{1}{n}<2$.
.
Exercices :
1) Montrer que la suite ($u_{n}) n\in{A}$ est bornée si et seulement si il existe un réel positif A tel que pour tout n de A,
on a : $|u_{n}|\geq{A}$.
2) Soit ($u_{n}$) la suite définie par : $\left\{
\begin{array}{rl}
u_{0} &= 16 \\
u_{n+1}&= \sqrt{U_{n}}
\end{array}
\right.$
Démontrer par récurrence que cette suite est décroissante.
3) Soit la suite ($u_{n}$) définie sur $\mathbb{R}$ par : ($ u_{0}=0$ et pour tout entier naturel n, $u_{n+1} =\sqrt{2+u_{n}}$ ).
a) Calculer les 4 premiers termes de la suite. Donner une valeur approchée à 10- 2 près pour chacun des réels :
$u_{1}$, $u_{2}$ et $u_{3}$.
b) Démontrer que cette suite est strictement monotone.
c) Démontrer que cette suite est majorée par 2.
d) En déduire qu’elle est bornée.
e) Soit la suite ($v_{n}$) définie sur $\mathbb{R}$ par : ( $v_{0}=2$ et pour tout entier naturel n, $v_{n+1}=\sqrt{2+v_{n}}$ ).
Démontrer que cette suite est constante.
4) On considère la suite u définie sur $\mathbb{R}$ par : $u_{n} = 2n +\frac{1}{n}$ .
a) Soit M un réel quelconque. Il existe au moins un entier naturel non nul $n_0$ tel que l’on a : $n_{0} > M$.
Justifier que l’on a alors l’inégalité :$u_{n_{0}} > n_{0}$.
b) En déduire que $u_{n_{0}} > M$, puis que la suite ($u_{n}$) n’est pas majorée.
5) On considère la suite ($u_{n}$) définie sur $\mathbb{N}$ par: $\left\{
\begin{array}{rl}
u_{0} &= 8 ;u_{1} =\frac{11}{2} \\
u_{n+1}&= \frac{3U_{n}-u_{n-1}}{2} \forall n\in \mathbb{N}*
\end{array}
\right.$
a) Calculer les les 4 premiers termes de la suite. b) Démontrer que cette suite est strictement monotone.
c) Montrer par récurrence que :$\forall n\in \mathbb{N}$*, $u_{n}= 3+\frac{5}{2^{n}}$ . d) En déduire que la suite (un) est bornée.
2.3 Suites périodiques
Définition :
Soit p un entier naturel non nul. On dit que la suite ($u_{n}) n\in{A}$ est périodique de période p si, pour tout n de A, on a : $u_{n+p} = u_{n}$.
Exemple : Soit ($u_{n}$) la suite définie sur $\mathbb{N}$ par $u_{n} = (─ 1)^{n}$.
Pour tout entier naturel n, on a $u_{n+2} = u_{n}$. Cette suite est donc périodique, de période 2.
Exercices :
1) Montrer que les suites ($u_{n}$) et ($v_{n}$) suivantes sont périodiques et déterminer leur période.
a)$u_{'n} = \sin{\frac{n\pi}{2}}$ b)$V_{n} = \tan{\frac{n\pi}{3}}$ c) $u_{n}= \cos{\frac{n\pi}{7}}+\sin{\frac{2n\pi}{5}}$ d) $u_{n}= (─ 1)^{n}\cos{\frac{3n\pi}{7}}$ .
2) Soit p un entier strictement positif fixé, E la fonction partie entière, ($u_{n}$) la suite définie par :
$u_{n}= n ─ pE(\frac{n}{p})$.
Démontrer que ($u_{n}$) est périodique.
3) Soit un le chiffre des unités de $n^{2}$. Démontrer que ($u_{n}$) est périodique. Préciser la période.
3. Représentation graphique d’une suite
Définition :
On se place dans un repère ($O,\overrightarrow {i},\overrightarrow{j}$ ). La représentation graphique d'une suite ($u_{n}$) est
l'ensemble des points de coordonnées (n ; $u_{n}$).
Exemple 1 : (Cas d’une suite définie explicitement)
Soit ($u_{n}$) la suite définie par $u_{n}=\frac{1}{n}$ pour n ≥ 1. Sa représentation graphique est l'ensemble des
points isolés (1 ; 1), (2 ;$\frac{1}{2}$), (3 ;$\frac{1}{3}$) etc…
Exemple 2 : (Cas d’une suite récurrente de la forme $u_{n+1} = f(u_{n}))$
Dans ce cas, on ne cherche pas en général à représenter la suite suivant la définition ci-dessus
mais on préfère représenter ses premiers termes sur l’axe des abscisses. Pour ce faire, on suit
les étapes suivantes :
a) On trace la courbe représentative$ C_{f}$ de la fonction f définissant la suite récurrente et de la première bissectrice
d’équation y = x ;
b) On place le premier terme $u_{0} $sur l’axe des abscisses;
c) On utilise $C_{f}$ pour construire $u_{1} = f(u_{0})$ sur l’axe des ordonnées;
d) On reporte $u_{1}$ sur l’axe dse abscisses à l’aide de la première bissectrice;
e) On utilise $C_{f}$ pour construire $u_{2}= f(u_{1}$) sur l’axe des ordonnées;
f) etc...
Voici un exemple de construction avec la suite ($u_{n}$) définie par $u_{0}=─1$ et, pour tout n de $\mathbb{N}$, $u_{n+1} = \sqrt{3u_{n+4}}$ .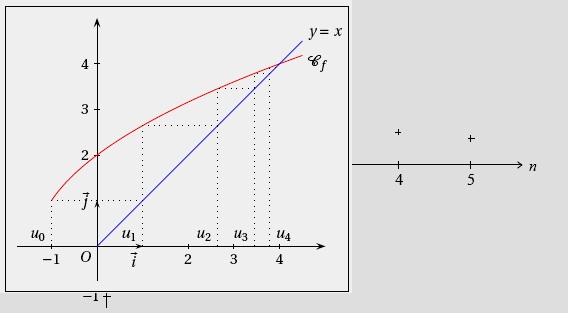
N.B. Ce type de construction permet de faire des conjectures en termes de variation, de comportement à l’infini, etc.
5. SUITES ARITHMETIQUES
5.1 Définition
Une suite ($u_{n}$) est dite arithmétique si l’on passe de chaque terme au suivant en ajoutant toujours le même nombre r : $u_{n+1} = u_n+r$ pour tout indice n.
Ce nombre $r$ s’appelle raison de la suite ($u_{n}$) .
5.2 Méthode
Pour vérifier qu'unesuite est arithmétique,on calcule,pour tout indice n la différence dedeux termes consécutifs $u_{n+1}-u_{n}$ .Sion obtient une quantité constante r alors la suite est arithmétique de raison r. Sion obtient une quantité variable (dépendante de n), alors la suite n'est pas arithmétique.
Exemples : les suites suivantes sont elles arithmétiques ?
1) $u_{n}=3n-2$
Pour tout indice n, on a :
$u_{n+1}-u_{n}=3(n+1)-2-3n+2=3n+3+2-3n+2=3$.La suite ($u_{n}$) est arithmétique de raison r=3.
2) $u_{n}=n^{2}+1$.
Pour tout indice n, on a: $u_{n+1}-u_{n}=(n+1)^{2}+1-(n^{2}+1)=n^{2}+2n+1-n^{2}=2n+1$.
Donc la suite (un) est non arithmétique.
Exercice : Démontrer que trois réels a, b et c sont, dans cet ordre, les termes d’une suite arithmétique si et seulement si l’on a : $b =\frac{a+c}{2}$ (ou encore c ─ b = b ─ a) .
5.3 Propriété caractéristique
Théorème :
La suite ($u_{n}) n\in \mathbb{N}$ est arithmétique de raison r (r réel donné) si et seulement si :
$\forall n\in \mathbb{N}$: $u_{n} = u_{0}+nr$.
On a alors pour tous entiers n et $p : u_{n} = u_{p} + (n ─ p)r$
Démonstration: Par récurrence sur n.
Soit (un)une suite arithmétique de raison r. On considère la propriété $\phi (n)$ définie pour $n\in \mathbb{N}$
par :$ \phi (n) : u_{n} = u_{0} + nr$.
- Si n=0, la propriété est clairement vérifiée donc $\phi (0) $ est vraie.
- Montrons que pour tout $n \in \mathbb{N}: \phi (n)\Leftrightarrow \phi(n+1)$.
Supposons donc, que l'on ait $\phi (n)$, c'est-à-dire : $u_{n} = u_{0}+nr$.
D'après la définition d'une suite arithmétique, on a : $u_{n+1} = u_{n} + r$. Mais comme on a supposé
$\phi(n)$, cela donne : $u_{n+1} = u_{0} + nr +r=u_{0} + (n + 1)r$
On obtient la relation de récurrence au rang n+1, à savoir $\phi (n+1)$.
On a donc bien, pour tout $n\in \mathbb{N} : \phi (n)\Leftrightarrow{ \phi(n+1)}$
- Résumons : si la propriété est vraie à un certain rang, elle est vraie au rang suivant. Comme elle est vraie au rang 0, elle est donc vraie à tout rang. En conclusion, pour tout $n \in \mathbb{N}$, on a :$ u_{n} = u_{0} + nr$.
- En remplaçant n par p, on obtient également : $u_{p} = u_{0} + pr$. Et par différence des deux dernières relations : $u_{n} ─ u_{p}=(n-p)r$. D'où : $u_{n} = u_{p} + (n ─ p)r$.
5.4 Méthode pour calculer un terme quelconque d'une suite arithmétique
.On utilise l'une des relations suivantes : $u_{n} = u_{0} + nr$ ou $u_{n} = u_{p} + (n ─ p)r$.
Exemples : Calculer $u_{26}$ dans les deux cas suivants :
1) $u_{0}=6$ et r=5. $u_{26}=u_{0}+26r=6+26\times{5}=136$.
2) $u_{10}=3$ et r =-2.$ u_{26}=u_{10}+16r=3+16\times{(-2)}=-29$.
5.5 Somme de N termes consécutifs
Théorème :
Cette somme est donnée par la formule : $S=\frac{N(P+D)}{2}$, où N désigne le nombre de termes de
la suite, P, le premier terme et D le dernier terme.
Démonstration : Soit à calculer : S=P+(P+r)+...+(D-r)+D.(somme comprenant N
termes).Cette somme S peut encore s'écrire : $S=D+(D-r)+...+(P+r)+P$. (on a changé
l'ordre des termes). Si bien que, en additionnant :
$2S=(P+D)+(P+D)+... +(P+D)+(P+D)$
(somme comprenant toujours N termes). D'où : $2S=N(P +D)\Rightarrow {S =\frac{N(P+D)}{2}}$ .
5.6 Sens de variation d’une suite arithmétique
Théorème :
Soit (un) est une suite arithmétique de raison r :
.Si r > 0 alors ($u_{n}$) est strictement croissante.
.Si r=0 alors ($u_{n}$) est constante.
.Si r < 0 alors ($u_{n}$) est strictement décroissante.
Démonstration : Comme ($u_{n}$) est arithmétique, on a pour tout entier n : $u_{n+1}-u_{n}=r$
D'où le résultat en utilisant la définition 2.3.1.
Exercices :
1) Soit ($u_{n}$) une suite arithmétique de premier terme $u_{1} = 1$ et de raison r = 6.
Déterminer n de façon que $S_{n} = u-{1} + u_{2} + ....+ u_{n} = 280$. Calculer alors $u_{n}$ pour cette valeur de n.
2) Soit ($u_{n}$) une suite arithmétique. On sait que $u_{11}=121$ et $u_{15}=165$. Calculer r, $u_{0}$, $u_{100}$ puis
$S=u_{0} + u_{1} + ....+ u_{100}$.
3) Soit ($u_{n}$) la suite définie par $u_{n}=5n+4$. Démontrer que ($u_{n}$) est arithmétique et calculer $S=u_{100}+..+u_{200}$.
2) Prouver que si $a^{2}$, $b^{2}$ et $c^{2}$ sont trois termes consécutifs d’une suite arithmétique, il en est de même pour $\frac{a}{b+c}$ ,
$\frac{b}{c+a}$ et$\frac{c}{a+b}$ . La réciproque est-elle vraie ?
4) Calculer les sommes suivantes :
a) $S=1+3+5+7+9+11+..+99$ b) $S=1+2+3+4+...+n$.
5) Soit ($u_{n}) n\in{A}$ une suite arithmétique de raison r. Justifier les propriétés suivantes:
a) Si r est nul, la suite est constante et bornée.
b) Si r est strictement positif, la suite est strictement croissante, minorée et non majorée.
c) Si r est strictement négatif, la suite est strictement décroissante, majorée et non minorée.
6)Déterminer une suite arithmétique de quatre termes, de raison r, dont le produit des termes soit p.
7) Déterminer une suite arithmétique de quatre termes dont la somme soit s et la somme des carrés q.
6. SUITES GEOMETRIQUES
6.1 Définition
Une suite ($u_{n}$) est dite géométrique lorsqu'on passe de chaque terme au suivant en multipliant
toujours par le même nombre $q : u_{n+1}=qu_{n}$.
Ce nombre q s'appelle la raison de la suite ($u_{n}$).
6.2 Méthode
Pour vérifier qu'une suite est géométrique, on peut :
$\rightarrow$ Après s'être assuré que un n'est jamais nul, on calcule, pour tout indice n, le rapport de
deux termes consécutifs $\frac{u_{n+1}}{u_{n}}$.Si on obtient une quantité constante q, alors la suite est
géométrique de raison q. Si on obtient une quantité variable, alors la suite n'est pas
géométrique.
$\rightarrow$ Variante : on montre qu'il existe un réel q tel que, pour tout indice n, on ait $u_{n+1}=qu_{n}$.
Exemples : les suites suivantes sont elles géométriques ?
1) $u_{n}=1,01^{n}$ .
On a, pour tout indice $n : u_{n}\ne{0}$ et $\frac{u_{n+1}}{u_{n}}=\frac{(1,01)^{n+1}}{1,01^{n}}1,01$(constante supérieure ou égale à 1).
Donc ($u_{n}$) est une suite géométrique de raison q=1,01.
1) $u_{n}=n^{2}$ (pour n ≥ 1). On a pour tout indice $n : un\ne{0}$ et $\frac{u_{n+1}}{u_{n}}=\frac{(n+1)^{2}}{n^{2}}$
Cette suite n’est pas géométrique.
Exercice : Démontrer que trois réels a, b et c sont, dans cet ordre, les termes d’une suite géométrique si et
seulement si l’on $a : b^{2}= ac$.
6.3 Propriété caractéristique
Théorème :
La suite ($u_{n})n\in\mathbb{N}$ est géométrique de raison q (q réel donné) si et seulement si :
$\forall n\in \mathbb{N}: u_{n}= q^{n}u_{0}$.
On a alors pour tous entiers n et $p:u_{n} =q^{n─p} u_{p}$.
Démonstration :
. Soit ($u_{n}$) une suite géométrique de raison q. Si q=0 ou si $u_{0}=0$ alors ($u_{n}$) est la suite nulle et
la relation $u_{n}= q^{n}u_{0}$ est triviale.
-Supposons maintenant $q\ne{0}$ et $u_{0}\ne{0}$. Montrons, par récurrence (sur $n\in{\mathbb{N}}$), la propriété :
$p(n) : u_{n} = q^{n} u_{0}$.
─ Si n=0, la propriété est clairement vérifiée donc p(0) est vraie.
─ Montrons que, pour tout $n\in{\mathbb{N}}: P(n)\Rightarrow{(n +1)}$
Supposons donc, que l'on ait P(n), c'est-à-dire : $u_{n}=q^{n} u_{0}$. D'après la définition d'une suite
géométrique, on a : $u_{n+1}=qu_{n}$. D'après l'hypothèse de récurrence p(n), cela donne :
$u_{n+1}=qq^{n}u_{0}=q^{n+1}u_{0}$. On obtient la relation de récurrence au rang n+1, à savoir p(n+1).
On a donc bien pour tout $n\in{\mathbb{N}}:(n)\Rightarrow{p(n+1)}$.
─ En conclusion, pour tout $n\in{\mathbb{N}}$, on a : $u_{n}= q^{n} u_{0}$.
En remplaçant n par p, on obtient également : $u_{p}=q^{n} u_{0}$.
On a donc : $u_{n}q^{p} u_{0} =u_{p}q^{n}u_{0}$. Et comme $u_{0}\ne{0}$ et $q\ne{0}: q^{n-p} u_{p}$.
6.4 Méthode pour calculer un terme quelconque d'une suite arithmétique
$\rightarrow$ On utilise l'une des relations suivantes : $un =q^{n} u_{0}$ ou $u_{n} =q^{n─p} u_{p}$ (pour p ≤ n)
Exemples : Calculer $u_{7}$ dans les deux cas suivants :
1) $u_{0}=\frac{1}{4}$ et q=2. $u_{7}=q^{7} u_{0}=2^{7}\times{\frac{1}{4}}=2^{5}=32$.
2) $u_{4}=81$ et $q=\frac{1}{3}$. . $u_{7}=q^{7─4} u_{4}=q^{3} u_{4}=(\frac{1}{3})^{3}\times{81}=3$.
Exercice : Démontrer que toute suite géométrique ($u_{n}$) peut s'écrire : $u_{n}=a^{n}$ et que, réciproquement, toute
suite définie par une relation du type $u_{n}=a^{n}$ (pour n ≥ 0 et a > 0) est géométrique.
6.5 Somme de N termes consécutifs
Cette somme est donnée par la formule : $S =\frac{P(1 ─ q^{N})}{1─q}$ si $q\ne{1}$, où N=nombre de termes de
la somme, P=premier terme de la somme et q=raison de la suite, et par S = NP si q = 1.
Démonstration :
soit à calculer la somme : $S=P+q^{P}+...+q^{n}_{P}$ (somme comprenant N=n+1 termes)
Remarquons que : $S-qS=P+q^{P}+..+q^{n}_{P}-(q^{P}+q^{2}_{P}+..+q^{n}_{P}+q^{n+1}_{P})=P-P_{q}^{n+1}$
D'où : $S(1-q)=P(1-q^{n+1})$
Si bien que si $q\ne{1} : S =\frac{P(1 ─ q^{N})}{1─q}$
Et si q=1, alors $S=P+q^{P}+...+q^{n}_{P} P+P+...+P=(n+1)P=NP$.
Exercices :
1) Calculer les sommes suivantes :
a) $S=1+2+4+8+16+...+4096$. b) $S = 1+x+x^{2}+…...+x^{n}$. c) $S=1+x^{2}+x^{4}...+x^{2n}$.
2) On considère une suite géométrique de premier terme u_{1}, de n-ième terme $u_{n}$, de raison q, de somme $S_{n}$ :
a) Calculer$u_{n}$ et Sn connaissant $u_{1} = 2$, q = 3, n = 5.
b) Calculer q et $S_{n}$ connaissant $u_{1}=5$, n = 6, $u_{n}= 160$.
c) Calculer $u_{1}$ et $S_{n}$ connaissant q = 3, n =4, $u_{n} = 54$.
d) Calculer $u_{1}$ et $u_{n}$ connaissant $q =\frac{1}{2}$, n =6, S = 63.
3) Soit ($u_{n}$) une suite géométrique. On sait que $u_{8}=\frac{1}{9}$ et $u_{1}=243$. Calculer $q, u_{0}, u_{100}$ puis $S=u_{0}+u_{1}+...+u_{100}$.
4) Soit ($u_{n}$) la suite définie par $u_{n}=5\times{4^{n}}$. Démontrer que ($u_{n}$) est géométrique et calculer $S=u_{100}+...+u_{200}$.
5) On considère les deux suites ($u_{n}$) et ($v_{n}$) définies, pour tout $u_{n}n\in\mathbb{N} u_{n}$, par :
$u_n=\frac{3\times{2^{n}}─4n+3}{2}$ et $v_{n}=\frac{3\times{2^{n}}+4n─3}{2}$
a) Soit ($w_{n}$) la suite définie par$w_{n}=u_{n}+v_{n}$. Démontrer que ($v_{n}$) est une suite géométrique.
b) Soit ($t_{n}$) la suite définie par t_{n}$ =u_{n}-v_{n}$. Démontrer que ($t_{n}$) est une suite arithmétique.
c) Exprimer la somme suivante en fonction de $n : S_{n}=u_{0}+u_{1}+...+u_{n}$.
6) Déterminer 7 termes consécutifs d’une suite géométrique, tels que la somme des 3 premiers termes soit 2 et
celle des 3 derniers 1250.
7) Soit ($u_{n}$) une suite dont les 10 premiers termes sont en progression arithmétique de raison r et, à partir de u10,
les termes sont en progression géométrique de raison q. Soit $u_{1} = 0, u_{16} = ─\frac{1}{27}$ , qr = 1.
a) Calculer q, r, $u_{10}$ et $u_{1} $. b) Calculer $S_{n}$, somme dse n premiers termes pour n ≤ 10, puis pour n > 10.
FORMULAIRE RESUME SUR LES SUITES ARITHMETIQUES ET GEOMETRIQUES
| Suite ($u_{n}$) ;$n\in{\mathbb{N}}$ | suite arithmétique de raison r | suite arithmétique de raison q |
| Définition |
n passe de chaque terme au suivant en ajoutant la même quantité r (raison) : $u_{n+1}= u_{n}+r$ |
On passe de chaque terme au suivant en multipliant par la même quantité q (raison) : $u_{n+1} = qu_{n}$ |
|
Expression d’un terme quelconque $u_{n}$ en fonction d’un précédent $u_{p}$. |
Le nième terme s’obtient à partir du pième en ajoutant n ─ p fois la raison r : $u_{n}=u_{p}+(n ─ p)r$ Et en particulier :$ u_{n}=u_{0}+nr=u_{1}+(n─1)r$ |
Le nième terme s’obtient à partir du pième en ajoutant n ─ p fois la raison r : $u_{n}=u_{p}+(n ─ p)r$ Et en particulier :$ u_{n}=u_{0}+nr=u_{1}+(n─1)r$ Le nième terme s’obtient à partir du pième en multipliant n ─ p fois par la raison q : $u_{n}=q^{n─p)}u_{p}$ Et en particulier : $u_{n}=q^{n}u_{0}=q^{n─1}u_{1}$ |
|
Somme de N termes consécutifs |
$S =\frac{N(P+D)}{2}$ N = nombre de termes de la somme P = premier terme de la somme D = dernier terme de la somme |
$S =\frac{P(1─q^{N})}{1─q}$ (si$ q\ne{1}$, sinon S = NP) N = nombre de termes de la somme |
| Cas particulier |
$S = 1 + 2 + 3 + ….+ n =\frac{n(n+1)}{2}$ (r = 1; P = 1; D = n) |
$S = 1+x+x^{2} ….+x^{n}$ (si $x\in{1}$, sinon S = N + 1) (q = x ; P = 1 ; $D = x^{n}$) |
ONVERGENCE D’UNE SUITE
7.1 Définition : suite convergente
On dit qu'une suite ($u_{n}$) admet une limite l (ou converge vers $l, l\in\mathbb{R}$) lorsque :
Pour tout réel $\epsilon$ strictement positif, il existe un rang N tel que pour tout indice n, on ait :
$n ≥ N\Rightarrow{|u_{n}-l|≤\epsilon}$
On note alors $\lim\limits_{n\to +\infty}u_{n} = l$.
En d'autres termes :Tout intervalle ouvert centré en l contient tous les termes de la suite à
partir d'un certain indice.
Une suite qui a une limite réelle est dite convergente. Elle est dite divergente dans les autres
cas.
7.2 Remarque
Soit ($u_{n}$) une suite du type $u_{n}= f(n)$ : Si $\lim\limits_{n\to +\infty}f(x) = l$, alors $\lim\limits_{n\to +\infty}u_{n} = l$. (Nous admettrons ce
résultat). Les théorèmes vus en Première sur les limites finies de fonctions s'appliquent donc
aux suites de ce type. En conséquence, on récupère dans ce cas tous les théorèmes sur les
opérations algébriques, les limites de référence, ainsi que les théorèmes de comparaison, en
particulier le théorème des "gendarmes".
Exemples :
1°) Soit ($u_{n}$) la suite définie sur $\mathbb{N}$*
par $u_{n} =\frac{2n+3}{n+1}$ . On a $u_{n} = f(n)$ où f est la fonction définie
par $f(x) =\frac{2x+3}{x+1}$ . On sait (cf cours de Première) que :$\lim\limits_{x\to +\infty} \frac{2x+3}{x+1} = \lim\limits_{x\to +\infty} \frac{2x}{x}=2$.
D’où :$\lim\limits_{x\to +\infty} u_{n} = 2$.
2°) Soit ($u_{n}$) la suite définie sur $\mathbb{N}$*
par $u_{n} =\frac{\sin{n}}{n}$ . On a un = f(n) où f est la fonction définie
par $f(x) =\frac{sin{x}}{x}$. On sait que pour tout x strictement positif, $|sin x| ≤ 1$ puis : $0≤\frac{\sin{x}}{x}≤\frac{1}{x}$.
Il résulte du théorème des gendarmes vu en Première sur les fonctions et qui sera rappelé plus
bas, que $\lim\limits_{n\to +\infty}\frac{\sin{x}}{x}=0$ et par conséquent :$\lim\limits_{n\to +\infty} \frac{\sin{n}}{n}= 0$.
3°) Toute suite constante converge vers son premier terme.
7.3 Propriétés des suites convergentes
Nous admettrons toutes les propriétés suivantes:
P.1 : Toute suite convergente est bornée.
Attention! Une suite peut être bornée et divergente (Ex : la suite ($u_{n}$) de terme général
$u_{n} = (─ 1)^{n})$.
On déduit de cette propriété que toute suite non bornée est divergente.
P.2 : Si la suite ($u_{n}$) converge vers l, alors la suite ( |$u_{n}$|) converge vers | l |.
Attention! Il se peut que la suite ( |$u_{n}$|) soit convergente et que la suite ($u_{n}$) soit divergente
(Reprendre l’exemple précédent: $u_{n} = (─ 1)^{n})$.
P.3 : Règles de comparaison
Soient ($u_{n}$) et ($V_{n}$) deux suites définies sur un même ensemble E et l un réel.
a) Si, à partir d’un certain rang, on a : $|u_{n─l} | ≤ v_{n}$ et si l’on a :$\lim\limits_{n\to +\infty} v_{n} = 0$, alors on a :$\lim\limits_{n\to +\infty} u_{n} = l$ .
b) Si, à partir d’un certain rang, on a : $v_{n} ≤ u_{n} ≤ w_{n}$ et si l’on a :$\lim\limits_{n\to +\infty} v_{n}=\lim\limits_{n\to +\infty} w_{n} = l$,
alors on a :$\lim\limits_{n\to +\infty} u_{n} = l$.
Ce dernier résultat est aussi connu sous le nom de théorème des gendarmes.
Exemple : Soit ($u_{n}$) la suite définie par :définie par : $u_{n} =\frac{n}{n^{2}+1}+\frac{1}{n^{2}+2}+...+\frac{1}{n^{2}+n}$ .
Pour tout entier p élément de {1, 2,…..n}, on a : $n^{2}+1≤n^{2}+p ≤n^{2}+n$, d’où :
$\frac{1}{n^{2}+n}≤\frac{1}{n^{2}+p} ≤\frac{1}{n^{2}+1}$.
En sommant ces inégalités pour p allant de 1 à n, on obtient :$\frac{n}{n^{2}+n} ≤ u_{n} ≤\frac{n}{n^{2}+1}$
Or,$\lim\limits_{n\to +\infty} \frac{n}{n^{2}+n}=\lim\limits_{n\to +\infty} \frac{n}{n^{2}-1}=\lim\limits_{n\to +\infty} \frac{1}{n^{2}}= 0$ (Application de la règle analogue sur la
limite d’une fonction rationnelle à l’infini).
On en déduit, en utilisant le théorème des gendarmes, que $\lim\limits_{n\to +\infty} u_{n} = 0$
P.4 : Limite et ordre
Si, à partir d’un certain rang, on a : $u_{n}≤v_{n}$ et si l’on a :$\lim\limits_{n\to +\infty} u_{n} = 1$ et $\lim\limits_{x\to +\infty} u_{n} = K$, alors
on a : $l ≤ k$.
Exercice : En déduire les deux propriétés suivantes :
P.5 : Si, à partir d’un certain rang, on a : $u_{n} ≥ 0$ et si l’on a :$\lim\limits_{n\to +\infty} u_{n} = l$, alors on a l ≥ 0.
Autrement dit : la limite d’une suite convergente de réels positifs est un réel positif ou nul.$\frac{1}{n!}$
Attention : une suite à termes strictement positifs n’a pas nécessairement une limite
strictement positive.
Exemple : $u_{n} =\frac{1}{n}.\forall n\in \mathbb{N}*, u_{n} > 0$, mais $\lim\limits_{n\to +\infty} u_{n} = 0$.
P. 6 : Si, à partir d’un certain rang, on a : $a ≤ u_{n} ≤ b$ et si ($u_{n}$) est une suite convergente, alors sa limte
appartient à l’intervalle [a , b].
P.7 : Limite et monotonie (Propriété fondamentale)
a) Toute suite croissante et majorée est convergente.
b) Toute suite décroissante et minorée est convergente.
Exemple : Soit ($u_{n}$) la suite définie par : $u_{n}=1+\frac{1}{1!}+\frac{1}{2!}+….+\frac{1}{n!}$ .
(Sur la notation n! , voir plus bas le cours de dénombrement. Notons simplement que par
définition : n ! = 1x2…xn.)
On a : $u_{n+1} = 1 +\frac{1}{1!}+\frac{1}{2!}+….+\frac{1}{n!}+\frac{1}{(n+1)!}=u_{n}+\frac{1}{(n+1)!}$ , donc $u_{n+1}─u_{n}={1}{(n+1)!}>0$
et par conséquent, la suite ($u_{n}$) est croissante (et même strictement croissante !).
Montrons que la suite ($u_{n}$) est majorée. Pour k ≥ 2, k ! = 2 × 3 × …. × k est le produit de (k ─
1) termes tous supérieurs ou égaux à 2, donc $k! ≥ 2^{k─1}$, si k ≥ 2, et $\frac{1}{k!}≤\frac{1}{2^{k─1}}$ . En ajoutant
membre à membre ces inégalités pour k allant de 2 à n, n ≥ 2, on obtient :
$\frac{1}{2!}+ ….+\frac{1}{n!}≤\frac{1}{2^{1}}+\frac{1}{2^{2}}+….+\frac{1}{2n─1}$ . Ajoutons 2 aux deux membres de cette égalité, en
remarquant que $1!=1$. On a : $u_{n} ≤ 1 + 1 +\frac{1}{2^{1}}+\frac{1}{2^{2}}+….+\frac{1}{2^{n─1}}$ .
Or, $1+\frac{1}{2}+(\frac{1}{2})^{2}+...+(\frac{1}{2})^{n-1}=\frac{1-(\frac{1}{2})^{n-1}}{1-\frac{1}{2}}=2(1-\frac{1}{2^{n}})$ et $1─\frac{1}{2^{n}}<1$.
Donc, pour tout entier naturel n, on a : $u_{n} ≤ 3$.
La suite ($u_{n}$) est croissante et majorée par 3 : elle admet donc une limite l ≤ 3. Cette limite
n’est autre que le célèbre nombre e, base des logarithmes népériens.
P.8 : Opérations sur les suites convergentes
Soient ($u_{n}$) et ($v_{n}$) deux suites de limites respectives l et k et soit λ un réel. Alors
a) La suite ($u_{n} + v_{n}$) converge vers le réel l + k.
b) La suite ($λ u_{n}$) converge vers le réel $\lambda{l}$.
c) La suite ($u_{n} u_{n}$) converge vers le réel l k.
d) Si k est non nul et si à partir d’un certain rang on a $v_{n} ≠ 0$, alors les suite $\frac{1}{v_{n}}$
et $\frac{u_{n}}{v_{n}}$
convergent respectivement vers les réels $\frac{1}{k}$ et $\frac{l}{k}$ .
7.4.1 Définition :
1°) On dit que la suite ($u_{n}$) tend vers (ou a pour limite $+\infty$) si et seulement si :
Pour tout réel A strictement positif, il existe un rang N tel que pour tout indice n, on ait :
$n\geq{N}u_{n} > A$.
On note alors $\lim\limits_{n\to +\infty}u_{n}=-\infty$.
2°) On dit que la suite ($u_{n}$) tend vers (ou a pour limite $-\infty$) si et seulement si :
Pour tout réel A strictement positif, il existe un rang N tel que pour tout indice n, on ait :
$n\geq{N}u_{n}< - A$.
On note alors $\lim\limits_{n\to +\infty}u_{n}=-\infty$.
2°) On dit que la suite ($u_{n}$) tend vers (ou a pour limite $-\infty$) si et seulement si :
Pour tout réel A strictement positif, il existe un rang N tel que pour tout indice n, on ait :
$n\in{N}\Rightarrow{ u_{n}< - A}$.
On note alors $\lim\limits_{n\to +\infty}u_{n}=-\infty$.
7.4.2 Exemple
Soit ($u_{n}$) la suite définie par $u_{n} = n$ . Montrons, en utilisant la définition précédente, que :$\lim\limits_{n\to +\infty}u_{n}=+\infty$. Soit A un réel strictement positif. Cherchons s’il existe un rang N tel que :
$n > N \Rightarrow{u_{n}> A}$. Or $u_{n} >A$ signifie que n > A, soit $n> A^{2}$. Il suffit donc de prendre $u_{n}$
entier N strictement supérieur à $A^{2}$. Prenons par exemple $N = E(a^{2}) + 1$.
Alors $n > N\Rightarrow{u_{n}}>A$.
7.4.3 Remarque
Soit ($u_{n}$) une suite du type $u_{n}= f(n)$ : Si $\lim\limits_{n\to +\infty}f(x)=+\infty$, alors $\lim\limits_{n\to +\infty}v_{n}=+\infty$. (Nous
admettrons ce résultat). Les théorèmes vus en Première sur les limites infinies de fonctions
s'appliquent donc aux suites de ce type. En conséquence, on récupère aussi dans ce cas tous
les théorèmes sur les opérations algébriques, les limites de référence, ainsi que les théorèmes
de comparaison.
7.4.4 Propriété (Comparaison)
1°) Soit ($u_{n}$) et ($v_{n}$) deux suites telles que :$\lim\limits_{n\to +\infty}v_{n}=+\infty$ et qu’à partir d’un certain rang, on
ait : $u_{n}\geq{v_{n}}$. Alors $\lim\limits_{n\to +\infty}u_{n}=-\infty$.
2°) Soit ($u_{n}$) et ($v_{n}$) deux suites telles que :$\lim\limits_{n\to +\infty}v_{n}=-\infty$ et qu’à partir d’un certain rang, on
ait : $u_{n} = v_{n}$. Alors $\lim\limits_{n\to +\infty}=u_{n}=+\infty$.
Exemple 1 : Soit ($u_{n})n\in\mathbb{N}$* la suite définie par : $u_{n} =\sum_{n}^{k=1}\frac{1}{\sqrt{p}}=1+\frac{1}{\sqrt{2}}+...+\frac{1}{\sqrt{n}}$
Si $1\geq{p}\geq{n}:1\geq{\sqrt{p}}\geq{\sqrt{n}}\Rightarrow\frac{1}{\sqrt{n}}\geq{\frac{1}{\sqrt{p}}}\geq{1}$. En sommant ces inégalités membre à
membre pour p allant de 1 à n, on obtient :$\frac{n}{\sqrt{n}}\geq{u_{n}}\geq{n}$. D’où :$\forall n\in \mathbb{N}*$, $u_{n}\geq{n}$.
On a :$\lim\limits_{n\to +\infty} \sqrt{n}=+\infty$ ,donc $\lim\limits_{n\to +\infty}u_{n} =+\infty$.
Exemple 2 :
Étudier la limite de la suite ($u_{n}$) définie, pour tout $n\in\mathbb{N}$, par :
$u_{n}=2\cos{n+3}\times{(-1)^{n}}-3n$.
On remarque que pour tout $n\in\mathbb{N}:u_{n}\geq{5-3n}$. (Encadrer cos n et remarquer que $(-1)^{n}\geq{1})$.
Or,$\lim\limits_{n\to +\infty}=(5-8n)=-\infty$ , d'où :$\lim\limits_{n\to +\infty}u_{n}=-\infty$.
Remarque : l'affirmation "une suite qui diverge vers $+\infty$ est nécessairement croissante" estelle
vraie ?
Réponse : non ! Considérer :$u_{n}=(-1)^{n}+n$. On a, pour tout $n\in\mathbb{N}:u_{n}=-1+n$.
Donc, par comparaison : ($u_{n}$) diverge vers $+\infty$ Cependant ($u_{n}$) n'est pas croissante. En effet,
pour tout $n\in\mathbb{N}$, on a :$u_{n+1}-u_{n} = (-1)^{n+1}(n+1)-(-1)^{n}-n =2\times{(-1)^{n+1}}+1$
D’où : $u_{n+1}-u_{n} = \left\{
\begin{array}{rl}
-1 si n est pair \\
3 si n est impair
\end{array}
\right.$
Donc la suite ($u_{n}$) n'est ni croissante, ni décroissante.
7.4.5 Extension des opérations
Nous admettrons les résultats suivants, regroupés sous forme de tableaux :
| $lim u_{n}$ | $lim v_{n}$ | $lim(u_{n}+v_{n})$ |
| $l$ | $+\infty$ | $+\infty$ |
| $l$ | $-\infty$ | $-\infty$ |
| $+\infty$ | $+\infty$ | $+\infty$ |
| $-\infty$ | $-\infty$ | $-\infty$ |
| $+\infty$ | $-\infty$ | Forme indéterminée |
| $lim \mid{u_{n}}\mid$ | $lim \mid{u_{n}}\mid$ | $lim\mid{u_{n}}v_{n}\mid$ | $lim\mid\frac{1}{u_{n}}\mid$ | $lim\mid\frac{1}{v_{n}}\mid$ |
| $l\ne{0}$ | $+\infty$ | $+\infty$ | 0 | 0 |
| O | $+\infty$ | Forme indéterminée | 0 | 0 |
| $+\infty$ | $+\infty$ | $+\infty$ | 0 | Forme indéterminée |
| $+\infty$ | $l\ne{0}$ | $+\infty$ | $\frac{1}{l}$ | $+\infty$ |
| $+\infty$ | 0 | $+\infty$ | $+\infty$ |
Remarques :
. Dans le dernier tableau, on suppose que les suites $(\frac{1}{u_{n}})$ et $(\frac{u_{n}}{v_{n}})$
sont définies, autrement dit,
qu’à partir d’un certain rang, tous les termes de la suite (vn) sont non nuls.
. Nous avons mis des valeurs absolues pour simplifier les tableaux. Dans les exercices, il
faudra déterminer le signe de $(u_{n}v_{n})$, $\frac{1}{u_{n}}$ et $\frac{u_{n}}{v_{n}}$
pour conclure.
. L’expression « forme indéterminée »signifie que l’on ne peut pas conclure directement dans
ce cas. Il faudra transformer l’expression de la suite d’une autre manière pour déterminer la
limite, si elle existe.
7.5 Convergence des suites arithmétiques et géométriques
7.5.1 Cas des suites arithmétiques
Une suite arithmétique diverge vers $+\infty$ si sa raison r est strictement positive et vers $-\infty$ si
sa raison r est strictement négative.
C’est une conséquence immédiate de la formule $u_{n} =u_{n} + (n ─ p)r$. Si p est fixé up est une
constante, tandis que (n ─ p)r tend vers $+\infty$ ou $-\infty$ suivant le signe de r.
7.5.2 Cas des suites géométriques
Soit ($u_{n}$) une suite définie par : $u_{n}=q_{n}$ (avec $q\in\mathbb{R}$)
.Si $q\in]1;+\infty[$ alors ($u_{n}$) est divergente (vers $+\infty$)
.Si q=1 alors ($u_{n}$) est constante (donc convergente vers 1)
.Si q=]-1;1[ alors ($u_{n}$) est convergente vers 0
.Si $q\in]-\infty;-1]$ alors ($u_{n}$) n'a pas de limite.
Démonstration :
Nous allons utiliser le résultat suivant :
Lemme Inégalité de Bernoulli
Pour tout réel x positif et tout entier naturel n, on $a:(1+x)^{n}≥ 1+nx$.
Démonstration du lemme :
Soit $x\in{R+}$. On considère la propriété p(n) définie pour tout $n\in\mathbb{ℕ}$ par :
$p(n):(1+x)^{n}≥ 1+nx$.
.On a p(0) puisque $(1+x)^{0}≥ 1+0x$ pour tout $x\in{R+}$.
.Montrons que, pour tout $n\in\mathbb{ℕ}:p(n)\Rightarrow{(n +1)}$.
Soit $n\in{\mathbb{ℕ}}$. Supposons $p(n):(1+x)^{n}≥ 1+nx$. Comme x>0, on a aussi 1+x>0. En
Soit $n\in\mathbb{ℕ}$. Supposons $p(n):(1+x)^{n}≥ 1+nx$. Comme x > 0, on a aussi 1+x>0. En
multipliant l'inégalité ci-dessus par (1+x), on obtient :$(1+x)^{n}(1+x) ≥(1+nx)(1+x)$.
Or : $(1+nx)(1+x)=1+x+nx+nx^{2}1+(n+1)x+nx^{2}$. Comme $nx^{2}≥0$, on a :
(1+nx)(1+x)≥ 1+(n+1)x. D'où:$(1+x)^{n}(1+x)≥ 1+(n+1)x$
Ce qui est p(n+1).
Bilan : on a p(0) et pour tout n de $\mathbb{ℕ}:p(n)\Rightarrow{p(n +1)}$
Donc, pour tout n de ℕ, on a : $p(n):(1+x)^{n}≥1+nx$.
Prouvons maintenant le théorème 7.5.2:
.Supposons $q\in]1;+\infty[$ . Posons x=q+1. Alors $x\in]0;+\infty[$ .
D'après l'inégalité de Bernoulli : $q_{n}=(1+x)^{n}≥1+nx$. Or,$\lim\limits_{n\to +\infty}1+nx=+\infty$. Par
comparaison, on en déduit :$\lim\limits_{n\to +\infty}q^{n}=+\infty$.
La suite ($u_{n}$) diverge donc vers $+\infty$.
.Si q=1, le résultat est évident.
.Supposons maintenant $q\in]-1 ; 1[$.
Si q=0, le résultat est évident.
Si $q\ne{0}$, posons : $q'=\frac{1}{|q|}$ . Ainsi :$q\in]1;+\infty[$. D'après le résultat précédent :
$\lim\limits_{n\to +\infty} a'^{n}=+\infty$ Par passage à l'inverse (cf. le deuxième tableau de 7.4.5), nous obtenons :
$\lim\limits_{n\to +\infty} |q|^{n}=0$. D'où :$\lim\limits_{n\to +\infty} q^{n}=0$. La suite ($u_{n}$) converge donc vers 0.
.Supposons q < ─ 1. Alors |q| > 1 et $\lim\limits_{n\to +\infty} |q|^{n}=+\infty$ d’après le 1er cas. Comme $q^{n}$ ne garde
pas un signe constant,$\lim\limits_{n\to +\infty} q^{n}$ n’existe pas.
7.6 Image d’une suite par une fonction
Nous admettrons le résultat suivant :
Théorème :
Soit ($u_{n}$) une suite telle que $\lim\limits_{n\to +\infty} u_{n}=\alpha$. Soit f une fonction telle que $\lim\limits_{n\to +\infty}f(x) = β$ et ($v_{n}$) la
suite définie par $v_{n} = f(u_{n})$. Alors $\lim\limits_{n\to +\infty} v_{n}=\beta$.
N.B.
.La suite ($v_{n}$) est appelée image (ou composée) de la suite ($u_{n}$) par la fonction f. Dans cet énoncé α et β peuvent être aussi bien des réels que $+\infty$ ou $+\infty$.
En particulier, si α est un réel et si f est continue au point α, alors β = f(α). D’où :
Corollaires :
1°) Soit ($u_{n}$) une suite convergeant vers un réel l et f une fonction continue au point l. Alors la
suite ($f(u_{n})$) converge vers f(l).
2°) Soit ($u_{n}$) une suite définie par une relation de récurrence de la forme $u_{n+1}=f(u_{n})$. Si ($u_{n}$)
converge vers l, et si f est une fonction continue au point l, alors on a nécessairement l’égalité
l = f(l).
N.B Le corollaire 2° est souvent utilisé dans la pratique.
Exemples :
1°) Soit ($v_{n}$) la suite définie par : $v_{n} =\frac{─ 2(0,3)^{n}+5}{(0,3)^{n}+1}$ .
Posons $u_{n} = (0,3)^{n}$. On a $v_{n} =f(u_{n})$ avec $f : x\rightarrow{─2x+5}$
x + 1 .$\lim\limits_{n\to +\infty}(0,3)^{n} = 0$(cf. paragraphe
précédent) et $\lim\limits_{x\to +\infty}f(x)=5$. Donc $\lim\limits_{n\to +\infty} v_{n} = 5$.
2°) Soit ($u_{n}$) la suite définie par la donnée de $u_{0} = 1$ et par la relation de récurrence, pour tout
entier naturel non nul n, $u_{n+1} =\sqrt{6+u_{n}}$ .
.Montrons d’abord par récurrence la propriété $p(n) :\forall n\in \mathbb{N}, 0 ≤ u_{n}≤ 3$. p(0) est vraie
par hypothèse et supposant p(n) vraie, on a (en ajoutant 6 aux trois membres de la double
inégalité) : $6 ≤ u_{n} + 6 ≤ 9\Rightarrow {\sqrt{6}}≤\sqrt{6+u_{n}} ≤ 3$, soit $6 ≤ u_{n+1} ≤ 3$, d’où p(n + 1) est vraie.
Il en résulte que p(n) est vraie pour tout entier naturel n.
.Montrons que la suite ($u_{n}$) est croissante. Pour tout entier naturel n, on a :
$u_{n+1} ─u_{n}=\sqrt{6 +u_{n}}─u_{n}=\frac{6+u_{n}─u_{n}^{2}}{6+u_{n}+u_{n}}$
(multiplication par l’expression conjuguée).
Soit $u_{n+1} ─u_{n} =\frac{─(u_{n}+2)(u_{n}─3)}{\sqrt{6+u_{n}}+u_{n}}$. D’après le point précédent, on voit que $u_{n+1}─u_{n}≥0$,
pour tout n(car $u_{n}+2 ≥ 0, u_{n}─3 ≤ 0,\sqrt{ 6+u_{n}}+u_{n}≥ 0$) , d’où le résultat.
;La suite ($u_{n}$) étant croissante et majorée par 3 converge d’après la propriété 7 du paragraphe
7.3. Soit l sa limite. D’après la propriété P.5 et le corollaire 2° ci-dessus, on doit avoir l ≥ 0 et
l = f(l), où f est la fonction $f : x \rightarrow{6 +x}$ (car f est continue sur [0; + ∞[, donc en particulier
au point l). L’équation $l = \sqrt{6+l}$ , avec l ≥ 0, équivaut à $l^{2}=6+l$ et a pour unique solution
positive l = 3. On en conclut que la suite ($u_{n}$) converge vers 3.
Exercices :
1) Montrer que la suite (($u_{n}$) telle que $u_{n}=\frac{\cos{(3n+1)}}{\sqrt{n}}$
converge vers 0.
2) Etudier la convergence des suites suivantes, de terme général un :
a) $u_{n} ={3n^{2}+(─1)^{n}n+4}{n{4}+1}$ b)$u_{n}= n^{2}(\sqrt{4+{1}{n^{2}}}─2)$ c)($u_{n}={n+1}{\sqrt{n+2}}─\frac{n+1}{n+3}$
d)($u_{n}=\frac{2n─\sqrt{4n^{2}─n+1}}{3n─\sqrt{9n{2}+n}}$ e)$u_{n}= \sqrt{9n^{4}+6n+2}─(3n^{2}+1)$ f)$u_{n}={4^{n}─3_{n+1}}{4^{n}+5}$
g) $u_{n}=\frac{3n+\sin{n}}{5n+2\cos{3n}}$ h)$u_{n}=\frac{1─\cos{\frac{1}{n}}}{n\sin{\frac{1}{n}}}$ i)$u_{n}=n(2+\cos{n^{2}}$).
3) Soit ($u_{n})n\in\mathbb{N}$ la suite réelle définie par son premier terme $u_{0}$ et par la condition :
pour tout n de $\mathbb{N}, u_{n+1} =u_{n}^{2} +u_{n}$.
a) Démontrer que la suite ($u_{n})n\in\mathbb{N}$ est croissante.
b) Démontrer que si ($u_{n}) n\in\mathbb{N}$ converge, alors $\lim\limits_{n\to +\infty} u_{n} =0$.
c) Démontrer que si $u_{0}+u_{0}^{2}>0$, alors la suite ($u_{n})n\in\mathbb{N}$ diverge.
d) Démontrer par récurrence que si $u_{0}+ u_{0}^{2} < 0$, alors pour tout n de $\mathbb{N}$, on a : $─ 1<u_{n}<0$.
Conclure alors sur la convergence de la suite ($u_{n})n\in\mathbb{N}$ .
4) Suites récurrentes linéaires
Soient a et b deux réels et ($u_{n})n\in\mathbb{N}$ la suite définie parla donnée de $u_{0}$ et de la relation de récurrence:
$u_{n+1}=au_{n}+b$.
A.a) Que peut-on dire de la suite ($u_{n}$) dans le cas où a = 1? Exprimer alors $u_{n}$ en fonction de $u_{0}$ et b et donner la
limite de la suite quand n tend vers $+\infty$.
b) Mêmes questions qu’au a) dans le cas où b = 0.
B. On suppose que $a\ne{1}$ et $b\ne{0}$.
a) Tracer les droites d’équations respectives y = ax + b et y = x dans un même repère orthonormé, puis
construire géométriquement les premiers termes de la suite en prenant $u_{0}=1$ dans chacun des cas suivants :
(a, b) = (2,─ 3) ; $(a,b)=(─\frac{1}{2},3$);(a,b) =(─1,3) .
b) Montrer que si la suite ($u_{n}$) converge, sa limite l vérifie $l=\frac{b}{1─a}$ .
c) Soit ($v_{n}$) la suite définie sur $\mathbb{N}$ par $v_{n}=u_{n}─l$. Montrer que la suite ($v_{n}$) est une suite géométrique dont on
précisera la raison.
d) Calculer $u_{0}$ en fonction de $u_{0}$, a, b et n.
e) Popur quelle valeur de u0 la suite ($u_{n}$) est-elle stationnaire?
f) Montrer que si |a| < 1, la suite ($u_{n}$) converge vers l.
g) Montrer que si a = ─ 1, la suite ($u_{n}$) est périodique.
h) Montrer que si la suite ($u_{n}$) n’est passtationnaire et si l’on a |a| > 1, alors les suites ($u_{n}$) et ($v_{n}$) sont
divergentes.
5) Suites récurrentes homographiques
A. On considère la suite ($u_{n}$) définie par:$u_{0}=1$ et $u_{n+1}=\frac{2+u_{n}}{u_{n}}$.
a) Quelles sont les limites éventuelles de cette suite ?
b) On pose $v_{n}=\frac{u_{n}─2}{u_{n}+1} (n\in\mathbb{N}$). Montrer que ($v_{n}$) est une suite géométrique de raison $─\frac{1}{2}$, puis exprimer $v_{n}$
en fonction

Ajouter un commentaire