Vous êtes ici

Bac Physique chimie 1er groupe S2, S2A, S4, S5 2024

Exercice 1

L'acétate de benzyle ou l'éthanoate de benzyle de formule chimique

$C_{9}H_{10}O_{2}$ est un composé important dans l'industrie des parfums et des arômes.

Apprécié pour son parfum floral et ses propriétés polyvalentes, il est utilisé comme solvant dans certaines synthèses organiques et il permet de donner le gout de fruits à des composés.

Au laboratoire, l'éthanoate de benzyle peut être synthétisé en faisant réagir le phénylméthanol de formule

$C_{6}H_{5}-CH_{2}-OH$ avec un acide carboxylique ou un de ses dérivés.

1.1 Synthèse de l'éthanoate de benzyle à partir de l'acide éthanoïque.

On mélange dans un ballon de l'acide éthanoïque et du phénylméthanol en présence d'acide sulfurique concentré.

On chauffe le mélange obtenu pendant quelques minutes.

1.1.1 Donner les caractéristiques de cette réaction.

Pourquoi ajoute-t-on de l'acide sulfurique ?

1.1.3 Écrire l'équation bilan de cette réaction.

1.2 Synthèse de l'éthanoate de benzyle à partir de l'anhydride éthanoïque.

On introduit dans un ballon du phénylméthanol de masse

$m_{1}=3.0\,g$ et de l'anhydride éthanoïque de volume

$V=2.50\,cm^{3}$ et quelques grains de pierre ponce puis on chauffe à reflux le mélange réactionnel pendant quelques minutes.

Après extraction et purification on obtient de l'éthanoate de benzyle de masse

$m_{2}=3.5\,g$

1.2.1 Quel est l'avantage de cette synthèse comparée à celle de la partie 1.1. ?

1.2.2 Écrire l'équation bilan de cette réaction.

1.2.3 Montrer qu'un réactif est utilisé en excès. Préciser lequel.

1.2.4 Calculer le rendement de cette réaction.

Masses molaires en

$g\cdot\,mol^{-1}$ : Anhydride éthanoïque :

$102$ ; éthanoate de benzyle :

$150$ ; Phénylméthanol :

$108$ ;

Masse volumique de l'anhydride éthanoïque en

$g\cdot\,cm^{-3}$ :

$1.08.$

1.3 Étude cinétique de la synthèse de l'éthanoate de benzyle à partir de l'anhydride.

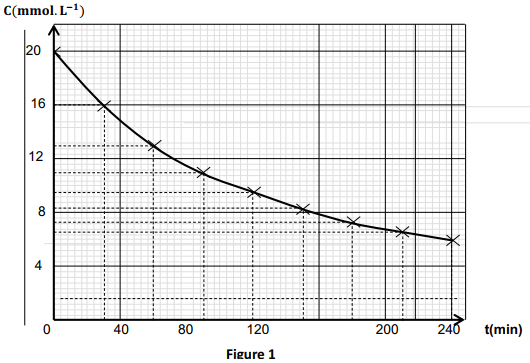
Le suivi par titrage a permis d'obtenir le tracé de l'évolution de la concentration C en anhydride éthanoïque en fonction du temps

$t.$ (Figure 1).

1.3.1 Déterminer les vitesses volumiques de disparition de cette réaction aux dates

$t_{1}=40\,min\text{ et }t_{2}=120\,min$

1.3.2 Définir et déterminer le temps de demi-réaction.

Exercice 2

Les amines sont des composés organiques qui peuvent être considérés comme des dérivés de l'ammoniac

$\left(NH_{3}\right)$ où un ou plusieurs des atomes d'hydrogène sont remplacés par des groupes alkyle ou aryle.

Elles jouent un rôle crucial dans divers domaines, notamment la chimie, la biologie, et l'industrie.

Ayant des propriétés basiques, les amines sont utilisées pour la synthèse de médicaments, de colorants et de fibres textiles.

Un groupe d'élèves se propose d'étudier une amine notée

$B.$

Pour cela, les élèves introduisent une solution aqueuse de l'amine

$B$ de concentration molaire

$C_{0}$ inconnue et de volume

$V_{0}=20\,mL$ dans une fiole jaugée de

$500\,mL.$

Ils complètent jusqu'au trait de jauge avec de l'eau distillée.

Ils obtiennent ainsi une solution aqueuse

$S.$

Les élèves dosent un volume

$V=20\,mL$ de la solution

$S$ à l'aide d'une solution d'acide chlorhydrique

$\left(H_{3}O^{+}+Cl^{-}\right)$ de concentration molaire

$C_{a}=0.05\,mol\cdot L^{-1}.$

Le dosage suivi au

$pH-$ mètre a permis d'obtenir le tableau de valeurs suivant à

$25^{\circ}C$ :

$\begin{array}{|l|c|c|c|c|c|c|c|c|c|c|c|c|c|c|} \hline V_{a}(mL)&10&15&20&25&30&35&36&38&39&40&41.5&43&45&50\\ \hline pH&11.1&10.9&10.7&10.5&10.2&9.8&9.7&9.3&8.5&6.1&3.3&2.7&2.4&2.1\\ \hline \end{array}$

2.1 Définir une base selon Bronsted.

2.2 Faire un schéma annoté du dispositif de dosage.

2.3 Afin de déterminer les caractéristiques de l'amine, les élèves exploitent la courbe de variation

$pH=f\left(V_{a}\right)$

2.3.1 Tracer la courbe de variation du

$pH$ du milieu en fonction du volume

$V_{a}$ d'acide versé.

Échelles :

$1\,cm$ pour

$5\,mL$ et

$1\,cm$ pour une unité de

$pH$

2.3.2 Déterminer graphiquement les coordonnées du point d'équivalence et la valeur du

$pKa$ du couple acide/base.

En déduire la formule et le nom de la base dosée.

On donne :

$\left(CH_{3}\right)_{3}NH^{+}/\left(CH_{3}\right)_{3}N\ :\ pKa=9.8$ ;

$C_{2}H_{5}NH_{3}^{+}/C_{2}H_{5}NH_{2}\ :\ pKa=10.7$

$NH_{4}^{+}/NH_{3}\ :\ pKa=9.2.$

2.3.3 Déterminer la concentration

$C_{0}$ de la solution de base.

2.3.4 Calculer les concentrations des espèces chimiques

$B$ de la base et

$BH^{+}$ de son acide conjugué en solution au moment où le volume d'acide chlorhydrique versé vaut

$40\,mL.$

Retrouver la valeur du

$pKa$ du couple

$BH^{+}/B.$

2.4 L'acide chlorhydrique réagit avec l'amine notée

$B$ dont l'acide conjugué est noté

$BH^{+}.$

2.4.1 Écrire l'équation bilan de la réaction support du dosage.

2.4.2 Calculer la constante de réaction

$Kr.$ Conclure.

2.5 En fait, l'amine est le produit d'une réaction de décarboxylation d'un acide

$\alpha-$ aminé noté

$R-CH\left(NH_{2}\right)COOH.$

Écrire l'équation de décarboxylation et identifier

$R$

Exercice 3

Le spectrographe de masse est une technique analytique essentielle et polyvalente avec des applications vastes et diversifiées.

Son importance réside dans sa capacité à fournir des informations précises et détaillées sur la masse et la structure des composés chimiques, ce qui est crucial pour la recherche scientifique, le diagnostic médical, l'analyse environnementale, la sécurité alimentaire, et bien d'autres domaines.

On considère un dispositif d'analyse de particules, constitué de trois parties : une chambre d'accélération, un filtre de vitesse et une chambre de déviation. (Figure 2)

3.1 Accélération des ions

Des ions positifs isotopes du cuivre

$^{63}Cu^{2+}\text{ et }^{x}Cu^{2+}$ de même charge

$q=2e$ , de masse respective

$m=63u$ et

$m'=xu$ , émis à partir du point

$O_{1}$ avec une vitesse initiale négligeable, sont accélérés entre

$O_{1}$ et

$O_{2}$ par la tension

$U_{0}$ existant entre les plaques

$P_{1}$ et

$P_{2}$ telle que

$\left|U_{0}\right|=\left|U_{P_{1}}-{P}_{2}\right|=5\cdot 10^{3}V.$

Ils se déplacent dans le vide suivant la direction horizontale de

$O_{1}$ vers

$O_{2}.$

On négligera le poids des ions devant les autres forces.

On donne :

$e=1.6\cdot 10^{-19}C$ et

$u=1.67\cdot 10^{-27}kg$

3.1.1 Quel est le signe de la tension

$U_{P_{1}P_{2}}$ ?Justifier.

3.1.2 Calculer la vitesse

$v$ de l'isotope

$^{63}Cu^{2+}$ en

$O_{2}.$

3.1.3

$v$ et

$v'$ désignent respectivement les vitesses en

$O_{2}$ des deux isotopes

$^{63}Cu^{2+}\text{ et }^{x}Cu^{2+}$ .

Établir la relation entre

$v\;,\ v'\;,\ m\text{ et }m'.$

3.1.4 Le rapport

$\dfrac{v}{v'}=1.016$ ; en déduire la valeur entière

$x$ du nombre de masse de l'ion

$^{x}Cu^{2+}.$

3.2 Filtre de vitesse

Arrivés en

$O_{2}$ , les ions pénètrent dans un filtre de vitesse constitué par : deux plaques horizontales

$P$ et

$Q$ distantes de

$d=20\,cm$ entre lesquelles on établit une différence de potentiel

$U=V_{P}-V_{Q}=1.50\cdot 10^{3}V$ = créant un champ électrique

$\overrightarrow{E}.$

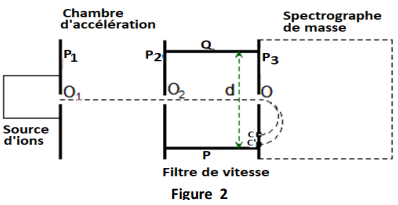
$\surd\$ un dispositif adéquat crée dans l'espace situé entre les deux plaques un champ magnétique

$\overrightarrow{B}$ perpendiculaire aux vitesses

$\overrightarrow{v}$ et

$\overrightarrow{v'}$ ainsi qu'au champ électrique

$\overrightarrow{E}.$

3.2.1. Déterminer le sens du champ magnétique

$\overrightarrow{B}$ pour que les ions

$^{63}Cu^{2+}$ , arrivant en

$O_{2}$ , traversent le dispositif par un mouvement rectiligne uniforme avec la vitesse

$v.$

3.2.2. Exprimer l'intensité

$B$ du champ magnétique en fonction de

$v\;,\ U\;,\ d.$ Calculer

$B.$

Dans quel sens sont alors déviés les ions

$^{x}Cu^{2+}$ ?

3.2.3 Déterminer la valeur

$B'$ du champ magnétique pour que les ions

$^{x}Cu^{2+}$ traversent le dispositif sans subir de déviation.

3.3 Spectrographe de masse

En faisant varier la valeur du champ magnétique

$B$ dans le filtre de vitesse, on peut faire passer par le point

$O$ l'un ou l'autre des isotopes. Les ions pénètrent alors dans la chambre de déviation où règne un champ magnétique

$\overrightarrow{B_{0}}$ d'intensité

$B_{0}=0.5\,T\cdot C$ et

$C'$ sont les points d'impact respectifs des ions

$^{63}Cu^{2+}$ et

$^{x}Cu^{2+}$ (fig 2)

3.3.1 Établir l'expression du rayon

$R$ de la trajectoire de l'ion

$^{63}Cu^{2+}.$ Calculer

$R.$

3.3.2 On place au niveau des collecteurs

$C$ et

$C'$ un dispositif permettant de mesurer les intensités des courants

$I$ et

$I'$ correspondant au nombre d'ions

$N$ et

$N'$ y arrivant par seconde.

On trouve que

$I=\dfrac{7}{3}I'.$

En déduire les pourcentages en ions

$^{63}Cu^{2+}\text{ et }^{x}Cu^{2+}$ dans le cuivre naturel.

Exercice 4

Une bobine s'oppose aux variations de l'intensité du courant.

Un condensateur filtre les fréquences de signaux pour la qualité de leur transmission dans un système électrique.

Ils sont généralement associés à une résistance pour former un circuit

$RLC$ qui peut produire, entre autres, un phénomène de résonance qu'on retrouve dans le fonctionnement des radios et télévisions.

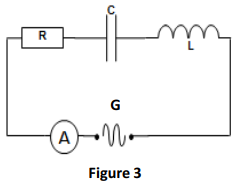
Au cours d'une séance de travaux pratiques, un technicien associe en série un générateur délivrant une tension alternative sinusoïdale de fréquence

$N$ , de valeur maximale

$U_{m}$ et d'expression

$u(t)=U_{m}\cos(2\pi Nt)$ , un résistor de résistance

$R=16\Omega$ , une bobine d'inductance

$L$ et de résistance négligeable, un condensateur de capacité

$C$ et un ampèremètre (figure 3).

Un oscilloscope bicourbe permet de visualiser les tensions

$u(t)$ aux bornes du générateur et

$u_{L}(t)$ aux bornes de la bobine lorsque le circuit est fermé (figure 4).

On donne

$u_{L}(t)=U_{Lm}\cos\left(2\pi Nt+\varphi_{uL/u}\right)$ où

$U_{Lm}$ est la tension maximale aux bornes de la bobine et

$\varphi_{uL/u}$ le déphasage de la tension aux bornes de la bobine

$u_{L}$ par rapport à celle du générateur

$u$

4.1 Reproduire la figure 3 sur la copie et préciser les branchements de l'oscilloscope permettant de visualiser

$u$ et

$uL.$

4.2 On considère les oscillogrammes représentés à la figure 4.

On donne la base de temps :

$2.5\,ms/div$ et sensibilité verticale :

$2V/div$

4.2.1 identifier

$uL(t)$ sachant que la tension

$uL(t)$ est en avance de phase sur

$u(t).$

4.2.2 Déterminer :

$-\$ les tensions maximales

$U_{m}$ aux bornes du générateur et

$U_{Lm}$ aux bornes de la bobine ;

$-\$ la fréquence

$N$ de la tension

$u(t)$ délivrée par le générateur ;

$-\$ la phase

$\left(\varphi_{uL/u}\right)$ de la tension

$u_{L}(t)$ par rapport à la tension

$u(t).$

4.3 l'expression de la tension aux bornes générateur est

$u(t)=U_{m}\cos\left(2\pi Nt+\varphi_{uL/u}\right)$ et celle aux bornes de la bobine est :

$u_{L}(t)=U_{Lm}\cos\left(2\pi Nt+\varphi_{uL/u}\right)$

4.3.1 Écrire les équations horaires numériques des tensions

$u(t)$ et

$u_{L}(t).$

4.3.2 Déterminer la phase

$\left(\varphi_{i/u}\right)$ de l'intensité

$i(t)$ du courant par rapport à la tension

$u(t)$ aux bornes du générateur sachant que

$\varphi_{i/u}=\varphi_{i/uL}+\varphi_{uL/u}.$

4.3.3 Justifier que le circuit est à la résonance d'intensité.

4.4 Déterminer :

$\surd\$ la valeur de l'intensité du courant mesurée par l'ampèremètre ;

$\surd\$ la valeur de l'inductance

$L$ ;

$\surd\$ la capacité

$C$ ;

$\surd\$ la largeur de la bande passante en fréquence

$\Delta N.$

Exercice 5

$1887$ le physicien allemand Heinrich HERTZ réalise des expériences sur les ondes électromagnétiques de grandes longueurs d'onde.

Il remarque alors qu'un rayonnement peut favoriser des décharges électriques.

Par ailleurs, l'analyse des spectres lumineux émis par un atome a permis d'expliquer la quantification de l'énergie de l'atome.

5.1 Étude de l'effet photoélectrique

Dans un laboratoire, on utilise un laser qui émet une lumière monochromatique de longueur d'onde

$\lambda=435.3\│,nm.$

On éclaire une plaque de métal avec cette radiation lumineuse.

Un capteur détecte un électron d'énergie cinétique

$E_{c}=0.55\,eV.$

5.1.1- Définir l'effet photoélectrique.

Quel modèle de la lumière permet de l'expliquer ?

5.1.2 Calculer la vitesse de l'électron émis.

5.1.3 Définir le travail d'extraction

$W_{0}$ puis calculer sa valeur pour le métal utilisé.

5.1.4 On éclaire le même métal par un autre laser de longueur d'onde

$\lambda_{1}=580\,nm.$

L'effet photo électrique est-il toujours observé ? Justifier la réponse.

5.2 Niveaux d'énergie de l'atome d'hydrogène

On rappelle que les niveaux d'énergie de l'atome d'hydrogène sont quantifiés et ont pour expression

$E_{n}=-\dfrac{E_{0}}{n^{2}}$ ;

$E_{0}=13.6\,eV$ ;

$n$ entier naturel non nul.

5.2.1 L'atome est au niveau d'énergie

$n=2.$

Il absorbe un photon de longueur d'onde

$\lambda=435.3\,nm.$

On note une transition du niveau d'énergie

$n=2$ au niveau d'énergie

$m.$

Déterminer la valeur de

$m$ puis schématiser la transition électronique correspondante.

5.2.2 On éclaire le tube rempli de gaz hydrogène se trouvant à l'état fondamental avec un photon d'énergie

$E=14.0\,eV.$

Quel est l'état final de l'atome d'hydrogène ?

Données : Constante de Planck ;

$h=6.63\cdot 10^{-34}J\cdot s$ ;

Électron volt

$(eV)\ :\ 1.6\cdot 10^{-19}J$ ;

célérité de la lumière :

$c=3.0\cdot 10^{8}m\cdot s^{-1}$ ;

masse électron

$m_{e}=9.1\cdot 10^{-31}kg$ ;

nanomètre :

$1\,nm=10^{-9}m.$

Commentaires

Anonyme (non vérifié)

jeu, 08/15/2024 - 18:19

Permalien

Merci on peut avoir le

Merci on peut avoir le corrigé

répondre

Ajouter un commentaire

form.antibot { display: none !important; } You must have JavaScript enabled to use this form.