Corrigé Exercice 7 : Théorème de Thalès - 3e

 

$ABCD$ est un carré.

 

$E$ est le point de $[AD]$ tel que $AE=\dfrac{1}{3}AD.$

 

$F$ est le point de $[AB]$ tel que $AF=\dfrac{1}{3}AB.$

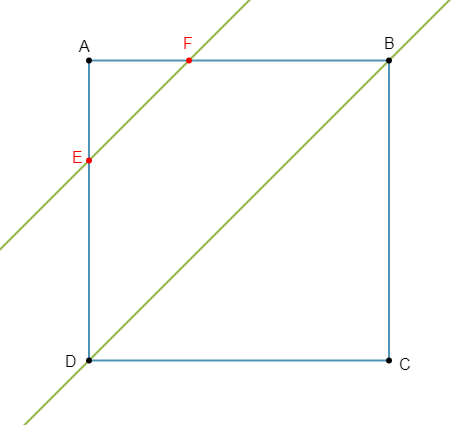
1) Démontrons que les droites $(EF)\ $ et $\ (BD)$ sont parallèles.

 

On a : $A\;,\ F\;,\ B$ sont trois points alignés d'une part, et $A\;,\ E\;,\ D$ sont trois points alignés d'autre part, dans le même ordre.

 

Calculons les rapports $\dfrac{AF}{AB}\quad\text{et}\quad\dfrac{AE}{AD}$

 

On a :

 

$AF=\dfrac{1}{3}AB\ \Rightarrow\ \dfrac{AF}{AB}=\dfrac{1}{3}$

 

$AE=\dfrac{1}{3}AD\ \Rightarrow\ \dfrac{AE}{AD}=\dfrac{1}{3}$

 

On constate alors que : $\dfrac{AF}{AB}=\dfrac{AE}{AD}$

 

Ainsi, d'après la réciproque du théorème de Thalès, les droites $(EF)\ $ et $\ (BD)$ sont parallèles.

 

2) a) Pour obtenir la longueur $EF$, on doit multiplier la longueur $BD$ par $\dfrac{1}{3}.$

 

Justifions la réponse.

 

En effet, les droites $(EF)\ $ et $\ (BD)$ étant parallèles alors, les triangles $AEF\ $ et $\ ABD$ sont en position de Thalès.

 

Donc, d'après le théorème de Thalès, les longueurs des côtés correspondants sont proportionnelles.

 

Par suite, le triangle $AEF$ est une réduction du triangle $ABD.$

 

Or, $\dfrac{AF}{AB}=\dfrac{AE}{AD}=\dfrac{1}{3}$ donc, le coefficient de réduction est égal à : $\dfrac{1}{3}.$

 

Par conséquent, $\boxed{EF=\dfrac{1}{3}\times BD}$

 

b) Pour obtenir l'aire de $AEF$, on doit multiplier l'aire du triangle $ABD$ par $\left(\dfrac{1}{3}\right)^{2}.$

 

Justifions

 

En effet, les triangles $AEF\ $ et $\ ABD$ étant en position de Thalès avec un coefficient de réduction de $\dfrac{1}{3}$ alors, le coefficient de réduction des aires est égal à $\left(\dfrac{1}{3}\right)^{2}.$ Soit : $\dfrac{1}{9}.$

 

D'où, $\boxed{\text{Aire}(AEF)=\dfrac{1}{9}\times \text{Aire}(ABD)}$