Corrigé Exercice 14 : Théorème de Thalès - 3e
Classe:
Troisième
Exercice 14
Soit $ABC$ un triangle tel que :
$$AB=10\,cm\;,\ AC=7.5\,cm\ \text{ et }\ BC=12.5\,cm$$
1) Montrons que $ABC$ est un triangle rectangle en $A.$
Pour cela, calculons les carrés des longueurs des côtés du triangle.
On a :
$BC^{2}=(12.5)^{2}=156.25$
$AB^{2}=10^{2}=100$
$AC^{2}=(7.5)^{2}=56.25$
Alors, $AB^{2}+AC^{2}=100+56.25=156.25$
On constate que : $AB^{2}+AC^{2}=BC^{2}$
Par conséquent, d'après la réciproque du théorème de Pythagore, le triangle $ABC$ est rectangle en $A.$
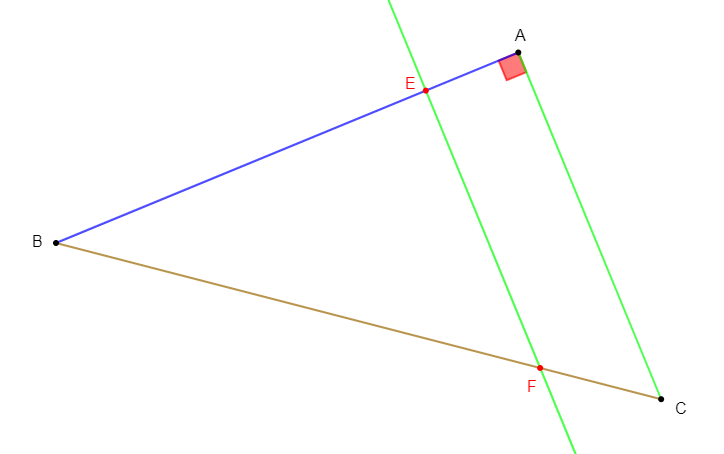
2) Soit $E$ le point du segment $[AB]$ tel que $AE=2\,cm.$
La perpendiculaire à $(AB)$ passant par $E$ coupe $(BC)$ au point $F.$
a) Montrons que $(AC)\ $ et $\ (EF)$ sont parallèles.
On a : $(AC)\ $ et $\ (EF)$ sont deux droites perpendiculaires à la droite $(AB).$
Or, on sait que deux droites sont perpendiculaires à une même droite sont parallèles.
Par conséquent, $(AC)\ $ et $\ (EF)$ sont parallèles.
b) Calculons les distances $BE\;,\ EF\ $ et $\ BF.$
$-\ $ Calcul de $BE$
Comme $E\in[AB]$ alors, $BE=AB-AE$
En remplaçant $AB\ $ et $\ AE$ par leur valeur, on trouve : $BE=10-2=8$
D'où, $\boxed{BE=8\;cm}$
$-\ $ Calcul de $EF$
Les droites $(AC)\ $ et $\ (EF)$ étant parallèles alors, les triangles $ABC\ $ et $\ AEF$ sont en position de Thalès.
Ainsi, d'après le théorème de Thalès, on a :
$$\dfrac{EF}{AC}=\dfrac{BE}{AB}$$
Alors, en remplaçant $AC\;,\ BE\ $ et $\ AB$ par leur valeur, on obtient :
$\begin{array}{rcl}\dfrac{EF}{7.5}=\dfrac{8}{10}&\Leftrightarrow&10\times EF=7.5\times 8\\\\&\Leftrightarrow&EF=\dfrac{60}{10}\\\\&\Leftrightarrow&EF=6\end{array}$
D'où, $\boxed{EF=6\;cm}$
$-\ $ Calcul de $BF$
En appliquant encore le théorème de Thalès, on a :
$$\dfrac{BF}{BC}=\dfrac{BE}{AB}$$
Donc, en remplaçant $BC\;,\ BE\ $ et $\ AB$ par leur valeur, on obtient :
$\begin{array}{rcl}\dfrac{BF}{12.5}=\dfrac{8}{10}&\Leftrightarrow&10\times BF=12.5\times 8\\\\&\Leftrightarrow&BF=\dfrac{100}{10}\\\\&\Leftrightarrow&BF=10\end{array}$
D'où, $\boxed{BF=10\;cm}$

Ajouter un commentaire