Corrigé Exercice 19 : Théorème de Thalès - 3e

 

Répondons par vrai ou faux :

 

1) $FEG$ est un triangle, $M\in[FE]\ $ et $\ N\in[FG]$ tels que : $(MN)\parallel (EG)$, d'après la réciproque du théorème de Thalès $\dfrac{FM}{FE}=\dfrac{FN}{FG}\quad\text{Faux}$

 

C'est le théorème de Thalès qui permet d'avoir cette égalité et non sa réciproque.

 

2) Si, $MAN$ est un triangle ; $M\;,\ I\;,\ A$ d'une part et $M\;,\ J\;,\ N$ d'autre part sont alignés dans le même ordre et $\dfrac{MI}{MA}=\dfrac{MN}{MJ}$ alors, $(IJ)\parallel (AN)\quad\text{Faux}$

 

C'est l'égalité $\dfrac{MI}{MA}=\dfrac{MJ}{MN}$ qui permet de conclure que $(IJ)\parallel (AN).$

 

3) Si, deux triangles sont en position de Thalès alors, les supports de deux de leurs côtés sont parallèles.$\quad\text{Vrai}$

 

4) $MNL\ $ et $\ MAB$ sont deux triangles tels que $(NL)\parallel (AB)$ alors, $MNL\ $ et $\ MAB$ sont en position de Thalès.$\quad\text{Faux}$

 

Pour cela, il faut ajouter la condition suivante : $N\in(MA)\ $ et $\ L\in(MB).$

 

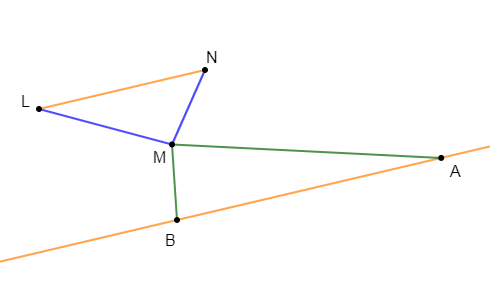
Exemple : Sur la figure ci-dessous, les droites $(NL)\ $ et $\ (AB)$ sont parallèles mais les deux triangles $MNL\ $ et $\ MAB$ ne sont pas en position de Thalès parce que les points $A\;,\ M\;,\ L$ d'une part et $B\;,\ M\;,\ N$ d'autre part, ne sont pas alignés.

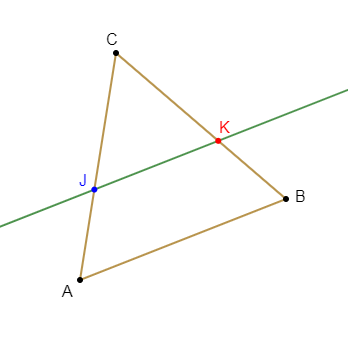
5) Si $ABC$ est un triangle, $K\in[BC]$ et la parallèle à $(AB)$ passant par $K$ coupe $(AC)$ en $J$ alors $CKJ\ $ et $\ CBA$ sont des triangles en position de Thalès.$\quad\text{Vrai}$