Corrigé Exercice 12 : Les lentilles minces 3e
Classe:
Troisième
Exercice 12 Construction de l'image d'un objet réel donnée par une lentille convergente
Un objet lumineux $AB$ de hauteur $2\;cm$ est placé perpendiculairement à l'axe optique principal d'une lentille convergente de centre optique $O$ et de distance focale $3\;cm.$
Le point $A$ est sur l'axe optique principal, à $6\;cm$ de $O$
1) Calculons la vergence de la lentille
Soit $C$ la vergence de cette lentille alors, on a : $$C=\dfrac{1}{f}$$
où $f$ est la distance focale
A.N : $C=\dfrac{1}{3\;10^{-2}}=33.3$
D'où, $\boxed{C=33.3\;\delta}$
2) Construisons l'image $A'B'$ de $AB$
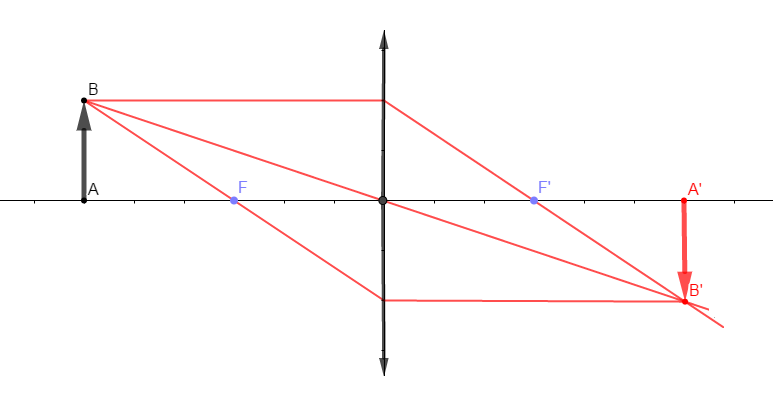
3) Donnons les caractéristiques de l'image $A'B'$
$-\ $ image réelle
$-\ $ image renversée
$-\ $ la taille de l'image est égale à celle de l'objet
$-\ $ image symétrique à l'objet par rapport au centre optique.
4) Déterminons le grandissement $G$ de l'image
Le grandissement $G$ de l'image est donné par : $$G=\dfrac{A'B'}{AB}$$
Comme l'image et l'objet ont la même taille alors, $\ AB=A'B'$
D'où, $$G=1$$
5) Reprenons les mêmes questions pour les cas suivants :
a) L'objet est placé à $7\;cm$ du centre optique
$\centerdot\ \ $ Vergence de la lentille
$$C=\dfrac{1}{f}$$
où $f$ est la distance focale
Ainsi, $C=\dfrac{1}{3\;10^{-2}}=33.3\;\delta$
$\centerdot\ \ $ Construction de l'image $A'B'$ de $AB$
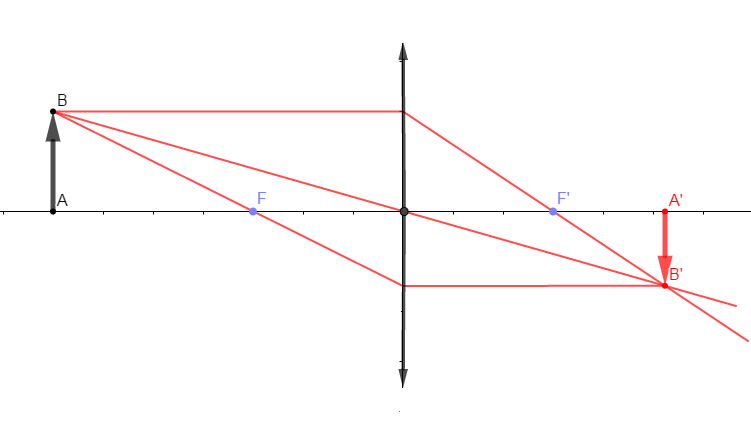
$\centerdot\ \ $ Caractéristiques de l'image $A'B'$ :
$-\ $ image réelle
$-\ $ image renversée
$-\ $ image plus petite que l'objet
$-\ $ image sur le côté opposé telle que $OA'=5.1\;cm$
$\centerdot\ \ $ Grandissement $G$ de l'image
On a : $G=\dfrac{A'B'}{AB}\ $ or, $\dfrac{A'B'}{AB}=\dfrac{OA'}{OA}$
Donc, $G=\dfrac{OA'}{OA}=\dfrac{5.1}{7}=0.7$
D'où, $$G=0.7$$
b) L'objet est placé à $5\;cm$ du centre optique
$\centerdot\ \ $ Vergence de la lentille
$$C=\dfrac{1}{f}$$
où $f$ est la distance focale
Donc, $C=\dfrac{1}{3\;10^{-2}}=33.3\;\delta$
$\centerdot\ \ $ Construction de l'image $A'B'$ de $AB$
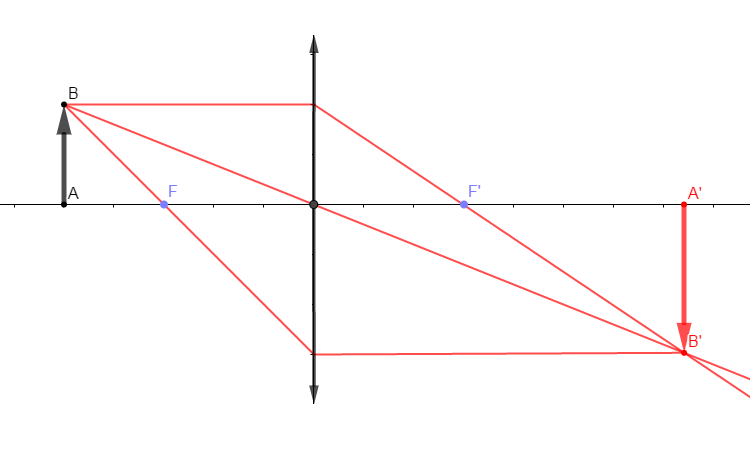
$\centerdot\ \ $ Caractéristiques de l'image $A'B'$ :
$-\ $ image réelle
$-\ $ image renversée
$-\ $ image plus grande que l'objet
$-\ $ image sur le côté opposé telle que $OA'=7.2\;cm$
$\centerdot\ \ $ Grandissement $G$ de l'image
On a : $G=\dfrac{A'B'}{AB}\ $ or, $\dfrac{A'B'}{AB}=\dfrac{OA'}{OA}$
Donc, $G=\dfrac{OA'}{OA}=\dfrac{7.2}{5}=1.4$
D'où, $$G=1.4$$
c) L'objet est placé sur le foyer objet
$\centerdot\ \ $ Vergence de la lentille
$$C=\dfrac{1}{f}$$
où $f$ est la distance focale
Ainsi, $C=\dfrac{1}{3\;10^{-2}}=33.3\;\delta$
L'objet étant placé sur le foyer $F$ alors, son image $A'B'$ est infinie.
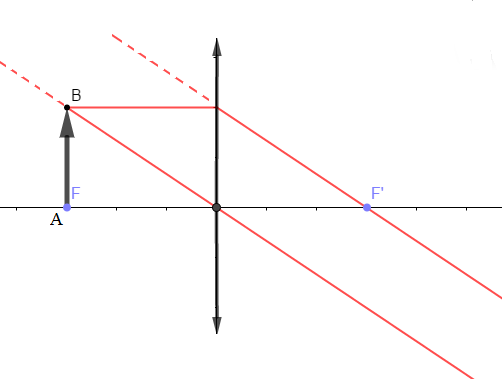
d) L'objet est placé à $2\;cm$ du centre optique
$\centerdot\ \ $ Vergence de la lentille
$$C=\dfrac{1}{f}$$
où $f$ est la distance focale
Donc, $C=\dfrac{1}{3\;10^{-2}}=33.3\;\delta$
$\centerdot\ \ $ Construction de l'image $A'B'$ de $AB$
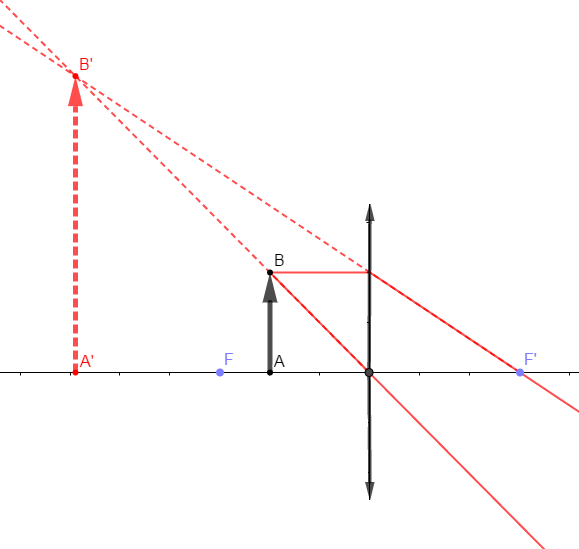
$\centerdot\ \ $ Caractéristiques de l'image $A'B'$ :
$-\ $ image virtuelle (non observable)
$-\ $ image droite (non renversée)
$-\ $ image plus grande que l'objet
$-\ $ image du même côté que l'objet telle que $OA'=5.9\;cm$
$\centerdot\ \ $ Grandissement $G$ de l'image
On a : $G=\dfrac{A'B'}{AB}=\dfrac{OA'}{OA}$
D'où, $G=\dfrac{5.9}{2}=2.9$

Ajouter un commentaire