Corrigé Exercice 4 : Distances - 4e

Classe:

Quatrième

1) Construisons un triangle quelconque

$ABC$ , et choisis un point

$R$ sur le segment

$[BC].$

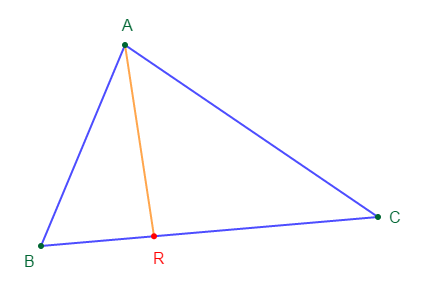
On note

$p$ le périmètre du triangle

$ABC.$

2) Démontrons que

$AR<\dfrac{p}{2}$

$-\$ En appliquant l'inégalité triangulaire sur le triangle

$ARB$ , on obtient :

$AR<AB+BR\qquad\text{(inégalité 1)}$

$-\$ En appliquant l'inégalité triangulaire sur le triangle

$ARC$ , on obtient :

$AR<AC+CR\qquad\text{(inégalité 2)}$

$-\$ En additionnant les inégalités (1) et (2) membre à membre, on trouve :

$AR+AR<AB+BR+AC+CR$

Ce qui est équivalent à :

$2AR<AB+BR+CR+AC\qquad\text{(inégalité 3)}$

Comme

$R\in[BC]$ alors,

$BR+CR=BC$

Par suite, en remplaçant

$BR+CR$ par

$BC$ dans l'inégalité (3), on obtient :

$2AR<AB+BC+AC\qquad\text{(inégalité 4)}$

Or,

$\ AB+BC+AC=p$ donc, en remplaçant

$AB+BC+AC$ par

$p$ dans l'inégalité (4), on obtient :

$2AR<p\ \Rightarrow\ AR<\dfrac{p}{2}$

Ainsi,

$\boxed{AR<\dfrac{p}{2}}$

Auteur:

Ajouter un commentaire

form.antibot { display: none !important; } You must have JavaScript enabled to use this form.