Corrigé Exercice 5 : Distances - 4e

 

Soient $A\ $ et $\ B$ deux points distincts du plan.

 

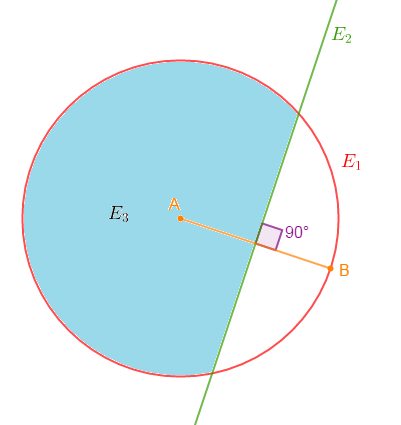
1) Construisons l'ensemble $E_{1}$ des points $M$ du plan tels que : $AM=AB.$

 

$AM=AB$ signifie que les points $M$ sont équidistants à un point fixe $A.$ De plus, leur distance par rapport à ce point $A$ est égale à $AB.$

 

Cela définit alors un cercle de centre $A$ et de rayon $AB.$

 

D'où, l'ensemble $E_{1}$ des points $M$ du plan tels que $AM=AB$ est le cercle de centre $A$ et passant par $B.$

 

2) Traçons l'ensemble $E_{2}$ des points $N$ du plan tels que : $AN=BN.$

 

Soit : $AN=BN$ alors, $N$ est équidistant des points $A\ $ et $\ B.$

 

Or, tous les points appartenant à la médiatrice de $[AB]$ sont équidistants des points $A\ $ et $\ B.$

 

Donc, l'ensemble $E_{2}$ des points $N$ du plan tels que $AN=BN$ est la médiatrice du segment $[AB].$ C'est la droite perpendiculaire à $(AB)$ et passant par le milieu de $[AB].$

 

3) Colorions en bleu l'ensemble $E_{3}$ des points $M$ du plan tels que : $AM<BM\ $ et $\ AM<AB.$

 

En effet :

 

$-\ $ l'ensemble $E_{2}$ divise le plan en deux parties ; la partie contenat le point $A$ et la partie contenant le point $B.$ Donc, les points $M$ tels que $AM<BM$ sont situés dans la partie contenat le point $A.$

 

$-\ $ l'ensemble $E_{1}$ divise le plan en deux parties ; la partie intérieure au cercle et la partie extérieure au cercle. Ainsi, les points $M$ du plan tels que $AM<AB$ sont les points qui se sont situés à l'intérieur du cercle.

 

D'où, l'ensemble $E_{3}$ des points $M$ du plan tels que $AM<BM\ $ et $\ AM<AB.$ sera constitué des points situés à la fois, à gauche de la médiatrice de $[AB]$ et à l'intérieur du cercle de centre $A$ passant par $B.$