Corrigé Exercice 8 : Distances - 4e

 

1) On donne $(D)$ et un point $B$ situé à $1\;cm$ de $(D).$

 

2) Construisons les droites $(D_{1})$ et $(D_{2})$ parallèle à $(D)$ et situées à $2\;cm$ du point $B.$

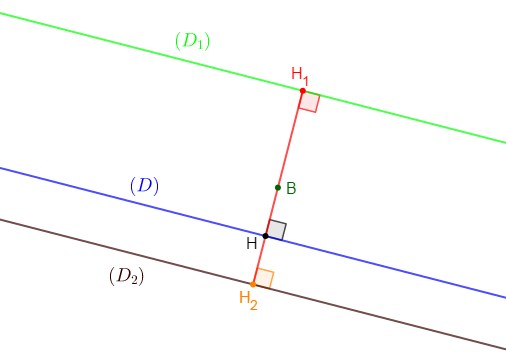
3) Calculons la distance des droites $(D_{1})\ $ et $\ (D_{2})$

 

On a :

 

$\begin{array}{rcl}\text{distance de } (D_{1})\ \text{ et }\ (D_{2})&=&H_{1}H_{2}\\\\&=&H_{1}B+BH_{2}\\\\&=&2\;cm+2\;cm\\\\&=&4\;cm\end{array}$

 

Donc, la distance des droites  $(D_{1})\ $ et $\ (D_{2})$ est de $4\;cm$

 

En effet, les droites $(D)\;;\ (D_{1})\ $ et $\ (D_{2})$ étant parallèles alors, la perpendiculaire à ces droites passant par $B$ coupe $(D)$ en $H\;,\ (D_{1})$ en $H_{1}\ $ et $\ (D_{2})$ en $H_{2}.$

 

4) Calculons la distance de $(D)$ à chacune des droites $(D_{1})$ et $(D_{2})$

 

On a :

 

$\begin{array}{rcl}\text{distance de } (D)\ \text{ à }\ (D_{1})&=&HH_{1}\\\\&=&HB+BH_{1}\\\\&=&1\;cm+2\;cm\\\\&=&3\;cm\end{array}$

 

Ainsi, la distance de  $(D)\ $ à $\ (D_{1})$ est de $3\;cm.$

 

On a :

 

$\begin{array}{rcl}\text{distance de } (D)\ \text{ à }\ (D_{2})&=&HH_{2}\\\\&=&BH_{2}-HB\\\\&=&2\;cm-1\;cm\\\\&=&1\;cm\end{array}$

 

Donc, la distance de  $(D)$ à la droite $(D_{2})$ est égale à $1\;cm.$