Corrigé Exercice 10 : Distances - 4e

 

1) Sur le segment $[AB]$ de longueur $7\;cm$, plaçons les points $I\;,\ C\ $ et $\ O$ tels que : $AI=1\;cm\;;\ AC=2\;cm\ $ et $\ BO=3\;cm.$

 

2) a) Traçons en vert le cercle $\mathcal{C}_{1}(A\;;\ AC).$

 

b) Traçons en rouge le cercle $\mathcal{C}_{2}(B\;;\ BO).$

 

c) Traçons en bleu le cercle $\mathcal{C}_{3}(I\;;\ IO).$

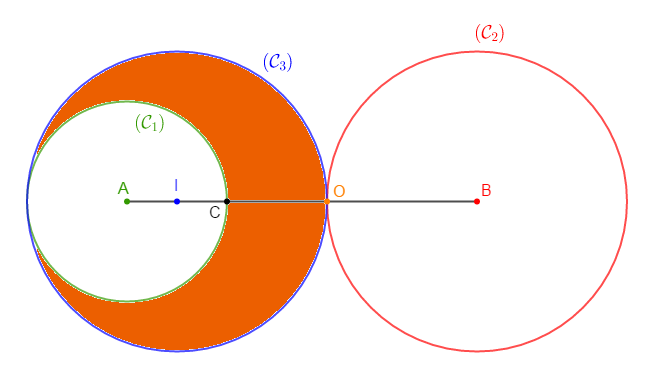
3) Déterminons les positions relatives des cercles :

 

$\mathcal{C}_{1}$ et $\mathcal{C}_{2}\ $ ; $\ \mathcal{C}_{1}$ et $\mathcal{C}_{3}\ $ ; $\ \mathcal{C}_{2}$ et $\mathcal{C}_{3}.$

 

$-\ \ \mathcal{C}_{1}\ $ et $\ \mathcal{C}_{2}$ sont disjoints extérieurement.

 

Pour la justification, on doit vérifier que $AB>AC+BO$

 

En effet, on a : $AB=7\;cm\ $ et $\ AC+BO=2\;cm+3\;cm=5\;cm$

 

Donc, $AB>AC+BO$

 

D'où, les cercles $\mathcal{C}_{1}(A\;;\ AC)\ $ et $\ \mathcal{C}_{2}(B\;;\ BO)$ sont disjoints extérieurement.

 

$-\ \ \mathcal{C}_{1}\ $ et $\ \mathcal{C}_{3}$ sont tangents intérieurement.

 

Pour la justification, on doit vérifier que $AI=|AC-IO|$

 

En effet, on a : $AI=1\;cm$ et comme $I\in[AO]$ alors, $IO+AI=AO$

 

Donc, $IO=AO-AI$

 

Or, $O\in[AB]$ donc, $AO+BO=AB$

 

D'où,

 

$\begin{array}{rcl}AO&=&AB-BO\\\\&=&7\;cm-3\;cm\\\\&=&4\;cm\end{array}$

 

Ainsi, en remplaçant $AO\ $ et $\ AI$ par leur valeur, on obtient :

 

$\begin{array}{rcl} IO&=&AO-AI\\\\&=&4\;cm-1\;cm\\\\&=&3\;cm\end{array}$

 

Par suite,

 

$\begin{array}{rcl} |AC-IO|&=&|2\;cm-3\;cm|\\\\&=&|-1\;cm|\\\\&=&1\;cm\end{array}$

 

D'où, $|AC-IO|=1\;cm$

 

Par conséquent, $AI=|AC-IO|$

 

Ce qui montre que les cercles $\mathcal{C}_{1}(A\;;\ AC)\ $ et $\ \mathcal{C}_{3}(I\;;\ IO)$ sont tangents intérieurement.

 

$-\ \ \mathcal{C}_{2}\ $ et $\ \mathcal{C}_{3}$ sont tangents extérieurement.

 

Pour la justification, on doit vérifier que $IB=IO+BO$

 

En effet, comme $I\in[AB]$ alors, $AI+IB=AB$

 

D'où,

 

$\begin{array}{rcl} IB&=&AB-AI\\\\&=&7\;cm-1\;cm\\\\&=&6\;cm\end{array}$

 

Par ailleurs, $IO=3\;cm\ $ et $\ BO=3\;cm$

 

Donc, $IO+BO=3\;cm+3\;cm=6\;cm$

 

Ainsi, $IB=IO+BO$

 

Ce qui prouve que les cercles $\mathcal{C}_{2}(B\;;\ BO)\ $ et $\ \mathcal{C}_{3}(I\;;\ IO)$ sont tangents extérieurement.

 

4) Colorions l'ensemble des points $M$ du plan tel que : $AM>AC\ $ et $\ MI<IO.$

 

C'est la partie du plan coloriée en orange.

 

Ce sont les points situés à la fois à l'extérieur du cercle $\mathcal{C}_{1}$ et à l'intérieur du cercle $\mathcal{C}_{3}.$

 

En effet,

 

$-\ $ l'ensemble des points $M$ du plan tel que $AM>AC$ est représenté par tous les points du plan situés à l'extérieur du cercle $\mathcal{C}_{1}$

 

$-\ $ l'ensemble des points $M$ du plan tel que $MI<IO$ est représenté par tous les points du plan situés à l'intérieur du cercle $\mathcal{C}_{3}$

 

Ainsi, l'intersection de ces deux ensembles nous donne l'ensemble des points $M$ du plan tel que : $AM>AC\ $ et $\ MI<IO.$

 

Ce qui est alors représenté par la partie coloriée en orange.