Solutions Série d'exercices : Fonctions exponentielle - Ts
Exercice 1: Simplification d'écritures
1) Simplification de \(\dfrac{\mathrm{e}^{4x-2}-\mathrm{e}^{x}}{(\mathrm{e}^{x-1})^{2}-\mathrm{e}^{-x}}\)
On factorise le numérateur et le dénominateur :
Numérateur : \(\mathrm{e}^{x} (\mathrm{e}^{3x-2} - 1)\)
Dénominateur : \(\mathrm{e}^{-x} (\mathrm{e}^{3x-2} - 1)\)
Ainsi, pour \(\mathrm{e}^{3x-2} \neq 1\) (i.e., \(x \neq \frac{2}{3}\)),
\[ \begin{array}{rcl}
\dfrac{\mathrm{e}^{x} (\mathrm{e}^{3x-2} - 1)}{\mathrm{e}^{-x} (\mathrm{e}^{3x-2} - 1)} &=& \dfrac{\mathrm{e}^{x}}{\mathrm{e}^{-x}} \\&=& \mathrm{e}^{2x}.\end{array}\] \(\boxed{\mathrm{e}^{2x}}\)
2) Preuve de \(\begin{array}{rcl}\dfrac{\mathrm{e}^{x}-\mathrm{e}^{-x}}{\mathrm{e}^{x}+\mathrm{e}^{-x}} &=& \dfrac{\mathrm{e}^{2x}-1}{\mathrm{e}^{2x}+1} \\&=& \dfrac{1-\mathrm{e}^{-2x}}{1+\mathrm{e}^{-2x}}\end{array}\)
- Pour la première égalité, multiplier numérateur et dénominateur par \(\mathrm{e}^{x}\) :
\[
\dfrac{(\mathrm{e}^{x} - \mathrm{e}^{-x}) \mathrm{e}^{x}}{(\mathrm{e}^{x} + \mathrm{e}^{-x}) \mathrm{e}^{x}} = \dfrac{\mathrm{e}^{2x} - 1}{\mathrm{e}^{2x} + 1}.
\]
- Pour la seconde égalité, multiplier numérateur et dénominateur par \(\mathrm{e}^{2x}\) :
\[
\dfrac{(1 - \mathrm{e}^{-2x}) \mathrm{e}^{2x}}{(1 + \mathrm{e}^{-2x}) \mathrm{e}^{2x}} = \dfrac{\mathrm{e}^{2x} - 1}{\mathrm{e}^{2x} + 1}.
\]
Les trois expressions sont égales.
3) Preuve de \(\ln(1+\mathrm{e}^{x}) = x + \ln(1+\mathrm{e}^{-x})\)
Partir du côté droit :
\[\begin{array}{rcl} x + \ln(1 + \mathrm{e}^{-x}) &=& \ln(\mathrm{e}^{x}) + \ln(1 + \mathrm{e}^{-x}) \\&=& \ln(\mathrm{e}^{x} (1 + \mathrm{e}^{-x})) \\&=& \ln(\mathrm{e}^{x} + 1) \\&=& \ln(1 + \mathrm{e}^{x}). \end{array} \]
L'égalité est démontrée.
4) Simplification de \(\dfrac{\mathrm{e}^{3+\ln x^{2}}}{\ln 3^{x}}\)
Simplifier le numérateur et le dénominateur :
Numérateur : \(\mathrm{e}^{3 + \ln x^{2}} = \mathrm{e}^{3} \cdot \mathrm{e}^{\ln x^{2}} = \mathrm{e}^{3} x^{2}\)
Dénominateur : \(\ln(3^{x}) = x \ln 3\)
Ainsi, pour \(x \neq 0\),
\[
\dfrac{\mathrm{e}^{3} x^{2}}{x \ln 3} = \dfrac{\mathrm{e}^{3} x}{\ln 3}.
\]
\(\boxed{\dfrac{\mathrm{e}^{3} x}{\ln 3}}\)
Exercice 2: Équations et Inéquations
Résoudre dans \(\mathbb{R}\) :
1) \(\mathrm{e}^{3x} - \mathrm{e}^{x} + 3\mathrm{e}^{x} = 0\)
Simplification : \(\mathrm{e}^{3x} + 2\mathrm{e}^{x} = \mathrm{e}^{x} (\mathrm{e}^{2x} + 2) = 0\).
Comme \(\mathrm{e}^{x} > 0\) et \(\mathrm{e}^{2x} + 2 > 0\), aucune solution.
\(\boxed{\emptyset}\)
2) \(\mathrm{e}^{2x} - 5\mathrm{e}^{x} + 6 = 0\)
Poser \(u = \mathrm{e}^{x}\), alors \(u^2 - 5u + 6 = 0\).
Solutions :
\(u = 2\) ou \(u = 3\), donc \(\mathrm{e}^{x} = 2\) ou \(\mathrm{e}^{x} = 3\), soit \(x = \ln 2\) ou \(x = \ln 3\).
\(\boxed{x = \ln 2}\) ou \(\boxed{x = \ln 3}\)
3) \(\mathrm{e}^{2x} - 3\mathrm{e}^{x} + 2 = 0\)
Poser \(u = \mathrm{e}^{x}\), alors \(u^2 - 3u + 2 = 0\).
Solutions : \(u = 1\) ou \(u = 2\), donc \(\mathrm{e}^{x} = 1\) ou \(\mathrm{e}^{x} = 2\), soit \(x = 0\) ou \(x = \ln 2\).
\(\boxed{x = 0}\) ou \(\boxed{x = \ln 2}\)
4) \(\mathrm{e}^{4x} - 2\mathrm{e}^{3x} - 9\mathrm{e}^{2x} + 18\mathrm{e}^{x} = 0\)
Poser \(u = \mathrm{e}^{x}\), alors \(u^4 - 2u^3 - 9u^2 + 18u = 0\).
Factorisation : \(u(u-2)(u-3)(u+3) = 0\).
Solutions : \(u = 2\) ou \(u = 3\) (car \(u > 0\)), donc \(\mathrm{e}^{x} = 2\) ou \(\mathrm{e}^{x} = 3\), soit \(x = \ln 2\) ou \(x = \ln 3\).
\(\boxed{x = \ln 2}\) ou \(\boxed{x = \ln 3}\)
5) \(6\mathrm{e}^{5x+2} - 7\sqrt{\mathrm{e}^{8x+4}} + \mathrm{e}^{3x+2} = 0\)
Simplifier : \(\sqrt{\mathrm{e}^{8x+4}} = \mathrm{e}^{4x+2}\), donc :
\[
6\mathrm{e}^{5x+2} - 7\mathrm{e}^{4x+2} + \mathrm{e}^{3x+2} = 0.
\]
Factoriser \(\mathrm{e}^{2}\) : \(\mathrm{e}^{2} (6\mathrm{e}^{5x} - 7\mathrm{e}^{4x} + \mathrm{e}^{3x}) = 0\), d'où :
\[
6\mathrm{e}^{5x} - 7\mathrm{e}^{4x} + \mathrm{e}^{3x} = \mathrm{e}^{3x} (6\mathrm{e}^{2x} - 7\mathrm{e}^{x} + 1) = 0.
\]
Ainsi, \(6u^2 - 7u + 1 = 0\) avec \(u = \mathrm{e}^{x}\).
Solutions : \(1\) \(u \frac{1}{6}\), \(\mathrm{e}^{x} 1\)\(\mathrm{e}^{x} \frac{1}{6}\), soit \(x 0\) \(x = -\ln 6\).
\(\boxed{x = 0}\) ou \(\boxed{x = -\ln 6}\)
6) \(\dfrac{\mathrm{e}^{2x-6}}{2-2\mathrm{e}^{x}} = 1\)
Simplifier : \(2 - 2\mathrm{e}^{x} = 2(1 - \mathrm{e}^{x})\), donc :
\[\begin{array}{rcl}
\dfrac{\mathrm{e}^{2x-6}}{2(1 - \mathrm{e}^{x})} &=& 1 \implies \mathrm{e}^{2x-6} \\&=& 2(1 - \mathrm{e}^{x}).\end{array}
\]
Poser \(u = \mathrm{e}^{x} > 0\) et \(u < 1\) (car \(1 - u > 0\)), alors :
\[\begin{array}{rcl}
u^2 \mathrm{e}^{-6} &=& 2(1 - u) \implies u^2 \\&=& 2\mathrm{e}^{6} (1 - u) \implies u^2 + 2\mathrm{e}^{6} u - 2\mathrm{e}^{6} \\&=& 0.\end{array}
\]
Solution positive : \(u = -\mathrm{e}^{6} + \mathrm{e}^{3} \sqrt{\mathrm{e}^{6} + 2}\) (l'autre racine est négative).
Ainsi, \(x = \ln \left( -\mathrm{e}^{6} + \mathrm{e}^{3} \sqrt{\mathrm{e}^{6} + 2} \right)\).
\(\boxed{x = \ln \left( -\mathrm{e}^{6} + \mathrm{e}^{3} \sqrt{\mathrm{e}^{6} + 2} \right)}\)
7) \(\mathrm{e}^{\ln(1-x^{2})} = -2x + 1\)
Domaine : \(1 - x^2 > 0 \iff |x| < 1\).
Équation : \(1 - x^2 = -2x + 1 \implies -x^2 + 2x = 0 \implies x(-x + 2) = 0\), soit \(x = 0\) ou \(x = 2\).
Seule solution dans le domaine : \(x = 0\). \(\boxed{x = 0}\)
8) \((x^{2}-1)\mathrm{e}^{\ln(x-2)} = \ln\mathrm{e}^{(x+1)}\)
Domaine : \(x > 2\).
Simplifier : \(\mathrm{e}^{\ln(x-2)} = x - 2\) et \(\ln(\mathrm{e}^{x+1}) = x + 1\), donc :
\[
(x^2 - 1)(x - 2) = x + 1.
\]
Pour \(x \neq -1\) (mais \(x > 2\)), diviser par \(x + 1\) :
\[
(x - 1)(x - 2) = 1 \implies x^2 - 3x + 1 = 0.
\]
Solutions : \(x = \dfrac{3 \pm \sqrt{5}}{2}\).
Seule solution \(> 2\) : \(x = \dfrac{3 + \sqrt{5}}{2}\).
\(\boxed{x = \dfrac{3 + \sqrt{5}}{2}}\)
9) \(\mathrm{e}^{3x} - \mathrm{e}^{2x} + 3\mathrm{e}^{x} < 0\)
Poser \(u = \mathrm{e}^{x} > 0\), alors \(u^3 - u^2 + 3u < 0\).
Factoriser : \(u(u^2 - u + 3) < 0\).
Comme \(u > 0\) et \(u^2 - u + 3 > 0\) (discriminant négatif), l'inéquation n'est jamais vérifiée.
\(\boxed{\emptyset}\)
10) \(\mathrm{e}^{2x} - 3\mathrm{e}^{x} + 3 < 0\)
Poser \(u = \mathrm{e}^{x} > 0\), alors \(u^2 - 3u + 3 < 0\).
Discriminant négatif et coefficient positif, donc toujours positif, aucune solution.
\(\boxed{\emptyset}\)
11) \(\mathrm{e}^{2x} - 5x + 6 > 0\)
Étudier \(f(x) = \mathrm{e}^{2x} - 5x + 6\).
Dérivée : \(f'(x) = 2\mathrm{e}^{2x} - 5\), minimum en \(x = \frac{1}{2} \ln \frac{5}{2}\), \(f_{\text{min}} > 0\), donc toujours strictement positive.
\(\boxed{\mathbb{R}}\)
12) \(\mathrm{e}^{2x} - 4\mathrm{e}^{x} - 5 > 0\)
Poser \(u = \mathrm{e}^{x} > 0\), alors \(u^2 - 4u - 5 > 0\).
Solutions : \(u < -1\) ou \(u > 5\), mais \(u > 0\), donc \(u > 5\), soit \(\mathrm{e}^{x} > 5\), \(x > \ln 5\).
\(\boxed{\left]\ln 5, +\infty\right[}\)
Exercice 3: Calculs de limites
1) \(f(x) = \dfrac{\mathrm{e}^{x} + \mathrm{e}^{-x}}{\mathrm{e}^{x} - \mathrm{e}^{-x}}\)
- \(\lim\limits_{x \to +\infty} f(x) = 1\)
- \(\lim\limits_{x \to -\infty} f(x) = -1\)
- \(\lim\limits_{x \to 0^+} f(x) = +\infty\)
- \(\lim\limits_{x \to 0^-} f(x) = -\infty\)
\(\boxed{+\infty}\) en \(0^+\), \(\boxed{-\infty}\) en \(0^-\), \(\boxed{1}\) en \(+\infty\), \(\boxed{-1}\) en \(-\infty\)
2) \(f(x) = \dfrac{\mathrm{e}^{x} + \mathrm{e}^{-x}}{x}\)
- \(\lim\limits_{x \to +\infty} f(x) = +\infty\)
- \(\lim\limits_{x \to -\infty} f(x) = -\infty\)
- \(\lim\limits_{x \to 0^+} f(x) = +\infty\)
- \(\lim\limits_{x \to 0^-} f(x) = -\infty\)
\(\boxed{+\infty}\) en \(+\infty\) et \(0^+\), \(\boxed{-\infty}\) en \(-\infty\) et \(0^-\)
3) \(f(x) = \mathrm{e}^{-2x} + 3x\)
- \(\lim\limits_{x \to +\infty} f(x) = +\infty\)
- \(\lim\limits_{x \to -\infty} f(x) = +\infty\)
\(\boxed{+\infty}\) en \(\pm\infty\)
4) \(f(x) = 5\mathrm{e}^{3x} + \mathrm{e}^{2x} - 3\)
- \(\lim\limits_{x \to +\infty} f(x) = +\infty\)
- \(\lim\limits_{x \to -\infty} f(x) = -3\)
\(\boxed{+\infty}\) en \(+\infty\), \(\boxed{-3}\) en \(-\infty\)
5) \(f(x) = \mathrm{e}^{2x} - 4\mathrm{e}^{x} - 5x\)
- \(\lim\limits_{x \to +\infty} f(x) = +\infty\)
- \(\lim\limits_{x \to -\infty} f(x) = +\infty\)
\(\boxed{+\infty}\) en \(\pm\infty\)
6) \(f(x) = \mathrm{e}^{-x^{2}}\)
- \(\lim\limits_{x \to +\infty} f(x) = 0\)
- \(\lim\limits_{x \to -\infty} f(x) = 0\)
- \(\lim\limits_{x \to 0} f(x) = 1\)
\(\boxed{0}\) en \(\pm\infty\), \(\boxed{1}\) en \(0\)
7) \(f(x) = \dfrac{\mathrm{e}^{x} - 1}{x}\)
- \(\lim\limits_{x \to +\infty} f(x) = +\infty\)
- \(\lim\limits_{x \to -\infty} f(x) = 0\)
- \(\lim\limits_{x \to 0} f(x) = 1\)
\(\boxed{+\infty}\) en \(+\infty\), \(\boxed{0}\) en \(-\infty\), \(\boxed{1}\) en \(0\)
8) \(f(x) = x^{2}\mathrm{e}^{2x} - 4x\mathrm{e}^{-x} - 5x - 4\)
- \(\lim\limits_{x \to +\infty} f(x) = +\infty\)
- \(\lim\limits_{x \to -\infty} f(x) = +\infty\)
\(\boxed{+\infty}\) en \(\pm\infty\)
9) \(f(x) = \dfrac{\mathrm{e}^{x} - x\mathrm{e}^{-x}}{\mathrm{e}^{-\sqrt{x}}}\) (domaine \(x \geq 0\))
- \(\lim\limits_{x \to 0^+} f(x) = 1\)
- \(\lim\limits_{x \to +\infty} f(x) = +\infty\)
\(\boxed{1}\) en \(0^+\), \(\boxed{+\infty}\) en \(+\infty\)
10) \(f(x) = \dfrac{\mathrm{e}^{x} - \mathrm{e}^{-x}}{x^{2} + x}\)
- \(\lim\limits_{x \to +\infty} f(x) = +\infty\)
- \(\lim\limits_{x \to -\infty} f(x) = 0\)
- \(\lim\limits_{x \to 0} f(x) = 2\)
- \(\lim\limits_{x \to -1^+} f(x) = +\infty\)
- \(\lim\limits_{x \to -1^-} f(x) = -\infty\)
\(\boxed{+\infty}\) en \(+\infty\) et \(-1^+\), \(\boxed{0}\) en \(-\infty\), \(\boxed{2}\) en \(0\), \(\boxed{-\infty}\) en \(-1^-\)
11) \(f(x) = \ln(1 + \mathrm{e}^{x})\)
- \(\lim\limits_{x \to +\infty} f(x) = +\infty\)
- \(\lim\limits_{x \to -\infty} f(x) = 0\)
\(\boxed{+\infty}\) en \(+\infty\), \(\boxed{0}\) en \(-\infty\)
12) \(f(x) = \sqrt{x-3} \ln(x-3)^{2}\) (domaine \(x > 3\))
- \(\lim\limits_{x \to 3^+} f(x) = 0\)
- \(\lim\limits_{x \to +\infty} f(x) = +\infty\)
\(\boxed{0}\) en \(3^+\), \(\boxed{+\infty}\) en \(+\infty\)
13) \(f(x) = \mathrm{e}^{x} \ln |x|\)
- \(\lim\limits_{x \to 0} f(x) = -\infty\)
- \(\lim\limits_{x \to +\infty} f(x) = +\infty\)
- \(\lim\limits_{x \to -\infty} f(x) = 0\)
\(\boxed{-\infty}\) en \(0\), \(\boxed{+\infty}\) en \(+\infty\), \(\boxed{0}\) en \(-\infty\)
14) \(f(x) = \dfrac{\ln(x^{2} - x + 1)}{x + 1}\)
- \(\lim\limits_{x \to +\infty} f(x) = 0\)
- \(\lim\limits_{x \to -\infty} f(x) = 0\)
- \(\lim\limits_{x \to -1^+} f(x) = +\infty\)
- \(\lim\limits_{x \to -1^-} f(x) = -\infty\)
\(\boxed{0}\) en \(\pm\infty\), \(\boxed{+\infty}\) en \(-1^+\), \(\boxed{-\infty}\) en \(-1^-\)
15) \(f(x) = \dfrac{\ln(x^{2} + 1)}{|x| + 1} \mathrm{e}^{-x}\)
- \(\lim\limits_{x \to +\infty} f(x) = 0\)
- \(\lim\limits_{x \to -\infty} f(x) = +\infty\)
- \(\lim\limits_{x \to 0} f(x) = 0\)
\(\boxed{0}\) en \(+\infty\) et \(0\), \(\boxed{+\infty}\) en \(-\infty\)
Exercice 4: Dérivées
1) \( f(x) = (x^{2} - 5x + 1) e^{3x - 1} \)
La fonction est un produit de \( u(x) = x^2 - 5x + 1 \) et \( v(x) = e^{3x - 1} \).
- \( u'(x) = 2x - 5 \)
- \( v'(x) = 3e^{3x - 1} \) (par dérivation de l'exponentielle composée)
Dérivée du produit : \( f'(x) = u'v + uv' = (2x - 5)e^{3x - 1} + (x^2 - 5x + 1) \cdot 3e^{3x - 1} \).
En factorisant \( e^{3x - 1} \) :
\[ f'(x) = e^{3x - 1} \left[ (2x - 5) + 3(x^2 - 5x + 1) \right] = e^{3x - 1} (3x^2 - 13x - 2) \]
2) \( f(x) = e^{-x^{2}} \)
La fonction est composée : soit \( u = -x^2 \), alors \( f(x) = e^u \).
- \( u'(x) = -2x \)
- \( f'(x) = e^u \cdot u'(x) = e^{-x^2} \cdot (-2x) = -2x e^{-x^2} \)
3) \( f(x) = \ln(1 + e^{x}) \)
La fonction est composée : soit \( u = 1 + e^x \), alors \( f(x) = \ln u \).
- \( u'(x) = e^x \)
- \( f'(x) = \frac{1}{u} \cdot u'(x) = \frac{1}{1 + e^x} \cdot e^x = \frac{e^x}{1 + e^x} \)
4)
Pour calculer la dérivée de la fonction \( f(x) = \exp\left(\dfrac{1}{x^2 - x}\right) \), on utilise la règle de la chaîne. Soit \( u = \dfrac{1}{x^2 - x} \).
Alors, \( f(x) = \exp(u) \).
La dérivée de \( \exp(u) \) par rapport à \( x \) est \( \exp(u) \cdot u'(x) \).
Maintenant, on calcule \( u'(x) \). On a \( u = (x^2 - x)^{-1} \). En utilisant la dérivée d'une puissance et la règle de la chaîne :
\[
u'(x) = -1 \cdot (x^2 - x)^{-2} \cdot (2x - 1) = -\dfrac{2x - 1}{(x^2 - x)^2}.
\]
Ainsi,
\[
f'(x) = \exp\left(\dfrac{1}{x^2 - x}\right) \cdot \left( -\dfrac{2x - 1}{(x^2 - x)^2} \right) = -\dfrac{2x - 1}{(x^2 - x)^2} \exp\left(\dfrac{1}{x^2 - x}\right).
\]
La fonction est définie pour \( x \neq 0 \) et \( x \neq 1 \), et l'expression de la dérivée est valide dans ce domaine.
\[
\boxed{f'(x) = -\dfrac{2x - 1}{(x^2 - x)^2} \exp\left(\dfrac{1}{x^2 - x}\right)}
\]
5) \( f(x) = \dfrac{e^{x} + e^{-x}}{e^{x} - e^{-x}} \)
La fonction est un quotient : soit \( u = e^x + e^{-x} \), \( v = e^x - e^{-x} \), alors \( f(x) = \frac{u}{v} \).
- \( u' = e^x - e^{-x} = v \)
- \( v' = e^x + e^{-x} = u \)
Dérivée du quotient : \( f'(x) = \frac{u'v - uv'}{v^2} = \frac{v \cdot v - u \cdot u}{v^2} = \frac{v^2 - u^2}{v^2} \).
Calcul de \( v^2 - u^2 \):
\[\begin{array}{rcl} u^2 &=& (e^x + e^{-x})^2 \\&=& e^{2x} + 2 + e^{-2x}, \quad v^2 \\&=& (e^x - e^{-x})^2 \\&=& e^{2x} - 2 + e^{-2x}\end{array} \]
\[ \begin{array}{rcl}v^2 - u^2 &=& (e^{2x} - 2 + e^{-2x}) - (e^{2x} + 2 + e^{-2x}) \\&=& -4 \end{array}\]
Ainsi, \( f'(x) = \frac{-4}{v^2} = -\frac{4}{(e^x - e^{-x})^2} \)
6) \( f(x) = \dfrac{e^{x} - 1}{x} \)
La fonction est un quotient : soit \( u = e^x - 1 \), \( v = x \), alors \( f(x) = \frac{u}{v} \).
- \( u' = e^x \)
- \( v' = 1 \)
Dérivée du quotient : \(\begin{array}{rcl} f'(x) &=& \frac{u'v - uv'}{v^2} \\&=& \frac{e^x \cdot x - (e^x - 1) \cdot 1}{x^2} \\&=& \frac{x e^x - e^x + 1}{x^2}\end{array} \).
On peut aussi écrire : \( f'(x) = \frac{e^x (x - 1) + 1}{x^2} \)
Exercice 5: Primitives
Primitives des fonctions données
1) \( f(x) = e^{-2x-1} \)
La primitive d'une fonction exponentielle de la forme \( e^{ax + b} \) est \( \frac{1}{a} e^{ax + b} + C \).
Ici, \( a = -2 \) et \( b = -1 \), donc :
\[ \int e^{-2x-1} dx = -\frac{1}{2} e^{-2x-1} + C \]
2) \( f(x) = (-x + 2) e^{-x^{2} + 4x - 1} \)
On reconnaît que le terme \( -x + 2 \) est proportionnel à la dérivée de l'exposant \( -x^2 + 4x - 1 \).
Soit \( u = -x^2 + 4x - 1 \), alors \( u' = -2x + 4 = 2(-x + 2) \).
Ainsi :
\[\begin{array}{rcl} f(x) &=& (-x + 2) e^u \\&=& \frac{1}{2} \cdot 2(-x + 2) e^u \\&=& \frac{1}{2} u' e^u \end{array}\]
La primitive est donc :
\[ \int f(x) dx = \frac{1}{2} e^{-x^{2} + 4x - 1} + C \]
3) \( f(x) = \sin x e^{\cos x} \)
On reconnaît que \( \sin x \) est la dérivée de \( -\cos x \) à un signe près.
Soit \( u = \cos x \), alors \( u' = -\sin x \), donc :
\[ f(x) = \sin x e^{\cos x} = - (-\sin x) e^u = - u' e^u \]
La primitive est donc :
\[ \int f(x) dx = -e^{\cos x} + C \]
4) \( f(x) = \dfrac{e^{x} + e^{-x}}{e^{x} - e^{-x}} \)
On reconnaît que le numérateur est la dérivée du dénominateur.
Soit \( u = e^x - e^{-x} \), alors \( u' = e^x + e^{-x} \). Ainsi :
\[ f(x) = \frac{u'}{u} \]
La primitive de \( \frac{u'}{u} \) est \( \ln |u| + C \), donc :
\[ \int f(x) dx = \ln \left| e^{x} - e^{-x} \right| + C \]
La valeur absolue est nécessaire car \( e^x - e^{-x} \) peut être négatif (pour \( x < 0 \)).
Exercice 6 Étude de fonctions
1) $f(x) = x e^x$
Domaine : $\mathbb{R}$
Limites :
$\lim\limits_{x \to -\infty} x e^x = 0$ (car $e^x \to 0$ + $x \to -\infty$, donc forme indéterminée → changement de variable : $u = -x \Rightarrow ue^{-u} \to 0$)
$\lim\limits_{x \to +\infty} x e^x = +\infty$
Dérivée :
$$
f'(x) = e^x + x e^x = e^x(1 + x)
$$
Sens de variation :
$f'(x) > 0$ si $x > -1$
$f'(x) < 0$ si $x < -1$
Minimum local en $x = -1$, $f(-1) = -\dfrac{1}{e}$
Tableau de variation :
$$
\begin{array}{c|ccc|c}
x & -\infty & & -1 & +\infty \\
\hline
f'(x) & & - & 0 & + \\
\hline
f(x) & 0 & \searrow & -\frac{1}{e} & \nearrow & +\infty
\end{array}
$$

2) $f(x) = x^3 e^x$
Domaine : $\mathbb{R}$
Limites :
$x \to -\infty$: forme $-\infty \cdot 0$. En posant $u = x^3, v = e^x$, on sait que $e^x$ domine $x^3$ donc $f(x) \to 0$
$x \to +\infty$: $f(x) \to +\infty$
Dérivée :
$$
f'(x) = (3x^2 + x^3) e^x = x^2(3 + x) e^x
$$
Sens de variation :
$f'(x) = 0$ si $x = 0$ ou $x = -3$
Signe de $f'(x)$ :
Négatif sur $(-\infty, -3)$
Positif sur $(-3, 0)$ (car $3+x > 0$)
Positif sur $(0, +\infty)$
Tableau de variation :
$$
\begin{array}{c|cccccc}
x & -\infty & & -3 & & 0 & +\infty \\
\hline
f'(x) & & - & 0 & + & 0 & + \\
\hline
f(x) & 0 & \searrow & f(-3) & \nearrow & 0 & \nearrow
\end{array}
$$

3) $f(x) = \dfrac{e^x}{x}$
Domaine : $\mathbb{R} \setminus \{0\}$
Limites :
$x \to 0^+ \Rightarrow +\infty$, $x \to 0^- \Rightarrow -\infty$
$x \to +\infty \Rightarrow +\infty$, $x \to -\infty \Rightarrow 0^-$
Dérivée :
$$
f'(x) = \frac{e^x x - e^x}{x^2} = \frac{e^x(x - 1)}{x^2}
$$
Sens de variation :
Dérivée s'annule en $x = 1$
$f'(x) > 0$ si $x > 1$ ou $x < 0$
$f'(x) < 0$ pour $0 < x < 1$
Asymptotes :
Asymptote verticale en $x = 0$

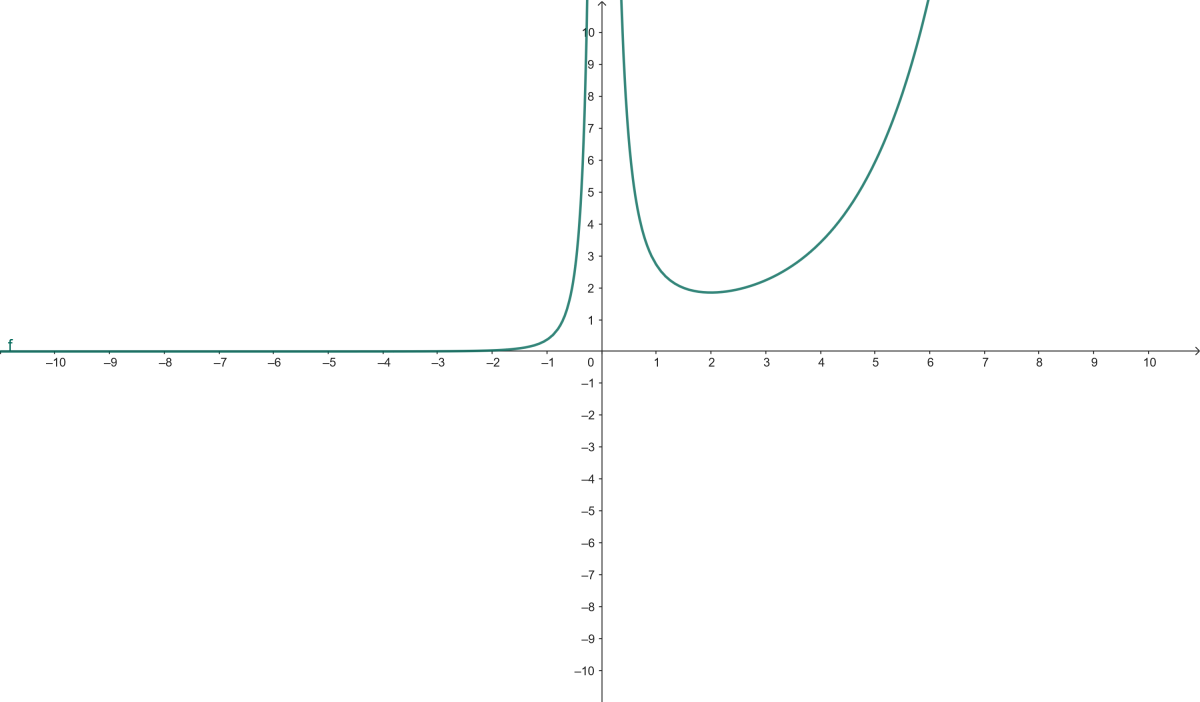
4) $f(x) = \dfrac{e^x}{x^2}$
Domaine : $\mathbb{R} \setminus \{0\}$
Limites :
$x \to 0^+ \Rightarrow +\infty$, $x \to 0^- \Rightarrow +\infty$
$x \to -\infty \Rightarrow 0^+$, $x \to +\infty \Rightarrow +\infty$
Dérivée :
$$
f'(x) = \frac{e^x x^2 - 2x e^x}{x^4} = \frac{e^x(x^2 - 2x)}{x^4}
= \frac{e^x x(x - 2)}{x^4} = \frac{e^x(x - 2)}{x^3}
$$
Étude du signe de $f'(x)$ :
Nul en $x = 2$
$f'(x) > 0$ pour $x > 2$ et $x < 0$
$f'(x) < 0$ pour $0 < x < 2$
5) $f(x) = \dfrac{x}{e^x}$
Domaine : $\mathbb{R}$
Limites :
$x \to -\infty \Rightarrow \dfrac{-\infty}{0^+} = -\infty$
$x \to +\infty \Rightarrow \dfrac{+\infty}{+\infty}$ → $f(x) \to 0$
Dérivée :
$$
f'(x) = \frac{e^x - x e^x}{e^{2x}} = \frac{(1 - x)e^x}{e^{2x}} = \frac{1 - x}{e^x}
$$
Signe de $f'(x)$ :
$f'(x) > 0$ si $x < 1$, $f'(x) < 0$ si $x > 1$
Maximum en $x = 1$, $f(1) = \dfrac{1}{e}$

6) $f(x) = x^2 e^x$
Domaine : $\mathbb{R}$
Limites :
$x \to -\infty \Rightarrow 0$ (exponentielle domine)
$x \to +\infty \Rightarrow +\infty$
Dérivée :
$$
f'(x) = (2x + x^2)e^x = x(2 + x)e^x
$$
Étude du signe de $f'(x)$ :
$f'(x) < 0$ pour $x < -2$
$f'(x) > 0$ pour $x > -2$
Minimum local en $x = -2$

7) $f(x) = e^{\frac{x+1}{x^2}}$
Domaine : $\mathbb{R} \setminus \{0\}$
Limites :
Analyse de $\frac{x+1}{x^2}$
$x \to 0^+ \Rightarrow +\infty \Rightarrow f(x) \to +\infty$
$x \to 0^- \Rightarrow -\infty \Rightarrow f(x) \to 0$
$x \to \pm \infty \Rightarrow \frac{1}{x} + \frac{1}{x^2} \to 0 \Rightarrow f(x) \to 1$

Ajouter un commentaire