Corrigé Bac Maths S1 S3 1er groupe 2017

Exercice1

1.  $A(0, 0, 0), B(1, 0, 0), C(1, 1, 0), D(0, 1, 0), E(0, 0, 1), F(1, 1, 0), G(1, 1, 1), H(1, 0, 1)$

a. Le vecteur $\vec{BD} =\vec{AD} -\vec{AB}$ a pour coordonnées $(-1, 1, 0)$ c’est à dire $\vec{BD} = -\vec{i} +\vec{j}$

Le vecteur $\vec{BG} =\vec{AG}-\vec{AB}$ a pour coordonnées $(0, 1, 1)$ c’est à dire $\vec{BD} =\vec{j} +\vec{k}$

Donc $BD ∧ BG = (-\vec{i} +\vec{j} ) ∧ (\vec{j} +\vec{k} ) = -\vec{k} +\vec{j} +\vec{i}$ .

Les coordonnées de $\vec{BD}∧\vec{BG}$ sont $(1, 1, -1)$.
b. Le plan $(BGD)$ peut être défini comme le plan passant par $B$ et de vecteur normal $\vec{n} = \vec{BD} ∧ \vec{BG}$.
Un point P de coordonnées $(x, z, y)$ appartient donc à ce plan si et seulement si $\vec{n}. \vec{BP} = 0$
c’est à dire $1(x - 1) + 1(y - 0) - 1(z - 0) = 0$ ou $x + y - z - 1 = 0$.
Cette dernière équation est donc une équation cartésienne de $(BGD)$.
c. On a $\vec{EC} =\vec{n}$ qui est normal au plan $(BGD)$, donc la droite (EC) est bien perpendiculaire
au plan $(BGD)$.

2.  La distance du point $C$ au plan $(BGE)$ est $r =\dfrac{|xC + yC - zC - 1|}{1^2+1^1+1^2}=\dfrac{\sqrt{3}}{3}$. Un point $P$ de

coordonnées (x, z, y) appartient donc à la sphère S si et seulement si $CP^2 = r^2$
c’est à dire($x - 1)^2 + (y - 1)^2 + (z - 0)^2 =\dfrac{1}{3}$ ou $(x - 1)^2 + (y - 1)^2 + z^2 =\dfrac{1}{3}$.
Cette dernière équation est donc une équation cartésienne de $S$.

3.  A tout $α$ appartenant à l’intervalle $[0, 1]$ on associe le point $M$ de coordonnées $(α, α, 1-α)$.

a. Pour que $M$ soit un point du segment $[EC]$, il faut et il suffit qu’il soit barycentre de ces
deux points avec des poids positifs de somme $1$.
cherchons donc $t \in [0, 1]$ tel que $\vec{AM} = (1 - t)\vec{AE} + t\vec{AC}$ c’est à dire
$(α, α, 1 - α) = (1 - t)(0, 0, 1) + t(1, 1, 0) = (t,t, 1 - t)$
Donc t = α.
b. Les points $E$ et $C$ appartiennent au plan médiateur du segment $[BD]$ ; donc ce plan
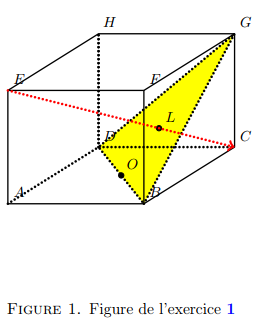
contient la droite $(EC)$ et partant le point $M$ : $MBD$ est un triangle isocèle en $M$. La distance
$d(α)$ de $M$ à cette droite est donc égale à $MO$, $O$ étant le milieu de $[BD]$. Les coordonnées de
$O$ sont $(1/2, 1/2, 0)$.
$d(α) = MO =\sqrt{(α -\dfrac{1}{2})^2 + (α -\dfrac{1}{2})^2 + (1 - α - 0)^2} =\sqrt{3α^2 - 4α +\dfrac{3}{2}}$.

c) Pour que la distance de $M$ à la droite $(BD)$ soit minimale il faut et il suffit que la fonction d ait un minimum.

$d′(x) =\dfrac{3α - 2}{d(α)}$

. Voici le tableau de variations de d)

Pour que la distance soit minimale il faut et il suffit que α soit égal à $2/3$.

La distance minimale est alors égale à $\sqrt{1/6}$ et les coordonnées de $L$ sont $(\frac{2}{3},\frac{2}{3},\frac{1}{3})$

d) Le centre de gravité du triangle $BGD$ a pour coordonnées
$\dfrac{1}{3}(x_B + x_G + x_D, y_B + y_G + y_D, z_B + z_G + z_D) =\dfrac{1}{3}(2, 2, 1)$ = coordonnées de $L$.

Le centre de gravité de $BGD$ est bien $L$.

4.  a. Soit $P$ un point de coordonnées ($x, y, z)$ et $P′$ un point de coordonnées $(x′, y′, z′)$.

$P′ = h(P) ⇔ \vec{EP′} = α\vec{EP}$
$\quad⇔ (x′, y′, z′ - 1) = α(x, y, z - 1)$
$\quad⇔ \left\{     \begin{array}{rl}       x' = αx\\       y' = αy \\       z' = αz+1-α\\   \end{array}     \right.$

Ce dernier système est l’expression analytique de $h$.
b. Posons $h(C) = C'$. D’après la question précédente, $C′$ a pour coordonnées :
$(k x_C, k y_C, z_C + 1 - k) = (k, k, 1 - α)$ = coordonnées de $M$;
donc $M = C′ = h(C)$.
c. S$′$ est la sphère de centre $h(C) = M$ et de rayon $|k|r$.
Un point $P$ de coordonnées $(x, z, y)$ appartient donc à la sphère $S′$
si et seulement si $MP^2 = k^2r^2$ c’est à dire $(x-k)^2+(y-k)^2+(z-1+k)^2 =\dfrac{1}{3}k^2$.
Cette dernière équation est donc une équation cartésienne de $S′$.

Exercice 2 (4 points)

Soit $a$ un entier naturel non nul et $(u_n)_{n\in \mathbb{N}}$ la suite définie par :
$u_n = pgcd(n, a).$

1.  a. $u_0 = pgcd (0, 15) = 15$, $u_1 = pgcd (1, 15) = 1$, $u_2 = pgcd (2, 15) = 1$.

b. Pour $a = 4$, $u_m = u_n = 2$ signifie $pgcd (m, 4) = pgcd (n, 4) = 2$.
$m$ et $n$ sont donc des nombres paires non multiples de $4$.
Il existe donc des entiers naturels impairs $2m′ + 1$ et $2n′ + 1$ tels que $m = 2(2m′ + 1)$ et $n = 2(2n′ + 1)$.
Alors $m + n = 4(m′ + n′ + 1)$, puis $pgcd (m + n, 4) = 4$ c’est à dire $u_{m+n} = 4$.

2.  a. Soit $b$ un entier naturel.

Démontrer que pour tout entier relatif $q$ on a : $pgcd(a, b) = pgcd(a, b − qa)$.
Soit $d$ un entier.
Si $d$ est un diviseur commun de $a$ et $b$, il existe deux entiers $m$ et $n$ tels que $a = dm$ et $b = dn$.
Alors $b − qa = d(n − qm)$. Donc $d$ est un diviseur commun de $a$ et $b − qa$.
Réciproquement, si $d$ est un diviseur commun de $a$ et $b − qa$, il existe deux entiers $m′$
et $n′$ tels que $a = dm′$ et $b − qa = dn′$.
Alors $b = (b − qa) + qa = d(n′ + qm′)$. Donc $d$ est un diviseur commun de $a$ et $b$.
${a, b}$ et ${a, b − qa}$ ayant les mêmes diviseurs commun ont le même pgcd.
b. $u_0 = pgcd (0, a) = a$ et $u_a = pgcd (a, a) = a$.

c.
$$\begin{array} {rcl} u_{n+a} &= &pgcd (a, n + a)\\ & = &pgcd (a, n) \text{ d’apreès le a. avec }b = n + a \text{ et } q = −1\\ &= &un \end{array}$$ .
Nous venons de démontrer que la suite $(un)$ est périodique et $a$ est une période.
3. $n = 15^{21} + 2 = 2 + 15m$ avec $m = 15^{20}$ donc
$$\begin{array} {rcl}  u_n &=& u2+15m\\ & = & u2 \ \text{car} \ 15 \ \text{est une période de } (u_n)\\ &= &pgcd (2, 15)\\ &=&1  \end{array}$$

Problème

Partie A

1.  a.

La fonction $ϕ: x\mapsto \ln x - x$ est définie et continue sur $\mathbb{R}^*+$.

Elle est dérivable et $∀ x ∈ \mathbb{R}^*+$, $ϕ′(x)=\dfrac{1}{x}- 1 =\dfrac{1 - x}{x}$.

Voici son tableau de variations.

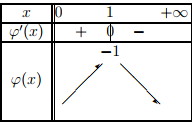
On y voit clairement que le maximum de $ϕ$ est $-1$ donc $∀x ∈ \mathbb{R}^*+$, $\ln x - x ≤ -1 < 0$.
Remarquer qu’on n’a pas besoin des limites de $ϕ$ aux bornes de son ensemble de définition.
b. L’application $f_n$ est dérivable sur $\mathbb{R}$ et $∀x ∈ \mathbb{R}$, $f_n′(x) = 1+e^x$.
La dérivée étant strictement positive, la fonction $f_n$ est strictement croissante.
$\lim\limits_{x\to +∞} f_n(x) = +∞$ et $\lim\limits_{x\to -∞} f_n(x) = -∞$ car $\lim\limits_{x\to -∞} e^x)= 0$

Par conséquent, $f_n$ réalise une bijection de $\mathbb{R}$ sur $f_n(\mathbb{R}) = \mathbb{R}$, et l’équation $f_n(x) = 0$ ( c’est
à dire l’équation ($E_n$)) admet une solution unique ( dépendant naturellement $n$).
$f_n(\ln n) = \ln n > 0$ et $f_n(\ln\dfrac{n}{2}=\ln\dfrac{n}{2}-\dfrac{n}{2}< 0$ d’après le a.
Ainsi $f_n(\ln n) × f_n(\ln\dfrac{n}{2}< 0$, donc un appartient à $]\ln(n/2), \ln n[$

c. La relation $u_n > \ln \dfrac{n}{2}\xrightarrow{n→+∞}$ entrainent $\lim\limits_{n\to +∞} u_n = +∞$
De $\ln \dfrac{n}{2}< u_n ≤ \ln n$ on tire :
- En divisant par $n$,$\dfrac{\ln n}{n}-\dfrac{\ln 2}{n}<\dfrac{u_n}{n}≤\dfrac{\ln n}{n}$
et comme les suites minorante et majorante ont 0 comme limite commune, le théorème des gendarmes permet d’écrire $\lim\limits_{n\to +∞}\dfrac{u_n}{n}=0$.
- En divisant par $\ln n$, $1 - \dfrac{\ln 2}{\ln n}<\dfrac{u_n}{n}≤ \dfrac{\ln n}{n}$ et comme les suites minorante et majorante
(suite constante) ont $1$ comme limite commune, le théeorème des gendarmes permet d’écrire
$\lim\limits_{n\to +∞}\dfrac{u_n}{\ln n}=1$

d. Pour $n = 1$, on a $u_1 + e^u1 - 1 = 0$, donc $u_1 = 0$.

2.  a. On a, en suivant la remarque

$\dfrac{e^u_{n+1}}{e^u_n}=\dfrac{n + 1-u_{n+1}}{n-u_n}=\dfrac{n+1}{n}\dfrac{1-\dfrac{u_{n+1}}{n+1}}{1-\dfrac{u_n}{n}}$
Le premier facteur a pour limite $1$ et le deuxième facteur, compte tenu du fait que
$\lim\limits_{n\to +∞}\dfrac{u_n}{n}=0$, a aussi pour limite 1. Donc lim $\lim\limits_{n\to +∞}\dfrac{e^u_{n+1}}{e^u_n}=1$
Comme $\dfrac{e^u_{n+1}}{e^u_n}$= e^{u_{n+1}-un} a pour limite 1, on a bien $\lim\limits_{n\to +∞}u_{n+1}-u_n=1$

b. On a $f_n(u_n) = 0$ et en suivant la remarque $f_n(u_n+1) = u_{n+1} + e^{u_{n+1}} + n = (n + 1) - n = 1$.
la relation $f_n(u_n) = 0 < 1 = f_n(u_{n+1})$ et la stricte croissance de l’application $f_n$ entraînent
$u_n < u_{n+1}$ ; la suite ($u_n$) est donc strictement croissante.
c.
$$\begin{array} {lcl} A_n &=&\int_{u_n}^{u_{n+1}} f_n(x) dx\\ &=&[\frac{1}{2}x^2+e^x-nx]_{u_n}^{u_{n+1}}\\ &=&\frac{1}{2}{u_{n+1}}^2+e^{u_{n+1}}-nu_{n+1}-(\frac{1}{2}{u_n}^2+e^{u_n}) \text{puis, suivant la remarque}\\ &=&\frac{1}{2}{u_{n+1}}^2+(n+1)-u_{n+1}-nu_{n+1}-(\frac{1}{2}{u_n}^2+n-u_n-nu_n)\\ &=&\frac{1}{2}({u_{n+1}}^2-{u_n}^2)-(n+1)(u_{n+1}-u_n)+1 \end{array}$$

Puisque l’application $f_n$ est croissante, on a pour tout $t$ appartenant à $[u_n, u_{n+1}]$,
$f_n(u_n) ≤ f_n(t) ≤ f_n(u_{n+1})$ c’est à dire $0 ≤ f_n(t) ≤ 1$ puis par intégration
$0 ≤ An ≤\int_{u_n}^{u_{n+1}} 1 dx = u_{n+1} - u_n$.
comme les suites minorante (suite constante égale à $0$) et majorante ont $0$ comme limite commune, le théorème des gendarmes permet d’écrire
$\lim\limits_{n\to +∞}A_n=0$

3.  a. La fonction $ψ : x \mapsto \ln(1 + x)$ est définie, continue et dérivable sur son ensemble de

définition $D =] - 1, +∞[$. Sa dérivée est l’application $x \mapsto \frac{1}{1 + x}$, elle vaut $1$ au point $0$. Donc
$\lim\limits_{h\to 0} \frac{ψ(h) - ψ(0)}{h}- 1 = 0$. En posant
$ε(h) =\frac{ψ(h) - ψ(0)}{h}- 1$ si $h \neq 0$ et $ε(0) = 0$,
on bien $ψ(h) = h + hε(h)$ pour tout $h$ appartenant à $D$.
b. On sait d’après le résultat de la question 1 que $\frac{un}{\ln n}$ a pour limite $1$, donc $(α_n)$ a pour
limite $0$.
On déduit de $u_n = \ln n + α_n \ln n$ et en suivant la remarque :
$$\begin{array} {lcl}  e^u_n & = & n - u_n = n - \ln n - α_n \ln n \\  ⇒ u_n & = & \ln( n - \ln n - α_n \ln n) \\  & = & \ln n + \ln (1 - \frac{\ln n}{n}- α_n\frac{\ln n}{n}\\  & = & \ln n + \ln(1 + yn)  \end{array}$$

Puisque la suite $(y_n)$ a pour limite $0$, on peut écrire, d’aprés la question précédente :
$u_n = \ln n + y_n + y_nε_n$, $(ε_n)$ étant une suite ayant pour limite $0$.
Donc $$\begin{array} {lcl} un &=& \ln n - \dfrac{\ln n}{n}- αn\dfrac{\ln n}{n}-(-\dfrac{\ln n}{n}- α_n\dfrac{\ln n}{n})ε_n\\ &= &\ln n -\dfrac{\ln n}{n}+ β_n\dfrac{\ln n}{n} \quad \text{avec} \quad  β_n = -α_n + ε_n + αnε_n \end{array}$$

Partie B

1.  a.

On a d’après l’indication de la première partie,
$e^u_2 = 2 - u_2$ c’est à dire $u_2 = \ln(2 - u_2) = g(u_2)$.
$u_2$ est un point fixe de $g$.
Or $g$ est dérivable dans $[a, b]$ et $∀x ∈ [a, b]$, $g′(x) = -\dfrac{1}{2 - x}$.
La dérivée de $g$ étant $< 0$, g est strictement décroissante ;donc $u_2$ est le seul point fixe de $g$.
$f_2(b) = b + e^b - 2 =\dfrac{2}{3}\ln 2 + 2^{2/3} - 2 \sim 0.46 > 0$.
$f_2(a) = f_2(\ln(2 - b)) = \ln(2 - b) + 2 - b - 2 = ln(2 - b) - b \sim -0.31 < 0$.
Puisque $f_2(a)$ et $f_2(a)$ sont de signe contraire, $u_2$ appartient à $]a, b[$
b. On a déjà montré que g est dérivable sur $I$ et $∀x ∈ I$, $g′(x) = -\dfrac{1}{2 - x}$.
Alors $|g′(x)| =\dfrac{1}{2 - x}$.
L’application $p : x \mapsto \dfrac{1}{2 - x}$ est dérivable sur $I$ et sa dérivée $x \mapsto \dfrac{1}{(2 - x)^2}$
est $> 0$ sur $I$. p est donc croissante. Par conséquent
$∀x ∈ I, x ≤ b =⇒ p(x) ≤ p(b)$ c’est à dire $|g′(x)| ≤ |g′(b)|$
Voici le théeoréme appelé Inégalité des accroissements finis qui permet d’en déduire que
$∀x, y ∈ I, |g(x) - g(y)| ≤ |g′(b)| |x - y|$.
Soit $ϕ$ une application définie sur un intervalle $J = [u, v]$ à valeurs dans $\mathbb{R}$.
On suppose que ϕ est continue sur J, dérivable sur $]u, v[$ et il existe un réel $k ≥ 0$ vérifiant
$∀x ∈]u, v[, |ϕ′(x)| ≤ k$
Alors
$∀x, y ∈ J, |ϕ(x) - ϕ(y)| ≤ k |x - y|$.
c. $g$ étant continue et décroissante, $g([a, b]) = [g(b), g(a)] = [a, g(a)]$.
Pour que $g(I) \subset I$, il suffit que $g(a) ≤ b$ c’est à dire $g[g(b)] ≤ b$,
ce que montre un calcul direct (on trouve $b - g[g(b)] \sim 0.011)$

2.  a. Pour répondre à la question, puisque $I$ est contenu dans l’ensemble de définition de $g$,

il suffit de démontrer par récurrence la propriété $P_n$ : " $a_n$ existe et $an \in I$ ".
$a0 = b$ existe et $\in I$, $P_0$ est donc vraie.
Si $P_n$ est vraie pour un entier donnée $n$ alors $a_n$ existe et
$$\begin{array} {lcl} an \in I & ⇒ &g(an) \in I \text{ car } g(I) \subset I \\ &⇔ &an+1 \in I \end{array}$$
$P_{n+1}$ est donc vraie.
b. Démontrons par récurrence la propriété Dn : " $|an - u2| ≤ |g′(b)|^n(b - a)$".
On a $|a_0 - u_2| ≤ b - a = |g′(b)|^0(b - a)$, $D_0$ est donc vraie.
Si $D_n$ est vraie pour un entier donnée $n$, on a :
$$\begin{array} {rcl} &|g(a_n) - g(u_2)|& ≤& |g′(b)||a_n - u_2| \text{ d’aprés la question 1. b.}\\ ⇔ &|a_{n+1} - u_2|& ≤ &|g′(b)||a_n - u_2|\\ & &≤ &|g′(b)||g′(b)|^n(b - a) \text{ car } D_n \text{ est supposée vraie}\\ & &=& |g′(b)|n+1(b - a) \end{array}$$
$D_{n+1}$ est donc vraie.

$k = |g′(b)| =\dfrac{1}{2 - b}\sim 0.65 \text{ est } < 1 \text{ donc } \lim\limits_{n\to +∞}k^n=0$ et la propriété $D_n$ et le théorème des gendarmes entrainent $\lim\limits_{n\to +∞}|a_n - u_2| = 0$.

La suite $(a_n)$ est donc convergente et de limite $u_2$.

c. Pour que $a_n$ soit une valeur approchée de $u_2$ à $10^{-3}$, il suffit que $k^n(b - a) \text{ soit }≤ 10^{-3}$ c’est à dire $n ≥\dfrac{3 \ln 10 + \ln(b - a)}{\ln(2 - b)}\sim 8.02$.

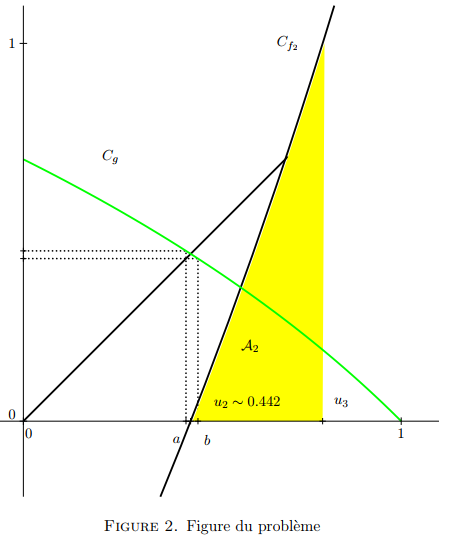
On peut donc prendre $n = 9 \text{ et } a_9 ≡ 0.442$.

3.  Voir la figure 2.

Source: Office du Bac