Corrigé du bac Maths, S Pondichéry juin 2000

Exercice 1 4 points

Commun à  tous les candidats

Un professeur se trouve en possession de 5 clefs de salles. Il se tient devant une porte et il sait que, parmi ses 5 clefs, 2 n'ouvrent pas la porte parce qu'elles sont défectueuses mais les autres le peuvent. Il veut alors les tester toutes, une à  une. Le choix des clefs est effectué au hasard et sans remise. On appelle clef numéro $x$ la clef utilisée au $x$-ième essai.

1. On appelle $D_1$ l'évènement : " La clef numéro 1 n'ouvre pas la porte ". Calculer sa probabilité.

     On a bien sûr $p\left(D_1 \right) = \dfrac{2}{5}$.

2. On appelle $D_2$ l'évènement : " La clef numéro 2 n'ouvre pas la porte" . Calculer la probabilité que l'évènement $D_2$ se réalise, sachant que l'évènement $D_1$ est réalisé.

Si la clef numéro 1 n’a pas ouvert la porte il reste une clef défectueuse sur les quatre encore à essayer, donc $p_{D_1}\left(D_2 \right) = \dfrac{1}{4}$.

En déduire la probabilité de l'évènement $D_1\cap D_2$.

On a $p\left(D_1\cap D_2 \right) = p\left(D_1 \right)\times p_{D_1}\left(D_2 \right) = \dfrac{2}{5} \times \dfrac{1}{4} = \dfrac{1}{10}$.
On pourra, pour la suite de l'exercice, s'aider d'un arbre pondéré.

3. Quelle est la probabilité de l'évènement : " Les clefs numéros 1 et 2 ouvrent la porte et la clef numéro 3 ne l'ouvre pas" ?

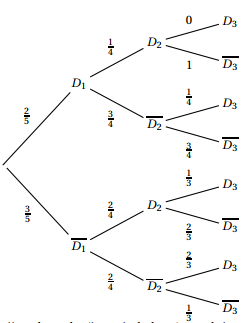
En suivant la septième branche (à partir du haut), on obtient :

$p\left(\overline{D_1}\cap \overline{D_2}\cap D_3 \right) = \frac{3}{5} \times \frac{2}{4} \times\frac{2}{3}  = \frac{2}{10} = \frac{1}{5} =  0,2$.

4. Pour $1 \leqslant i < j \leqslant 5$, on note $(i~;~j)$ l'évènement : " Les clefs qui n'ouvrent pas la porte sont les clefs numéros $i$ et $j$ ", et $P(i~;~j)$ la  probabilité de cet évènement.

    
        a. En suivant la troisième branche Calculer $P(2~;~4)$.
 $P(2~;~4) = p\left(\overline{D_1} \cap D_2 \cap \overline{D_3} \cap D_4 \cap \overline{D_5} \right) = \frac{3}{5} \times \frac{2}{4} \times\frac{2}{3} \times \frac{1}{2} = \frac{3 \times 2 \times2 \times1}{5\times 4\times 3} = \frac{1}{10} = 0,1$
        b. Calculer $P(4~;~5)$.
Si les clefs qui n'ouvrent pas sont les deux dernières, c'est que les trois premières ouvrent, donc :
$P(4~;~5) = p\left(\overline{D_1}\cap \overline{D_2}\cap \overline{D_3} \right) = \frac{3}{5} \times \frac{2}{4} \times\frac{1}{3} = \dfrac{1}{10}$.

Exercice 2 5 points

Candidats n'ayant pas choisi l'enseignement de spécialité}

Le plan complexe est muni d'un repère orthonormal direct $(\text{O},\overrightarrow{u},\overrightarrow{v})$ ; unité graphique 4~cm.
 
On appelle B le point d'affixe i et M$_1$ le point d'affixe :

$$z_1 = \dfrac{\sqrt{3} - 1}{2}(1 - \text{i}).$$

1. Déterminer le module et un argument de $z_1$.

On a $\left|z_1 \right|^2 = \left(\dfrac{\sqrt{3} - 1}{2} \right)^2 + \left(- \dfrac{\sqrt{3} - 1}{2} \right)^2 = \dfrac{1}{4}\left[\left(\sqrt{3} - 1 \right)^2  + \left(\sqrt{3} - 1 \right)^2\right]$

$= \dfrac{1}{4}\left[2\left(\sqrt{3} - 1 \right)^2\right] = \dfrac{2}{4} \left(\sqrt{3} - 1 \right)^2$.

Donc $\left|z_1 \right| = \dfrac{\sqrt{2}}{2}\left(\sqrt{3} - 1 \right)$.

On peut écrire en factorisant ce module :

$z_1 = \dfrac{\sqrt{2}}{2}\left(\sqrt{3} - 1 \right)\left(\frac{\sqrt{2}}{2} - \text{i}\frac{\sqrt{2}}{2} \right)= \dfrac{\sqrt{2}}{2}\left(\sqrt{3} - 1 \right)\left(\cos - \frac{\pi}{4} + \text{i}\sin - \frac{\pi}{4}\right)$

$=\dfrac{\sqrt{2}}{2}\left(\sqrt{3} - 1 \right)\text{e}^{-\text{i}\frac{\pi}{4}}$.

2. Soit M$_2$ le point d'affixe $z_2$, image de  M$_1$ par la rotation de centre O et d'angle $\dfrac{\pi}{2}$.

 Déterminer le module et un argument de $z_2$.

On sait que l'écriture complexe de la rotation est $z \longmapsto z\text{e}^{\text{i}\frac{\pi}{2}}$ ou simplement $z \longmapsto \text{i}z$.

Donc $z_2 =  \text{i}z_1 = \text{e}^{\text{i}\frac{\pi}{2}}\left[\dfrac{\sqrt{2}}{2}\left(\sqrt{3} - 1 \right)\text{e}^{-\text{i}\frac{\pi}{4}} \right]= \dfrac{\sqrt{2}}{2}\left(\sqrt{3} - 1 \right)\text{e}^{\text{i}\frac{\pi}{4}}$.

Donc $\left|z_2\right| = \left|z_1\right| = \dfrac{\sqrt{2}}{2}\left(\sqrt{3} - 1 \right)$ et un argument de $z_2$ est $\dfrac{\pi}{4}$.

Montrer que le point M$_2$ est un point de la droite $(D)$ d'équation $y = x$.
Comme un argument est égal à $\dfrac{\pi}{4}$ la partie réelle est égale à la partie soit $x = y$ imaginaire, soit $x = y$. Donc  M$_2$ est un point de la droite $(D)$ d'équation $y = x$.

3.  Soit M$_3$ le point d'affixe $z_3$, image de M$_2$ par l'homothétie de centre O et de rapport $\sqrt{3} + 2$.

    a. Montrer que $z_3 = \dfrac{\sqrt{3} + 1}{2} (1 + i).$

Par définition de l'homothétie, on a $z' = \left(\sqrt{3} + 2 \right)z$.

Donc $z_3 =  \left(\sqrt{3} + 2 \right)z_2 = \left(\sqrt{3} + 2 \right)\times \left[\dfrac{\sqrt{2}}{2}\left(\sqrt{3} - 1 \right)\text{e}^{\text{i}\frac{\pi}{4}}\right]$

$= \left(\sqrt{3} + 2 \right)\times \left[\dfrac{\sqrt{2}}{2}\left(\frac{\sqrt{2}}{2} + \text{i}\frac{\sqrt{2}}{2}\right)\right] = \dfrac{\sqrt{3} + 1}{2} (1 + i)$.
        b. Montrer que les points M$_1$ et M$_3$ sont situés sur le cercle de centre B et de rayon $\sqrt{2}$.
On a $\text{B}M_1^2 = \left|\dfrac{\sqrt{3} - 1}{2}(1 - \text{i}) - \text{i} \right|^2 =  \left|\dfrac{\sqrt{3} - 1}{2} -  \text{i}\dfrac{\sqrt{3} + 1}{2} \right|^2 = \dfrac{\left(\sqrt{3} - 1 \right)^2}{4} + \dfrac{\left(\sqrt{3} + 1 \right)^2}{4}$

$= \dfrac{+3 + 1 - 2\sqrt{3} + 3 + 1 + 2\sqrt{3}}{4} = \dfrac{8}{4} = 2$, donc $\text{B}M_1 = \sqrt{2}$.
        
$\text{B}M_3^2 = \left|\dfrac{\sqrt{3} + 1}{2}(1 + \text{i}) - \text{i} \right|^2 =  \left|\dfrac{\sqrt{3} + 1}{2} -  \text{i}\dfrac{\sqrt{3} + 1}{2} \right|^2 = \dfrac{\left(\sqrt{3} + 1 \right)^2}{4} + \dfrac{\left(\sqrt{3} + 1 \right)^2}{4}$

$= \dfrac{+3 + 1 + 2\sqrt{3} + 3 + 1 - 2\sqrt{3}}{4} = \dfrac{8}{4} = 2$, donc $\text{B}M_3 = \sqrt{2}$.

Les points M$_1$ et M$_3$ sont situés sur le cercle de centre B et de rayon $\sqrt{2}$.

4. Construire, à  la règle et au compas, les points M$_1$,~ M$_2$ et M$_3$ en utilisant les questions précédentes ; on précisera les différentes étapes de la construction.

Soit A le point d'affixe 1. le triangle OAB est rectangle isocèle et AB $= \sqrt{2}$. On a donc le rayon du cercle de centre qui contient les points $M_1$ et $M_3$. Le point $M_1$ est sur la bissectrice des axes d'équation $y = - x$ et $M_3$ sur la bissectrice des axes d'équation $y = x$.

Enfin $M_2$ est lui aussi sur la première bissectrice et tel que O$M_2 = \text{O}M_1$.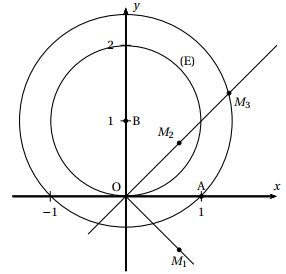

 

5.  À tout point $M$ du plan d'affixe $z$ (distinct de B), on associe le point $M'$, d'affixe $Z$ telle que $Z = \dfrac{1}{\text{i} - z}$.

Déterminer et construire l'ensemble (E) des points $M$ du plan ($M$ distinct de B) tels que $M'$ appartienne au cercle de centre O et de rayon 1.
On a $\text{O}M' = |Z| = \left| \dfrac{1}{\text{i} - z}\right| = \dfrac{1}{|\text{i} - z|} = \dfrac{1}{\text{B}M}$.

Donc $\text{O}M' = 1 \iff \dfrac{1}{\text{B}M} = 1 \iff \text{B}M = 1$.

L'ensemble (E) est donc le cercle de centre B et de rayon 1.

 

Exercice 2 5 points

Candidats ayant choisi l'enseignement de spécialité

Dans tout l'exercice, $n$ désigne un entier naturel non nul.

1.     

        a. ~Pour $1 \leqslant n \leqslant 6$, calculer les restes de la division euclidienne de $3^n$ par 7.
$$\begin{array}{|c|c|c|c|c|c|c|} \hline n&1&2&3&4&5&6\\\hline 3^{n}&1&9&27&81&243&729\\\hline \text{Reste}&3&2&6&4&5&1\\\hline \end{array}$$     

Or $72 = 700 + 28 = 7 \times 100 + 7\times 4 = 7\times (100 + 4) = 7\times 104$.
        b. Démontrer que, pour tout $n,\: 3^{n + 6} - 3^n$ est divisible par 7.        
En déduire que $3^n$ et $3^{ n + 6}$ ont le même reste dans la division par 7.
$3^{n + 6} - 3^n = 3^n \times 3^6 - 3^n = 3^n\left(3^6 - 1\right) = 3^n(729 - 1) = 728\times 3^n$.

728 et par conséquent $3^{n + 6} - 3^n$ est multiple de 7 pout tout naturel.
        c. À l'aide des résultats précédents, calculer le reste de la division euclidienne de $3^{1000}$ par 7.
On a ${1000} = 6 \times 166 + 4$, donc d'après le résultat précédent les nombres $3^{{1000}},\:3^{{1000} - 6},\:3^{{1000} - 2\times 6},\:\ldots,\:3^{{1000} - 6\times 166}$ ont le même reste dans la division par 7.

Mais $3^{{1000} - 6\times 166} = 3^4$ qui a d'après la première question comme reste $4$.
 
        d. De manière générale, comment peut-on calculer le reste de la division euclidienne de $3^n$ par 7, pour $n$ quelconque ?
Pour $n$ quelconque : $n = 6n' + r$ avec $0\leqslant r \leqslant 5$  ; le reste de la division de $n$ par 7 est le même que le reste de la division par de $3^r$ par 7

Si $r = 0$, le reste de la division par 7 est le même que le reste de la division par 7 de $3^6$, soit d'après la première question : 1. Or 1 est le reste de la division de  $3^0$ par 7.

Dans tous les cas le reste de la division euclidienne de $3^n$ par 7, pour $n$ quelconque est égal au reste de la division par de $3^r$ où $r$ est le reste de la division euclidienne de $n$ par 6.        
        e. En déduire que, pour tout entier naturel $n, 3^n$ est premier avec 7.
D'après les résultats a. et d., pour $n \ne 0$,
        
$3^n = 7q + r$, avec $1\leqslant r \leqslant 6$.

$3^n$ n'est donc pas multiple de 7 qui est premier, donc $3^n$ est premier avec 7.

2.  Soit $U_n = 1 + 3 + 3^2 + \cdots + 3^{n-1} = \displaystyle\sum_{i=0}^{i=n-1} 3^i$, où $n$ est un entier naturel supérieur ou égal à 2.

        a Montrer que si $U_{n}$ est divisible par 7, alors $3^n - 1$ est divisible par 7.

$U_n$ est la somme des termes d'une suite géométrique de premier terme 1 et de raison 3, donc :

$U_n = \dfrac{3^n - }{3  - 1} = \dfrac{3^n - 1}{2}$.

Comme $U_n$ est une somme d'entiers, c'est un entier, donc $3^n - 1$ est multiple de 2.

$3^n - 1 = 2U_n$. Donc si $U_n$ est divisible par 7, alors $3^n - 1$ est divisible par 7.
        b. Réciproquement, montrer que si $3^n - 1$ est divisible par 7, alors $U_n$ est divisible par 7.
En déduire les valeurs de $n$ telles que $U_n$ soit divisible par 7.
D'après le calcul précédent, si  $3^n - 1$ est divisible par 7, alors $2U_n$ est aussi divisible par 7 ; mais 7 et 2 sont des entiers premiers, donc premiers entre eux ; d'après le théorème de Gauss $U_n$ est divisible par 7.

On a vu que quand $U_n$ est multiple de 7, $3^n - 1$ l'est aussi ; ceci est réalisé quand le reste de la division de $3^n$ par 7 est égal à 1, donc si $n$ est un multiple de 6.

Dernier exemple du tableau $3^6 - 1 = 729 - 1 = 728 = 7\times 104$.

Problème 11 points}

Partie A

$\star$ Étude de la fonction $g ~: ~x \mapsto \ln\left(\dfrac{3 + x}{3 - x}\right)$

Soit la fonction $g$ définie sur $]- 3~;~3[$ par : $g(x) = \ln\left(\dfrac{3 + x}{3 - x}\right)$.

1.  Étudier la parité de la fonction $g$.

Sur $]- 3~;~3[$, $g(- x) = \ln\left(\dfrac{3 - x}{3 + x}\right) = \ln (3 - x) - \ln (3 + x) = -\left[\ln (3 + x)  - \ln (3 - x) \right]$

$= \ln\left(\dfrac{3 + x}{3 - x}\right) = g(x)$ : la fonction $g$ est paire sur l'intervalle $]- 3~;~3[$.

2.  

        a. Calculer les limites de $g$ en $- 3$ et en $3$.
On a $\displaystyle \lim_{x \to - 3} (3 - x) = 6$ et $\displaystyle \lim_{x \to - 3}3 + x = 0$, donc $\displaystyle \lim_{x \to - 3}g(x) = - \infty$.

De même $\displaystyle \lim_{x \to  3} (3 - x) = 0$ et $\displaystyle \lim_{x \to - 3}(3 + x) = 6$, donc $\displaystyle \lim_{x \to - 3}g(x) = + \infty$.    
        b. Étudier le sens de variation de $g$ sur [0~;~3[.
Sur $[0~;~3[$, $g$ est dérivable et en posant :$\dfrac{3 + x}{3 - x} = u$

$g'(x) = \dfrac{u'}{u}$

Or $u'(x) = \dfrac{3 - x + (3 + x)}{(3 - x)^2} = - \dfrac{6}{(3 - x)^2}$.

D'où $g'(x) = \dfrac{dfrac{6}{(3 - x)^2}}{\frac{3 + x}{3 - x}} = \dfrac{6}{(3 + x)(3 - x)} = \dfrac{6}{9 - x^2}$.

Or $- 3 < x < 3 \Rightarrow 0 < x^2 < 9 \iff 9 - x^2 > 0$.

La dérivée quotient de termes positifs est positive : la fonction $g$ est croissante de moins l'infini à plus l'infini et $f(0) = \ln \frac{3}{3} = \ln 1 = 0$.        
Dresser son tableau de variation sur $]- 3~;~3[$.

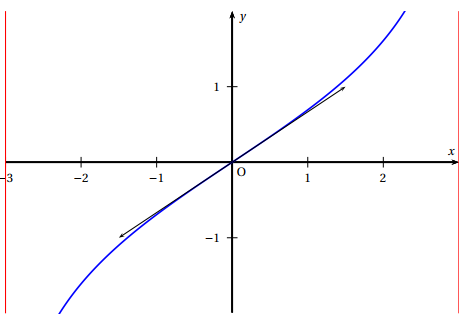
3.  Soit $(\text{O},\overrightarrow{\imath},\overrightarrow{\jmath}$ un repère orthonormal d'unité graphique 4 centimètres. Soit ($\mathcal{C}$) la courbe représentative de la fonction $g$ dans ce repère.

        a. Déterminer une équation de la tangente ($T$) à  ($\mathcal{C}$) au point d'abscisse 0.
        Une équation de  ($T$) à  ($\mathcal{C}$) au point d'abscisse 0 est :  
        $y - g(0) = g'(0)(x - 0)$ ; comme $g'(0) = \dfrac{6}{9} = \dfrac{2}{3}$, l'équation s'écrit :     
        $y - 0 = \dfrac{2}{3}(x - 0)$ soit $y = \dfrac{2}{3}x$.
        b. Tracer dans le repère la courbe ($\mathcal{C}$) et sa tangente ($T$).

4.  Étudier le signe de $g(x)$ suivant les valeurs de $x$.

D'après les variations de $g$, on a $g(x) < 0$ sur $]- 3~;~0[$, $g(x) > 0$ sur $]0~;~3[$ et $g(0) = 0$.

5.  

        a. Calculer la dérivée de la fonction $x \mapsto xg(x)$.
Si $h(x) = xg(x)$, alors $h'(x) = g(x) + xg'(x) = \ln\left(\dfrac{3 + x}{3 - x}\right) + \dfrac{6x}{(3 + x)(3 - x)}$.        
        b. Calculer l'aire, exprimée en cm$^2$, de la portion de plan délimitée par la courbe ($\mathcal{C}$), l'axe des abscisses et les droites d'équations $x = 0$ et $x = 1$. On donnera la valeur exacte de cette aire, puis une valeur approchée au mm$^2$ près.
        L'aire en unité d'aire de la portion de plan délimitée par la courbe ($\mathcal{C}$), l'axe des abscisses et les droites d'équations $x = 0$ et $x = 1$ est égale à l'intégrale :     
$$\displaystyle\int_0^1 g(x) \:\text{d}x, \quad \text{car sur\:} [0~;~1], \: g(x) \geqslant 0$$

Or d'après la question 5. a. : $\left[xg\right]'(x) = g(x) + xg'(x)$ ou $g(x) = \left[xg\right]'(x) - xg'(x) = \left[xg\right]'(x) - \dfrac{6x}{9 - x^2}$.

Or $\dfrac{- 6x}{9 - x^2} = 3 \times \dfrac{-2x}{9 - x^2}$ qui est de la forme $\dfrac{u'(x)}{u(x)}$ qui est la dérivée de $3\ln \left(9 - x^2\right)$.

Finalement $g(x)$ est donc égale à la différence de deux dérivées ou encore à la dérivée de la différence et on peut donc calculer 

$\displaystyle\int_0^1 g(x) \:\text{d}x = \displaystyle\int_0^1 \left[ (xg(x)) -  \left(3\ln \left(9 - x^2\right)\right)\right]-(\:\text{d}x = \left[xg(x) + 3\ln \left(9 - x^2\right)\right]_0^1 = \ln 2 + 3\ln 8 - 3\ln 9 = \ln 2 + 9\ln 2 - 6\ln 3 = 10\ln 2 - 6\ln 3$.

L'unité étant égale à 4~cm sur chaque axe, l'unité d'aire est égale à $4 \times 4 = 16$~cm$^2$.

L'aire en cm$^2$ de la portion de plan délimitée par la courbe ($\mathcal{C}$), l'axe des abscisses et les droites d'équations $x = 0$ et $x = 1$ est donc égale à

$16(10\ln 2 - 3\ln 3) \approx 5,44$~cm$^2$.

Partie B

$\star$ Étude d'une courbe paramétrée

Le plan est rapporté à  un repère orthonormal $(\text{O},\overrightarrow{\imath},\overrightarrow{\jmath})$ d'unité graphique 4~centimètres.

Soit la courbe paramétrée ($\Gamma$) définie par :
$$\left\{ \begin{array}{r c l} x(t) & = & t\left(3 - t^2\right)\\ y(t) & = & tg(t) \end{array}\right. \quad \text{pour}\quad t \in [-2~;~2].$$
où $g$ désigne la fonction étudiée dans la partie A. On note $M(t)$ le point de coordonnées
$(x(t)~;~y (t))$.  
        a. Comparer d'une part $x(t)$ et $x(- t)$ et d'autre par $y(t)$ et $y(- t)$.
$x(- t) = -t\left(3 - (-t)^2\right) = - t\left(3 - t^2\right) = - x(t)$ : $x$ est impaire.
$y(- t) = - tg(- t) = tg(t) = y(t)$ : $y$ est paire.
        b. Par quelle transformation peut-on passer de $M(t)$ à  $M(- t)$ ?
Les points     $M(t)$ et  $M(- t)$ ont la même ordonnée et des abscisses opposées : ils sont donc symétriques autour de l'axe des ordonnées qui est un axe de symétrie de ($\Gamma$).    
En déduire que ($\Gamma$) admet un axe de symétrie que l'on précisera.

2.  Étudier la fonction $x ~:~ t \mapsto t \left(3 - t^2\right)$ et dresser son tableau de variations sur [0~;~2].

$x$ est dérivable et sur $[-2~;~2]$, $x'(t) = 3 - (t)^2 - 2t \times t =  3 - 3t^2 = 3\left( 1 - t^2\right) = 3(1 + t)(1 - t)$ qui est du signe de $(1 + t)(1 - t)$ :

$\bullet~~$si $t \in ]- 1~;~1[,\:(1 + t)(1 - t) > 0$ et $x't() > 0$ ; la fonction $x$ est croissante sur  $]- 1~;~1[$ ;

$\bullet~~$si $t \notin ]- 1~;~1[,\:(1 + t)(1 - t) < 0$ et $x't() > 0$ ; la fonction $x$ est décroissante sur  $]- 2~;~- 1[$ et sur $]1~;~2]$.

3. En utilisant la partie A.}, montrer que la fonction

$t \mapsto y(t)$ est strictement croissante sur l'intervalle [0~;~2].

$y$ est dérivable sur $]-2~;~2[$ et sur cet intervalle :

$y'(t) = g(t) + tg'(t) = g(t) + \dfrac{6t}{9 - t^2}$.

Sur $]-2~;~2[$, \:$9 - t^2> 0$ ; le signe de $y'(t)$ dépend donc de $t$ et de $g(t)$.

On a vu dans  la partie A que pour $t < 0,\:g(t) < 0$ et comme  $\dfrac{6t}{9 - t^2} < 0$, on a $y'(t) < 0$ sur $]-2~;~0[$.

De même si $t > 0$, on a vu que $g(t) > 0$ et comme $\dfrac{6t}{9 - t^2} > 0$, on a $y'(t) > 0$ sur $]0~;~2]$.

$y$ est donc décroissante sur $]-2~;~0[$ et croissante sur  $]0~;~2]$.

4. Dresser le tableau des variations conjointes des fonctions

$t \mapsto x(t)$ et $t \mapsto y(t)$ sur [0~;~2].
On peut donc dresser le tableau des variations conjointes des fonctions
$t \mapsto x(t)$ et $t \mapsto y(t)$ sur [0~;~2] :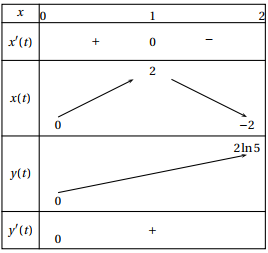

5. Pour quelles valeurs de $t$ l'abscisse de $M(t)$ est-elle nulle ?

$x(t) = 0 \iff t\left(3 - t^2\right) = 0 \iff \left\{\begin{array}{l c l} t&=&0\\ 3 - t^2&=&0 \end{array}\right. \iff \left\{\begin{array}{l c l} t&=&0\\ t&=&\sqrt{3}\:\text{ou}\\ t&=&- \sqrt{3} \end{array}\right.$

Préciser alors les ordonnées des points correspondants de ($\Gamma$).
On a $M(0)(0~;~0)$ ; $M\left(\sqrt{3}\right)\left(\sqrt{3}~;~y\left(\sqrt{3} \right)\right)$.

Or $y\left(\sqrt{3} \right) = \sqrt{3}g\left(\sqrt{3} \right) = \sqrt{3} \times \ln \left(\dfrac{3 + \sqrt{3}}{3 - \sqrt{3}} \right) = \sqrt{3}\ln \left(\dfrac{\left(3 + \sqrt{3} \right)\left(3 + \sqrt{3} \right)}{\left(3 + \sqrt{3} \right)\left(3 - \sqrt{3} \right)} \right) = \sqrt{3}\ln \left(\dfrac{9 + 3 + 6\sqrt{3}}{9 - 3}\right) = \sqrt{3}\ln \left(2 +  \sqrt{3}\right)$.

Donc  $M\left(\sqrt{3}\right)\left(\sqrt{3}~;~\sqrt{3}\ln \left(2 +  \sqrt{3}\right)\right)$.

Enfin $M\left(-\sqrt{3}\right)\left(- \sqrt{3}~;~\sqrt{3}\ln \left(2 +  \sqrt{3}\right)\right)$ car ce point et le précédent sont symétriques autour de l'axe des ordonnées.

6.  Tracé de ($\Gamma$)

        a. Placer, dans le repère $(\text{O},\overrightarrow{\imath},\overrightarrow{\jmath})$, les points
M(0), M(1), M$\left(\sqrt{3}\right)$ et M(2) qui correspondent respectivement aux valeurs 0, 1, $\sqrt{3}$ et 2 du paramètre $t$.
Voir la figure avec $M(1)(2~;~\ln 2)$.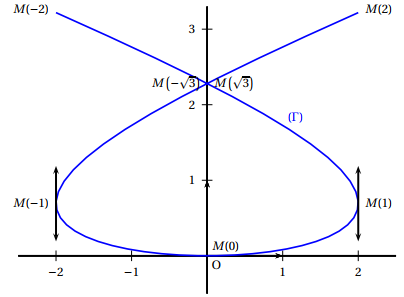

 
        b. Préciser un vecteur directeur des tangentes à  ($\Gamma$) aux points M(0) et M(1) et tracer ces tangentes.
En $M(0)$ le vecteur directeur de la tangente a pour coordonnées (3~;~0) et en $M(1)$ le vecteur directeur  a pour coordonnées $\left(0~;~\ln 2 + \frac{3}{4}\right)$.        
        c: Tracer ($\Gamma$).
Voir ci-dessus.

 

Source: www.apmep.fr